基于Fast-ICA的CDMA信号扩频序列盲估计及性能分析

陆凤波，黄知涛，姜文利

（国防科技大学 电子科学与工程学院，湖南 长沙 410073）

1 引言

DS-CDMA（direct sequence code division multiple access）系统具有多址通信、低截获概率、抗干扰能力强等优点，在通信、测控及导航等领域有着越来越多的应用。DS-CDMA可分为长码（long-code）和短码（short-code）扩频2种扩频方式，对于SC-DS-CDMA信号，扩频序列周期等于信息符号周期，对于LC-DS-CDMA信号，扩频序列周期大于信息符号周期，信息符号速率可以根据实际需要灵活选择，因此得到了广泛的实际应用。在非合作通信以及通信侦察中，如果接收方未知目标用户的扩频序列，就无法对接收信号进行解调并获取传输的信息，因此对DS-CDMA信号的扩频序列进行盲估计具有十分重要的意义。

目前，对DS-CDMA信号扩频序列盲估计的相关研究主要是针对SC-DS-CDMA信号。Yao Yingwei等人提出了基于EM的SC-DS-CDMA信号盲估计算法[1]；Afshin Haghighat等人提出一种基于MUSIC的同步SC-DS-CDMA信号扩频序列盲估计方法[2～4]；Nzéza等人提出了基于 F 范数和特征结构分析的扩频序列估计方法[5,6]，能够完成非同步SC-DS-CDMA 信号的扩频序列估计；T. Koivisto等人首先对接收信号中的某一用户进行盲同步，然后通过逐次提取的方法依次估计出所有用户的扩频序列[7]；由于CDMA信号每个用户的信息序列和扩频序列是相互独立的，且每个用户的扩频序列具有周期性，可以利用独立分量分析[8]完成多用户扩频序列的盲分离，付卫红等人把观测信号表示成盲源分离的表达形式，提出了基于盲源分离的SC-DSCDMA信号扩频序列盲估计算法[9]。由于 LC-DSCDMA信号在一个扩频周期内有多个信息符号，扩频序列估计比短码的情况更为复杂，上述方法都不适用于长码扩频CDMA信号。

针对 LC-DS-CDMA信号扩频序列盲估计问题，本文提出了一种基于Fast-ICA（fast independent component analysis）的DS-CDMA信号扩频序列盲估计算法，先把接收信号分成若干重叠的片段，再用Fast-ICA方法估计出每个用户的扩频序列片段，然后利用重叠部分的相关性解决每个用户扩频序列的次序置换和幅度模糊问题，最后通过拼接得到每个用户完整周期的扩频序列。该方法不仅能适用于LC-DS-CDMA信号，而且对同步LC-DS-CDMA信号也同样适用。理论分析和仿真结果验证了本文方法的有效性。

2 DS-CDMA信号模型

假设 DS-CDMA信号的用户总数为M，则接收机接收到的信号为

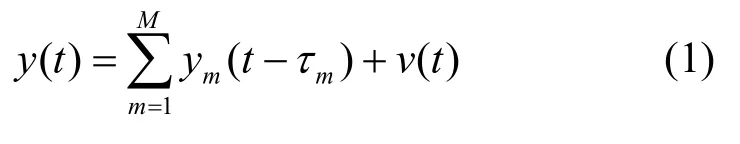
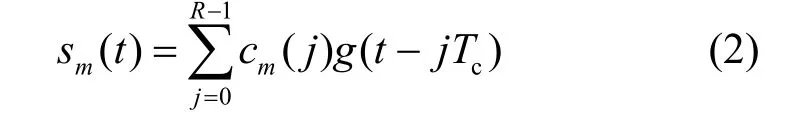
其中，Tc为扩频码码片周期， R=T Tc为扩频序列位数，｛cm( j) ｝为第m个用户的扩频序列，g(t)表示持续时间为Tc且具有单位能量的码片波形。扩频增益P =TsTc，当P＜R时，为LC-DS-CDMA信号，当P=R时，为SC-DS-CDMA信号。在接收端先使信号y(t)通过匹配滤波器 h (t)=g (Tc- t)，再用码片速率进行采样，则接收信号的离散形式可以表示为

1) 用户信息序列｛bm( i)｝是随机的，且不同用户的信息序列是不相关的；

2) 对于长码扩频信号，扩频序列长度 R与扩频增益P之比为非整数；

3) CDMA信号的周期数目N大于等于用户数目M。上述3个假设条件在实际的DS-CDMA系统中一般都能够得到满足。

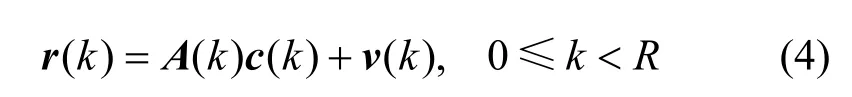
把DS-CDMA信号的每个扩频周期都看作一个阵元接收到的信号，则式（3）可以表示成矩阵形式：号表示向下取整。对于LC-DS-CDMA信号，由于一个扩频周期内包含有多个信息符号，则当0≤k＜R时，混合矩阵A(k)是时变的，不能直接用Fast-ICA的方法来完成扩频序列c(k)的估计。

可以把完整周期的扩频序列分成L个片段，使每个扩频序列片段的长度H远小于扩频增益P，由于扩频序列长度R与扩频增益P之比为非整数，对于任意第l个片段，当0kH＜≤时每个用户扩频序列片段对应的信息序列大多数不会发生跳变，发生信息跳变的观测可以当作噪声干扰，混合矩阵lA近似恒定。

由于通过盲分离恢复出的源信号的顺序和幅度存在不确定性，可以使相邻的2个片段相互重叠，利用重叠部分的相关性来解决次序和幅度模糊。信号重叠分段如图1所示。

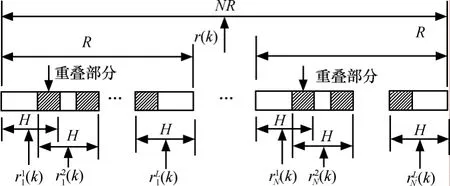
图1 LC-DS-CDMA信号重叠分段

令重叠长度为D，D˜=H-D，则第l个片段的接收信号r(k)可以表示为

其中，0≤k＜H，1≤l≤L，

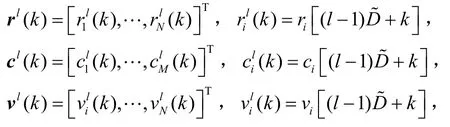
在扩频序列片段对应的时间内，混合矩阵 Al近似恒定，可以表示为

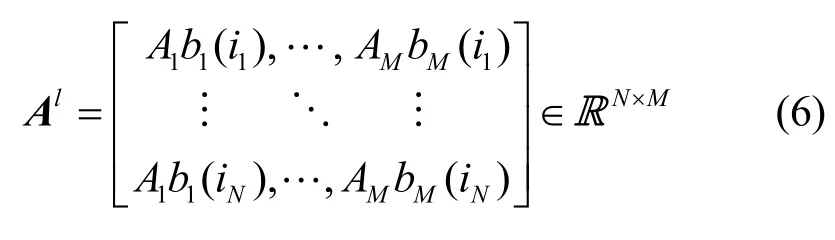
式（5）是一个典型的盲分离模型，估计每个用户的扩频序列片段就相当于从接收信号rl(k)中分离出源信号cl(k)。由于不同用户的扩频序列ci(k)是相互独立的，此外，由假设1和2可知混合矩阵Al是列满秩的，即 r ank ( Al) =M，满足独立分量分析的假设条件，可以利用 Fast-ICA算法来完成DS-CDMA信号的扩频序列估计。

通过Fast-ICA算法对式（5）中的扩频序列片段进行盲分离，能够得到L个相互重叠的扩频序列片段cˆl(k)(1 ≤ l≤L)，再通过重叠部分构造协方差矩阵来解决次序和幅度模糊问题，把L个扩频序列片段拼接成完整的扩频序列cˆ(k)。

3 基于Fast-ICA的盲分离算法

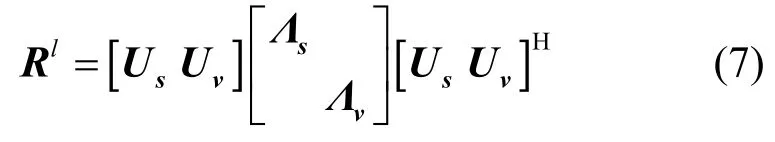
其中，Us和 Uv分别为信号子空间和噪声子空间。对观测信号rl进行白化，则白化后的信号zl为

其中，rl的维数为N，白化后的信号维数zl为M。下面估计分离矩阵 W =［w ,…,w］∈RM×M。由文献

1M[10]可知，首先为 wi设置一个初始向量，然后通过下式进行迭代，直到源信号收敛。

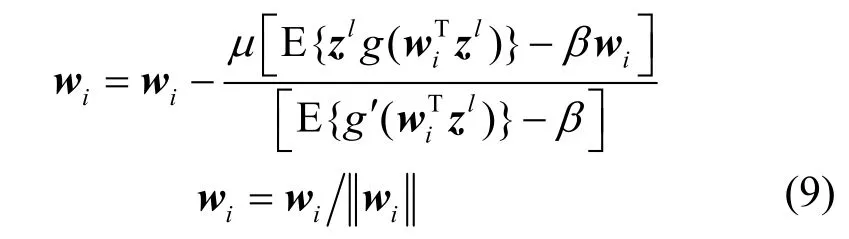
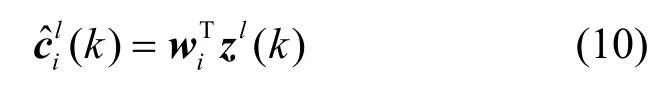
这样就可以完成第i个源信号的提取，为了能够完成M个源信号的提取，可以设置M个不同的初始值逐次提取出M个用户的扩频序列。但是为了保证每次提取出来的都是尚未提取过的信号，必须在重复下一次提取之前把已提取过的分量去掉，可以通过 Schmidt正交化来达到这一目的。如果已经提取出第 i个源信号，则在第i＋1个源信号提取之前，将第i个分离矢量 wi+1正交化

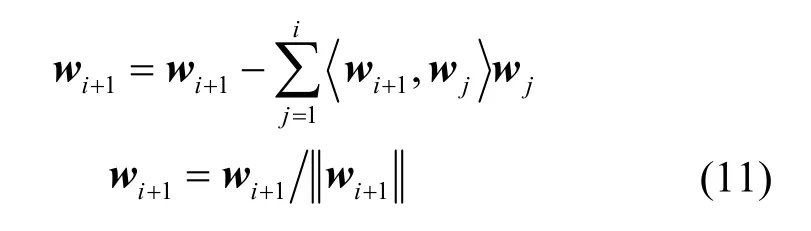
4 次序和幅度模糊

首先利用扩频序列的重叠部分来解决次序和幅度模糊问题，然后通过拼接完成整个扩频序列的估计。

令第l个扩频序列片段与第l + 1个扩频序列片段的重叠部分为 dl(k)和 dl+1(k ) (0 ≤ k ＜ D)，其中，dl(k )= [c ˆ1l(D ˜+ k ),…,cˆMl(D ˜ +k)]T，D˜=H-D，定义协方差矩阵R˜为只有一个元素为±1，其余元素都为零。考虑到噪声的影响，通过搜索矩阵R˜每一列（行）的绝对值的最大值位置来解决源信号的置换问题，即

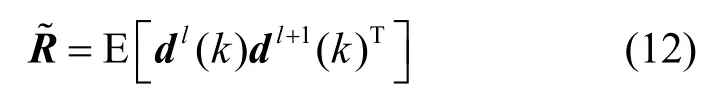
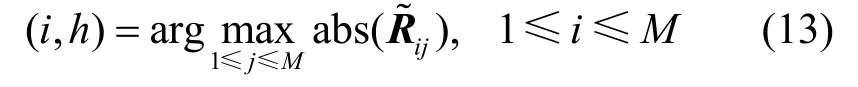
则第i个扩频序列片段与第h个扩频序列片段对应的是同一个用户。

由于通过盲分离估计出的信号幅度具有不确定性，可以通过 R˜ih的符号来判断第l个扩频序列片断与第l+1个扩频序列片段的相对极性，即

其中，sign(R ˜ih) 为符号函数。通过式(13)和式(14)就可以完成扩频序列片段cˆl和 cˆl+1的拼接。因此，通过计算L-1个协方差矩阵R˜就可以完成L个扩频序列片段的拼接，得到完整的扩频序列cˆ。

5 性能分析与仿真结果

5.1 性能分析

本文通过第 m个用户的扩频序列的输出信噪比SNRoutm来衡量第 m个用户的扩频序列的估计性能， S NRoutm的定义为

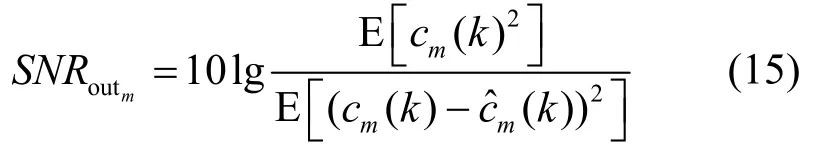
当每个用户的功率相等时，可以用平均输出信噪比SNRout来衡量整个DS-CDMA信号扩频序列估计性能，其中，，式（15）表明输出信噪比越高，扩频序列的估计性能越好。

文献[11]研究了在不考虑噪声条件下的Fast-ICA算法估计性能，第m个源信号sm(t)的输出信噪比 S NRoutm为

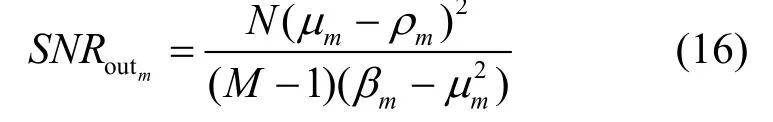
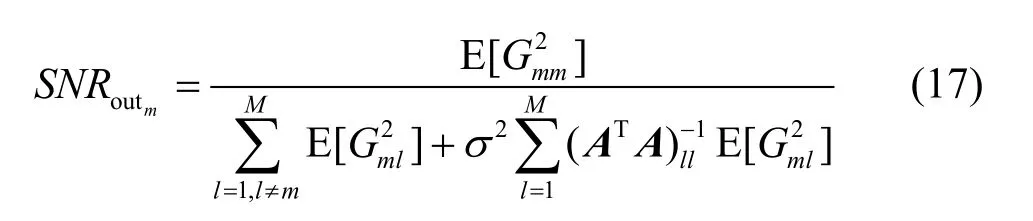
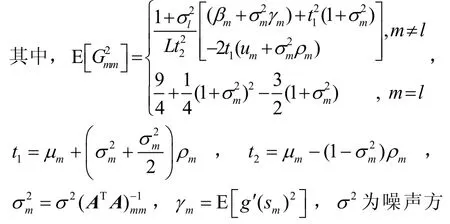
本文利用式（17）来分析 Fast-ICA算法恢复DS-CDMA信号扩频序列的性能。由式（4）可知，当P = R时，混合矩阵为

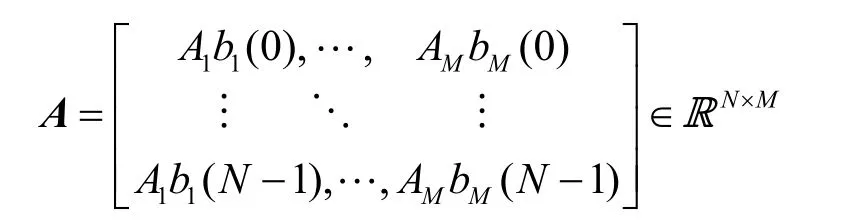
由于不同用户的信息序列｛bk(i )｝是不相关的，则

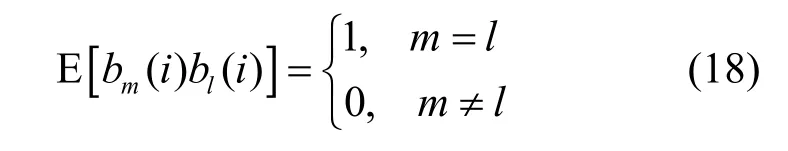
则矩阵 ( ATA)-1可以简化为

又因为扩频序列｛cm( i)｝是取值为±1的伪随机序列，非线性函数采用 g (u ) = u3，则

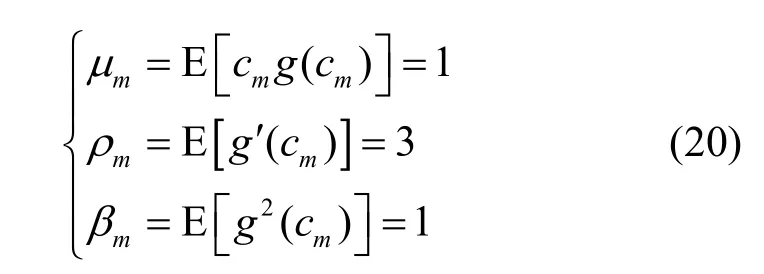
把式（19）和式（20）代入式（17），可得

5.2 仿真结果

下面通过5个仿真实验来验证理论分析的结果及本文算法的估计性能。其中，仿真实验1给出了不同用户数目时短码扩频信号扩频序列的估计性能以及通过式（22）得出的理论结果；仿真实验2、3、4分别给出了在不同分段长度、不同周期数目及每个用户功率不同条件下，LC-DS-CDMA信号扩频序列的估计性能；仿真实验 5给出了对于LC-DS-CDMA信号本文算法与文献[9]算法的性能比较。下列5个仿真实验中，第m个用户信号的信噪比 S NRm为 1 0lgAm2σ2。在每组仿真条件下，分别进行100次Monte-Carlo仿真。

仿真实验1 用户数M分别为2、4、6，每个用户的扩频序列为255bit的随机序列，扩频增益P为255，由于P = R，为SC-DS-CDMA信号，分段长度H为50，重叠长度 D = H -1，信号周期数目N为200，每个用户的功率相等，信噪比 S NRm变化范围为-15～40dB。

图2为不同用户数目条件下，SC-DS-CDMA信号扩频序列估计性能随信噪比变化曲线，从图中可以看出仿真结果与通过式（22）得出的理论结果一致（不同用户数目时得出理论结果几乎完全相同，因此图中只给出了一条理论曲线），此外，由于DS-CDMA信号的每个用户并不是严格相互正交的，随着用户数目的增多扩频序列的估计性能会略有下降。

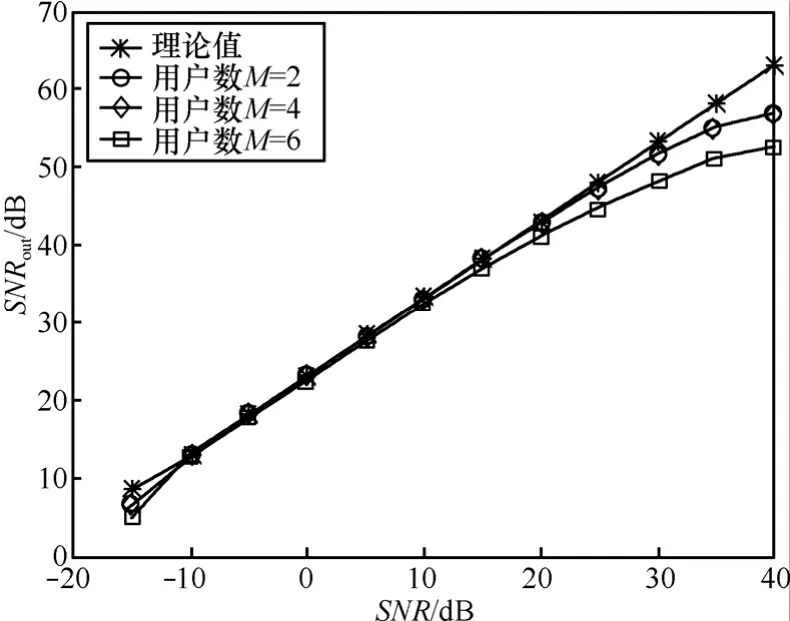
图2 SC-DS-CDMA信号扩频序列估计性能

仿真实验2用户数M分别为2、4、6，每个用户的扩频序列为255bit的随机序列，扩频增益P为 150。分段长度 H分别为 30和 50，重叠长度D =H -1，周期数目 N =200，每个用户的功率相等，信噪比 S NRm变化范围为-15～30dB。

图 3为用户数目不同、分段长度不同时，LC-DS-CDMA信号扩频序列估计性能随信噪比变化曲线，对于长码扩频信号，由于在每段的持续时间 H内信息符号可能会发生跳变，从而会形成干扰，因此扩频序列的估计性能明显低于短码扩频信号。当分段长度H较大时，信息符号发生跳变的概率变高，扩频序列的估计性能会降低。因此，分段长度H为30时的扩频序列估计性能高于分段长度H为50时的性能。从图中可以看出，当信噪比大于-10dB时，扩频序列的平均输出信噪比SNRout大于10dB，能够很好地恢复出每个用户的扩频序列。

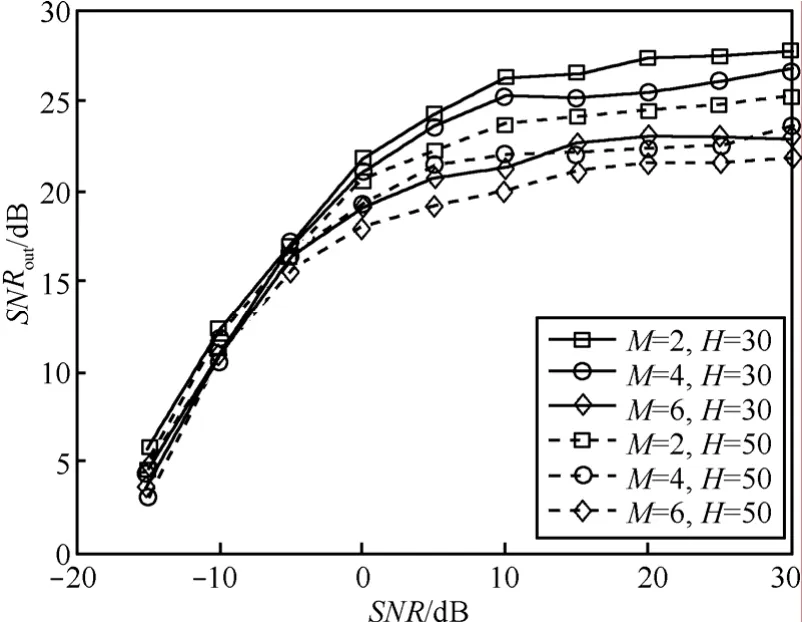
图3 LC-DS-CDMA信号扩频序列估计性能

仿真实验3 用户数目M分别为2、4、6，每个用户的扩频序列为255bit的随机序列，扩频增益P为150，。分段长度H为30，重叠长度 D=H -1，周期数N分别为50，100，200，400，每个用户的功率相等，信噪比 S NRm为-5dB。

图4为用户数目不同时，LC-DS-CDMA信号扩频序列估计性能随信号周期数目N变化曲线。从图中可以看出，周期数目N越多，扩频序列的估计性能越好。当周期数目增加1倍，估计性能大约提高3dB。

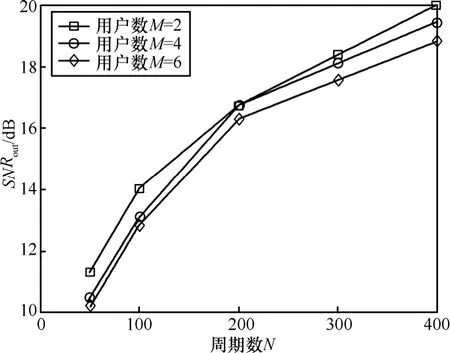
图4 扩频序列估计性能随周期数变化曲线

仿真实验4 用户数目M为3，每个用户的扩频序列为255bit的随机序列，扩频增益P为150，分段长度H为30，重叠长度 D = H -1，信号周期数目N为200，3个用户的功率比为4:2:1，功率最小用户的信噪比 S NR3变化范围为-15～20dB。

图 5为 3个用户功率比为 4:2:1时，LC-DSCDMA信号每个用户的扩频序列估计性能随 S NR3的变化曲线。从图中可以看出，当功率比不同时本文算法也能很好地估计出每个用户的扩频序列。用户 1的扩频序列估计信噪与用户 2的相比大约高3dB，用户2的信噪比比用户3的大约高3dB，这与每个用户的设置信噪比一致( S NR1= S NR2+3,SNR2= S NR3+3)。

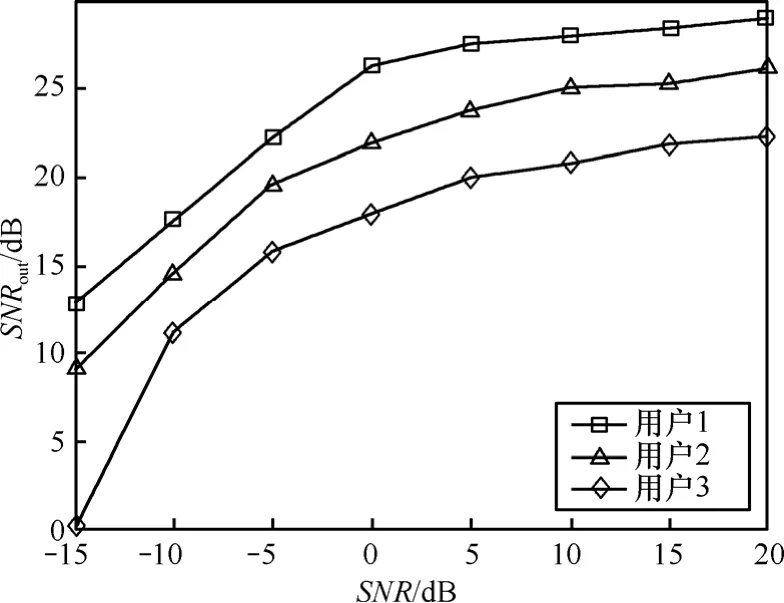
图5 各用户功率不等时扩频序列估计性能

仿真实验5 用户数目M分别为2、4，每个用户的扩频序列为255bit的随机序列，扩频增益P为100。分段长度H为30，重叠长度 D = H - 1，周期数N为200，每个用户的功率相等，信噪比 S NRm的变化范围为-10～30dB。

图6为用户数目不同时本文算法和文献[9]算法的估计性能。从图中可以看出，文献[9]中的算法估计出的扩频序列的输出信噪比小于5dB，此时对应的误码率大于 1 0-1，不能正确估计出LC-DS-CDMA信号的扩频序列，而本文算法的输出信噪比大于20dB，能够很好地估计出信号扩频序列。

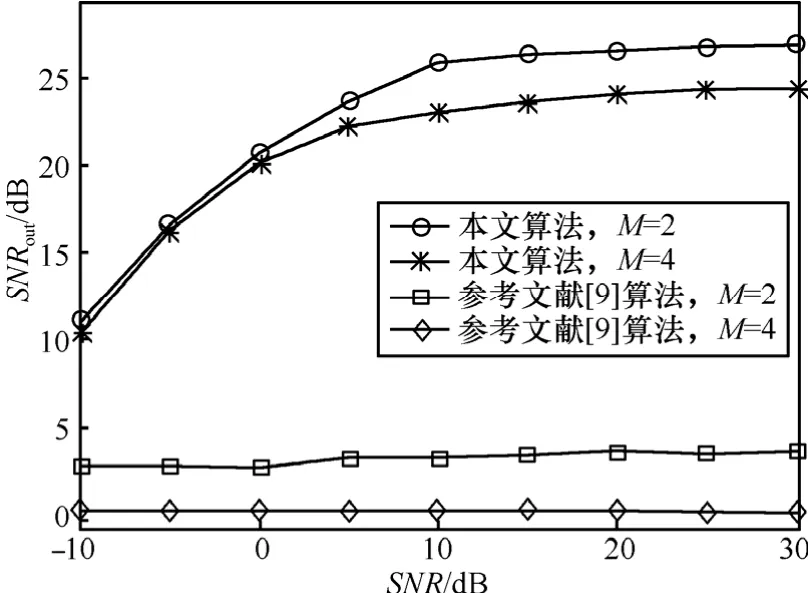
图6 本文算法与文献[9]算法性能比较

6 结束语

目前已有的DS-CDMA信号扩频序列盲估计算法不能适用于 LC-DS-CDMA信号，本文通过重叠分段的 Fast-ICA算法估计出每个用户的扩频序列片段，然后利用重叠部分的相关性解决扩频序列的次序和幅度模糊，从而得到完整周期的扩频序列，该方法既适用于LC-DS-CDMA信号，同时也能适用于同步 SC-DS-CDMA信号。理论分析和仿真结果验证了本文方法具有很好的估计性能。

[1] YAO Y W, POOR H V. Eavesdropping in the synchronous CDMA channel: an EM-based approach[J]. IEEE Transactions on Signal Processing, 2001, 49(8): 1748-1756.

[2] JOUTSENSALO J. Semi-blind CDMA code estimation in the downlink[A]. Proc of the 48th IEEE Vehicular Technology Conference[C]. Ottawa, Canada, 1998. 1356-1360.

[3] HAGHIGHAT A, SOLEYMANI M R. A MUSIC-based algorithm for spreading sequence discovery in multiuser DS-CDMA[A]. Pro of the 58th IEEE Vehicular Technology Conference[C]. Canada, 2003.978-981.

[4] HAGHIGHAT A, SOLEYMANI M R. A MUSIC-based algorithm for blind user identification in multiuser DS-CDMA[J]. EURASIP, 2005,5: 649-657.

[5] NZÉZA C N, GAUTIER R, BUREL G. Blind synchronization and sequences identification in CDMA transmissions[A]. Proc of the IEEE Military Communications Conference[C]. 2004. 1384-1390.

[6] NZÉZA C N, GAUTIER R, BUREL G. Parallel blind multiuser synchronization and sequences estimation in multirate CDMA transmissions[A]. Proc of the 40th Asilomar Conference on Signals, Systems and Computers[C]. Pacific Grove, 2006.2157-2161.

[7] KOIVISTO T, KOIVUNEN V. Blind despreading of short-code DS-CDMA signals in asynchronous multi-user systems[J]. Signal Processing, 2007, 87: 2560-2568.

[8] COMON P. Independent component analysis, a new concept?[J].Signal Processing, 1994, 36(3): 287-314.

[9] 付卫红, 杨小牛, 刘乃安. 基于盲分离的 CDMA多用户检测与伪码估计[J]. 电子学报, 2008, 36(7): 1319-1323.FU W H, YANG X N, LIU N A. The multi-user detection and chip sequence estimation for CDMA system based on the blind source separation[J]. Acta Electronica Sinica, 2008, 36(7): 1319-1323.

[10] HYVÄRINEN A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634, 1319-1323.

[11] TICHAVSKY P, KOLDOVSKY Z. Performance analysis of the Fast-ICA algorithm and Cramér-Rao bounds for linear independent component analysis[J]. IEEE Transactions on Signal Processing, 2006,54(4): 1189-1203.

[12] YANG X N, YAO J L, LI Z. Performance analysis of the Fast-ICA algorithm in ICA-based co-channel communication system[A]. Pro of the 5th International Conference on Wirless Communication, Network and Mobile Computing[C]. Beijing, China, 2009. 2055-2058.