GPS天线相位中心校正对低轨卫星精密定轨的影响研究

胡志刚,赵齐乐,郭 靖,刘经南

1.武汉大学测绘学院,湖北武汉430079;2.武汉大学卫星导航定位技术研究中心,湖北武汉430079

GPS天线相位中心校正对低轨卫星精密定轨的影响研究

胡志刚1,2,赵齐乐2,郭 靖1,2,刘经南2

1.武汉大学测绘学院,湖北武汉430079;2.武汉大学卫星导航定位技术研究中心,湖北武汉430079

执行各种低轨卫星任务的官方在公布定轨结果的同时并没有公布星载接收机的天线相位中心校正(PCV)信息,而PCV误差是星载 GNSS精密定轨必须考虑的主要误差源之一。以 GRACE卫星任务为例研究PCV误差对低轨卫星精密定轨的影响,利用 GPS观测数据直接估计与相位误差有关的天线相位偏差(PCO)和PCV参数,然后利用 K波段测距系统和卫星激光测距仪数据进行定轨评定。

天线相位中心校正;精密定轨;低轨卫星;天线;GPS

1 引 言

自美国成功研制GPS系统并投入运营以来,该系统以其全天候、全球分布、高精度定位定轨等优点已经渗透入各个应用领域并取得了很好的效果。精密定轨方面已取得一系列成绩,文献[1]利用GPS数据对CHAMP卫星进行精密定轨并获得了5 cm的定轨结果,文献[2]利用 GPS和DORIS系统得到Janson-1低轨卫星1 cm的高精度结果,文献[3]对孪星 GRACE进行了研究并获得径向1 cm,切向和法向3 cm的定轨结果。国内,文献[4]利用自主研究的 PANDA精密定轨软件对CHAMP卫星定轨也获得了径向切向法向2～3 cm定轨精度的可喜成果。高精度的定轨结果对于重力场的反演十分重要,2009年发射的GOCE卫星要求定轨结果为1 cm,这对精密定轨任务提出了更高的要求,迫使人们进一步对影响星载GNSS定轨精度的各种误差源进行深入研究。其中,对流层、电离层等可以通过模型或观测值组合较好地消除或削弱,剩下的主要误差包括观测噪声、天线相位中心变化(PCV)、多路径效应等。后两者误差很难通过观测值组合和作差的方式削弱,在精密定轨中常常被忽视。然而,文献[5—6]的研究表明 PCV的对定轨精度有明显影响,因此 PCV是星载 GNSS精密定轨必须考虑的主要误差源之一。遗憾的是搭载于低轨卫星上的GPS接收机不属于测地型接收机并且也没有这类天线的任何PCV改正信息。没有考虑PCV带来的误差影响必然会降低星载 GNSS精密定轨的精度。因此,本文就天线相位中心变化对低轨卫星精密定轨的精度影响进行了深入研究,并使用参数估计的方法直接估算天线相位中心PCV值,将 PCV误差从观测模型误差中分离出来。

2 天线相位中心校正方法

2.1 相位中心校正模型

GNSS相位观测值是通过测量卫星发射天线发射时刻相对于接收机接收时刻各自的瞬时相位中心得到[7-8]。然而其瞬时相位中心随着高度角、

方位角、卫星信号强度的变化而变化并且跟频率有关,在实际数据处理中无法得到卫星和接收机的瞬时相位中心的具体位置,因而引入一个平均相位中心来描述瞬时相位中心的平均值,该值相对于接收机参考点的差距称为天线相位偏差(PCO)。这样,如果将单个观测值的瞬时相位中心与平均相位中心相比较得到的偏差值就称为天线相位中心变化(PCV)。设PCO的矢量为a,卫星-接收机间的矢量为 r0,天线相位中心的改正模型由PCO和PCV两部分组成。

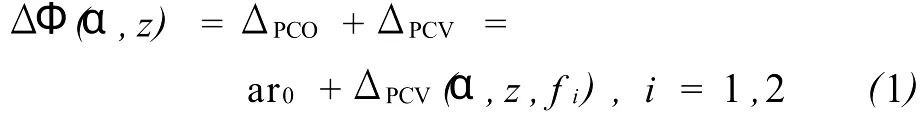
式中,α、z、fi分别为方位角、天顶距或高度角,信号频率;ΔPCV(α,z,f)为与方位角和高度角和频率有关的函数。

利用式(1)就实现了瞬时相位中心到天线参考点(ARP)的相位伪距近似改正。该式中的PCO矢量可以任意选取,但与其对应的PCV必须是自洽的。

2.2 LEO PCV估计方法

对于星载 GNSS接收机,首先建立天线参考系,假设式(1)中的 PCO相对于天线参考系是固定不变的,则PCO的值可以通过参数估计得出。PCV的计算方法一般都采用一个相对于天线参考系在水平方向和垂直方向都连续的周期函数来模拟与卫星方位角和高度角相关的 PCV。文献[9]使用球谐函数来模拟PCV。

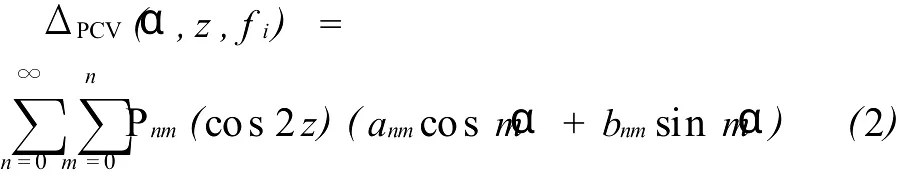
式中,Pnm(cos 2z)为勒让德函数;m、n、a、b分别为次数、阶数和待估参数。

该方法的优点是其具有较好的物理意义,但该方法所需要估计的系数较多,计算量很大,一般的计算机很难承受。一个比较简单并且容易实现的方法就是使用分段线性函数来描述与方位角和高度角有关的PCV[6,9]。其基本计算模型如下。

假设PCV模型由不同的网格点构成,每个格网均由4个待求PCV点组成,如图1所示,PCV在格网待求点A、B具有相同的高度角和不同的方位角,而A、C两点具有不同的高度角但具有相同的方位角。假设观测时刻的高度角和方位角位于AB CD的网格内,则 P点的 PCV值采用线性内插得到

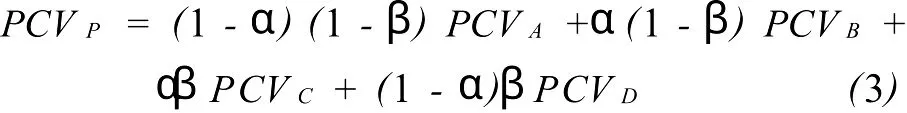
式中 ,α =(a-a1)/(a2-a1);β =(z-z1)/(z2-z1)。

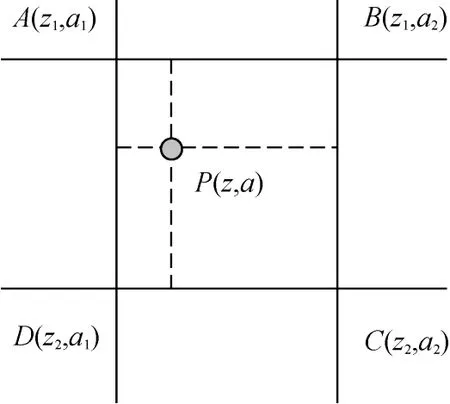
图1 PCV网格点线性插值示意图Fig.1 PCV grids linear interpolation

这两种方法所得到的PCV值差别不大,但后一种方法更能方便地植入应用软件中,本文将采取这种方法。

3 数据处理

3.1 GNSS精密定轨处理策略

GRACE卫星搭载有高质量的 GNSS星载接收机,使用 GPS、SLR系统和 K波段测距系统进行跟踪观测,并且所有这些观测值都能够免费获取,因此借助武汉大学自主研制的 PANDA软件平台,以 GRACE卫星作为研究载体来分析PCV对低轨卫星精密定轨的影响。

笔者采取三种数据处理方案来分析天线相位中心变化对 GNSS精密定轨的影响。不估计PCO和PCV而直接进行定轨(方案1);直接精密定轨且仅考虑PCO(方案2);先估计PCO值然后将其作为强约束再估计PCV(方案3)。分别对这三种方案精密定轨处理后,然后与精度较高的激光测距系统(SLR)和 KBR跟踪数据进行比较分析来验证PCV模型对精密定轨的精度影响大小。

3.2 观测模型和动力模型的建立

本文采用分段线性函数建立PCV模型。为了能够较为准确地估计PCV值,本文采用5°×5°网格点进行线性分段模拟,共有1 368个参数需要估计,因此必须保证足够数量的观测值并尽可能地覆盖整个天线零高度角以上的整个视场。首先采用2007年3月共31 d的数据采用最小二乘的方法获得PCO的估值,然后将 PCO作为已知值估计参数PCV。

由于低轨卫星仍未摆脱大气阻力和电离层的影响,所以无法对单个频率上的PCO和PCV进行估计,只能采用相位LC组合来消除无电离层的影响;大气阻力通过参数估计的办法加以消除;为了精确确定LEO卫星的姿态,使用 GRACE姿态数据;太阳光压模型所需的电磁参数和太阳辐射流等。与其他低轨卫星动力学环境类似,GRACE动力模型可参考低轨卫星CHAMP精密定轨处理策略[4]。其余部分参数设置如表1所示。

表1 数据处理参数设置Tab.1 Data processing parameter setting

4 定轨结果分析

4.1 观测值覆盖情况

在估计PCV时,按高度角和方位角分割的网格越多所估计的参数就越多,为了避免法方程奇异,观测值应尽量覆盖所建立的PCV模型的整个区域,亦即各个网格点上都应有观测数据。图2显示了 GRACE A星观测时间为24 h的观测值覆盖情况(高度截止角为0°)。

图2 GRACE A 24 h观测值覆盖情况(2007060)Fig.2 GRACE A 24 h observation distribution(2007060)

由图2可知,在连续观测24 h的观测值中,绝大部分观测值集中在高度角为10°以上,这部分观测值基本覆盖了10°以上的PCV模型的网格区域,但对于5°×5°网格点来说,仍有部分区域没有观测值而出现“空洞”需要通过多天的观测数据加以弥补。由图2,10°以下的观测值非常少,笔者对参与计算的连续观测31 d数据进行分析,发现各天的观测值分布很相似,10°以下的观测值都非常少,这样少的观测数据对于0～10°之间的PCV参数的估计十分不利,为避免法方程出现奇异,对所估计的PCV参数进行了较松弛的约束。

4.2 观测值残差分析

观测值残差包含模型化误差和未被模型化的误差。因此观测残差的均方差计算结果的内符合精度检验主要方法之一[4]。当 GNSS精密定轨采用的观测模型和力模型与实际情况十分吻合时,观测残差接近噪声水平[10]。根据式(1),对于所建立的PCV模型,有

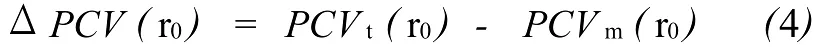
式中,PCVt、PCVm表示实际 PCV值和 PCV模型值。这两者的差值将直接反映在线性化后的观测残差中

未被模型化的ΔPCV(r0)值将会部分残留在事后处理的观测值残差中,该值随高度角和方位角变化关系在简化动力学定轨的观测值残差中尤为明显[11]。因此有学者直接从观测残差中拟合提取PCV值[5],该方法计算简单,非常容易编程实现,但实际上反映在残差中的误差并非只有未被模型化的PCV值,所以该方法得到的PCV值不一定与实际PCV值相符。本文按上述三种方案进行了精密定轨处理,根据图3所示,采用CODE分析中心的精密钟差和精密星历进行GRACE精密定轨,直接采用 GRACE观测文件给出的ENU值并进行改正后,将 GRACE卫星轨道和钟差等参数作为参数并不估计 PCO和PCV时,相位观测残差平均为8.5 mm,这说明模型化不太理想,可能原因是有比较大的误差项未考虑或者观测值文件中给出的ENU值与CODE分析中心的精密钟差和星历不一致。当把GRACE卫星的PCO作为未知数估计后的相位残差 RMS值约为 4.7 mm,减少了 45%;再将PCV作为参数估计后其残差进一步减小约0.5 mm。因此正如所期望的,以上三个方案进一步证实了式(5)分析的正确性。同时还说明PCO和PCV值以系统性误差的形式存在于观测值中,图中清晰看出方案1和方案2的残差RMS存在约为4 mm的系统误差。另一方面,相位残差均方差达到4 mm的水平也说明考虑相位误差校正后的观测模型和力模型与实际情况吻合得较好,未被模型化的误差进一步减小。

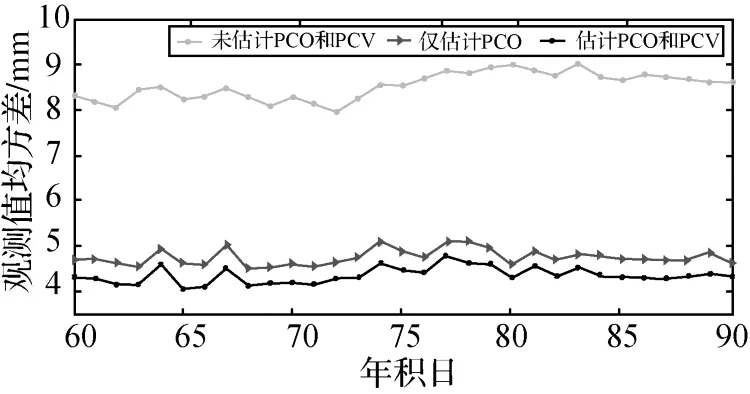
图3 观测值残差RMS统计Fig.3 Observation residual RMS statistics

4.3 精密定轨结果评价与分析

4.3.1 与JPL精密轨道比较

对精密定轨结果的评价除了观测残差分析外,另一个内符合精度方法是跟其他机构的定轨结果进行比较。JPL发布了官方的 GRACE精密定轨结果,其轨道精度在2～3 cm量级并经过了广泛的验证[10],因此本文的定轨结果与JPL进行了比较。

以 GRACE A星为例分析对象,GRACE B星也有类似结果。与J PL的精密轨道相比,当未估计PCO和PCV值时,径向误差和法向误差很大,分别达到32 mm和25 mm。这主要是因为未模型化的相位误差在 GPS-GRACE视线方向的影响较大,而切向方向较弱的几何约束使得很容易被较大的模型误差影响。法向RMS最小,仅为15 mm,似乎受模型化误差的影响不大,这也可以从另外两个方案的比较结果得到证实。估计相位误差PCO和PCV后,定轨精度得到明显提高,尤其是径向和切向,提高了5 mm～10 mm,这显然是估计PCO和PCV后相位误差被大大削弱的结果。是否估计PCV得到的定轨结果影响不大,估计PCV后定轨结果与JPL相比反而有所变差。可能的原因是JPL处理GRACE数据时没有PCV的影响,而使得其定轨结果仍包含PCV误差的影响或者在估计PCV时引入过多的参数而使得解不够稳定导致的。

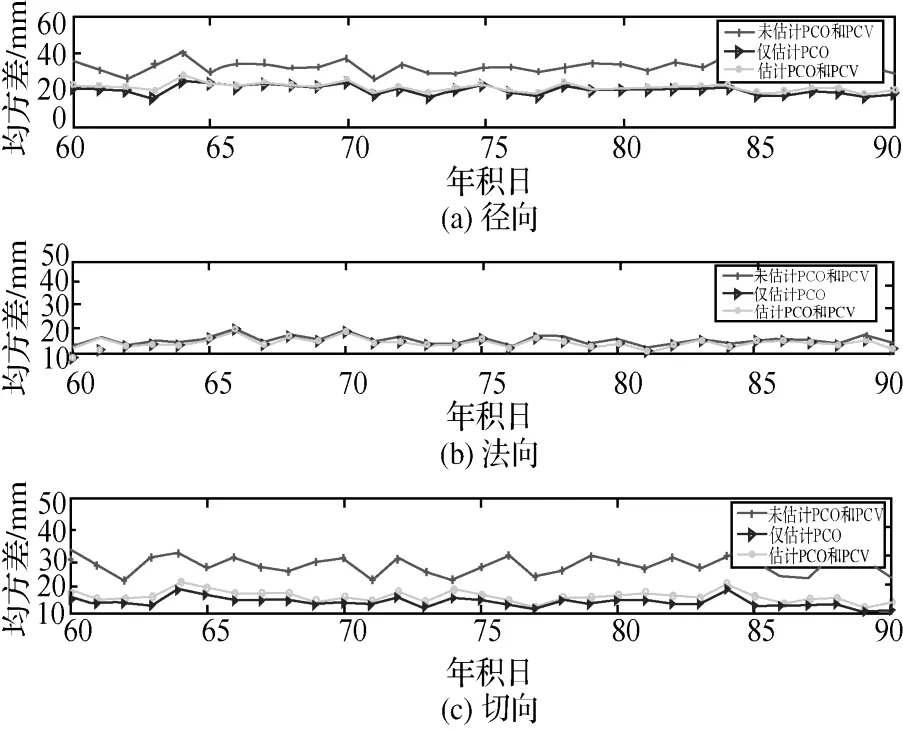
图4 定轨结果与J PL轨道比较Fig.4 Comparison between POD and J PL results

4.3.2 与 K波段测距比较

GRACE卫星配备了高精度的K波段测距系统(KBR),虽然该系统只能测得 GRACE双星的相对距离但其观测精度达到10-6量级,故 KBR是检验定轨精度的重要方法之一。如图5所示,三种定轨结果与KBR做差的标准差STD分别为2.95 mm、1.80 mm和1.46 mm。估计CPO后,轨道相对距离精度提高1.15 mm;考虑PCV估值后精度进一步提高0.4 mm。结果说明考虑PCO和PCV对GRACE基线的精度有所提高。

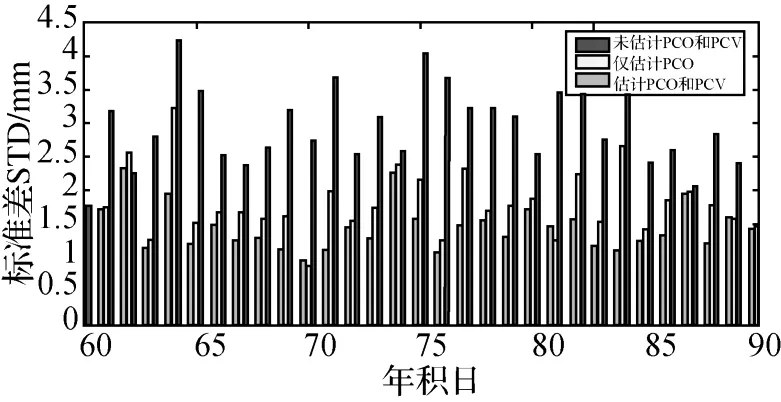
图5 KBR残差STD统计Fig.5 KBR residual STD statistics

4.3.3 与激光测距比较

GPS内符合精度并不能全面反映定轨结果的准确度,因此借助外部更加精密的测量手段来评价定轨精度显得更为客观。使用激光测距(SLR)数据来评价本文的定轨结果。SLR是独立于 GPS的精密测距系统,其测距精度很高,是目前卫星定轨主要的外部检核手段。

利用全球SLR站处理31 d的定轨数据得到的均方差值分布情况如图6。当估计 PCO和PCV时定轨精度明显高于不估计 PCO和 PCV(约为2.7 cm);而仅估计 PCO和估计 PCO、PCV两种方案的结果十分接近,分别为2.10 cm和2.0 cm。SLR残差结果说明前面分析的J PL和KBR的结果基本与实际情况相吻合。

图6 SLR残差RMS统计图Fig.6 SLR residual RMS statistics

5 结 论

本文首先阐述了估计天线相位中心的基本模型,然后利用31 d的 GRACE实测数据计算PCO和PCV,结果表明估计 PCO对 GRACE定轨结果有明显的改进。内符合精度方面,观测残差降低40%;与J PL公布的精密星历相比,估计 PCO对法向精度影响不大而对径向和切向有明显的改善,当估计PCO后三个方向的精度基本一致。外符合精度方面,高精度的 KBR数据残差结果表明估计PCO和PCV后GRACE双星基线结果有较为明显的改进,达到1.46 mm;最后通过激光测卫数据对定轨结果进行了比较,进一步验证了估计相位误差能够改进定轨结果。

[1] KUANG D,BAR-SEVER Y,BERTIGER W,et al.Precise Orbit Determinatibn for CHAMP Using GPS Data from Blackjack Receiver[EB/OL].[2011-01-03].Http:∥trsnew.jpl.nasa.gov/dspace/bitstream/2014/12198/1/01-0133.pdf.

[2] HAINES B,BERTIGER W,DESAI S,et al.Initial Orbit Determination Results for Jason-1:towards a 1-cm Orbit[C]∥Proceedings ofION GPS 2002.Oregon:[s.n.],2002.

[3] KANG Z,TAPLEY B,BETTADPUR S,et al.Precise Orbit Determination for the GRACE Mission Using Only GPS Data[J].Journal of Geodesy,2006,80(6):322-331.

[4] ZHAO Qile,LIU Jingnan,GE Maorong,et al.Precision Orbit Determination of CHAMP Satellite with cm-level Accuracy[J].Geomatics and Information Science of Wuhan University,2006,31(10):879-882.(赵齐乐 ,刘经南 ,葛茂荣,等.CHAMP卫星cm级精密定轨[J].武汉大学学报:信息科学版,2006,31(10):879-882.)

[5] MONTENBRUCK O,GARCIA-FERNANDEZ M,YOON Y,et al.Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J].GPS Solutions,2009,13(1):23-34.

[6] JÄGGI A,DACHR,MONTENBRUCK O,et al.Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J].Journal of Geodesy,2009,83(12):1145-1162.

[7] LI Zhenghang,HUANGJinsong.GPS Surveying and Data Processing[M].Wuhan:Wuhan University Press,2005.(李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.)

[8] CHENG Pengfei,CAI Yanhui,WEN hanjiang,et al.GNSS-Global Navigation Satellite Systems GPS,GLONASS,Galileo and More[M].Beijing:Surveying and Mapping Press,2007.(程鹏飞,蔡艳辉,文汉江,等.全球卫星导航系统GPS,GLONASS,Galileo及其他系统[M].北京:测绘出版社,2007.)

[9] ROTHACHER M,SCHAER S,MERVART L S,et al.Determination of Antenna Phase Center Variations Using GPS Data[C]∥Proceedings of theIGS Workshop.Potsdam:IGS,1995.

[10] ZHOU Xiaoqing,HU Zhigang,ZHAN G Xinyuan.Discussion on POD Accuracy Evaluation for Satellite-bone LEO Satellite[J].Geomatics and Information Science of Wuhan University,2010,35(11):1342-1345.(周小青,胡志刚,张新远.低轨卫星星载 GNSS精密定轨的精度检核方法[J].武汉大学学报:信息科学版,2010,35(11):1342-1345.)

[11] JÄGGI A,HUGENTOBLER U,BOCK H,et al.Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data[J].Advances in Space Research,2007,39(10):1612-1619.

(责任编辑:雷秀丽)

Research on Impact of GPS Phase Center Variation on Precise Orbit Determination of Low Earth Orbit Satellite

HU Zhigang1,2,ZHAO Qile2,GUO Jing1,2,LIU Jingnan2
1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Research Center of GNSS,Wuhan University,Wuhan 430079,China

All the L EO mission officials have published precision orbit determination results without phase center variation(PCV)information.In fact,PCV error is one of the main source of errors for precise orbit determination(POD).In this paper,the PCV error model is established and based on GRACE real data,the PCV is gained directly from estimatedparameters.Finally,some evaluations are conducted with K-band ranging data and satellite laser ranging data.

phase center variation;precise orbit determination;low earth orbit satellites;antennas;GPS

HU Zhigang(1982—),male,PhD candidate,majors in precise orbit determination for space-borne GNSS low earth orbiting satellites.

P228

:A

1001-1595(2011)S-0034-05

2011-01-10

修回日期:2011-03-22

胡志刚(1982—),男,博士生,主要研究方向是星载 GNSS低轨卫星精密定轨。

E-mail:zhigang.hu@whu.edu.cn