卫星导航中几何精度衰减因子最小值分析及应用
2011-11-04李建文李作虎斯顺杰
李建文,李作虎,周 巍,3,斯顺杰
1.信息工程大学测绘学院,河南郑州450052;2.武汉大学卫星导航定位技术研究中心,湖北武汉430079;3.63883部队,河南 洛阳 471003;4.78138部队,四川成都 610036
卫星导航中几何精度衰减因子最小值分析及应用
李建文1,2,李作虎1,周 巍1,3,斯顺杰4
1.信息工程大学测绘学院,河南郑州450052;2.武汉大学卫星导航定位技术研究中心,湖北武汉430079;3.63883部队,河南 洛阳 471003;4.78138部队,四川成都 610036
DOP是评估卫星导航定位性能的重要手段之一。在分析 GDOP的数学意义和测量意义的基础上,提出两种GDOP最小值的求解方法,并对最小值进行理论分析。结果表明,传统场合中认为DOP为“精度衰减”因子是有局限性的;随着卫星与用户几何关系的改变,包括 GDOP在内的所有DOP完全可以小于1,从而具有一定的精度增强作用。在此基础上,提出一种评价星座空间分布均匀程度的星座几何构型品质因数,并以GPS和Galileo星座为例进行试验,结果表明该因数可以较好地评价星座的空间分布均匀程度。基于 GPS星座在近地空间内导航精度性能的试验结果很好地证明了DOP具有精度增强的属性。
卫星导航;精度;精度因子;星座;性能评估
1 引 言
精度因子(dilution of precision,DOP)作为评估卫星导航定位性能的重要手段之一,不仅具有测量意义,还具有明确的数学意义。在测量上,DOP反映了由于观测卫星与接收机空间几何布局的影响造成的伪距误差与用户定位授时误差间的比例系数,是评估用户定位授时精度的重要内容;根据用户在测量中关注的性能指标不同,DOP可细分为 GDOP、PDOP、HDOP、VDOP 和TDOP,具体的定义可以参考早期的 GPS经典文献[1]。在数学上,DOP作为基于最小二乘平差解的权逆阵对角线的重要组成部分,同时也是未知参数协方差对角线元素与伪距等效方差的比值,反映了观测信息对于解算的未知参数的贡献程度[2]。但无论是在测量上还是在数学上,DOP都反映了导航解的质量,与导航解具有同样重要的地位。然而,由于历史原因,DOP产生于 GPS理论中 ,其字面意思为“Dilution Of Precision”,所以大多传统场合都称其为精度衰减因子;因为其确实在一般场合中作为一个放大因子来体现星地空间几何对于由于测距误差而导致对定位授时误差的影响,故文献[1]指出 GDOP的典型值为1~100。而事实上,以 GDOP为例,在数学上,其最小值要小于1,GDOP将不再仅仅是一个精度衰减因子,而是一个精度增强因子,而这个结论在测量上也是存在的,而且具有积极的意义。本文将推导这个结论,并给出其在某些方面的应用价值。
2 GDOP最小值的求解
卫星导航定位中,通常选择4颗或4颗以上的可视卫星进行导航定位解算,其用户位置和时间偏差参数误差的协方差矩阵为 G=(HTH)-1,其中 H是导航定位解算方程的系数矩阵,通常称为观测矩阵,如下式

式中,axi,ayi,azi(i=1,2,…,n)分别表示用户与可视卫星之间方向矢量的余弦;n为可视卫星的数目。因此,具有以下数学关系
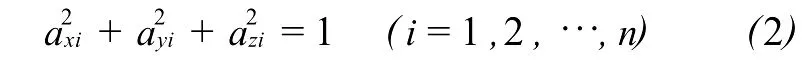
由于 GDO P=(tr(HTH)-1)1/2,需要计算HTH如下

根据矩阵迹的定义可得:tr(HTH)=2n。设λi(i=1,2,3,4)是 HTH的特征值,则有

此时,GDOP可表示为
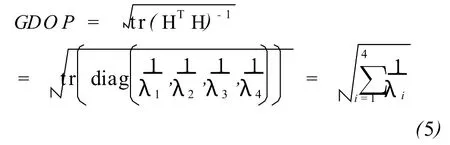
此时,GDOP最小值的求解已经转化为矩阵HTH特征值值域的估计问题。如果不考虑 HTH特征值的值域差异,即存在四个特征值相等的情况,则可以利用正数的几何平均值总是小于它们的算数平均值来获得 GDOP的最小值。但事实上从式(3)可见,HTH的第4行、第4列的对角元素总是n,而其他行与列的对角线元素具有相似性,下面用矩阵论中的盖尔斯高林(Gerschgorin)圆盘定理说明前三个特征值的值域相同[3]。
根据盖尔斯高林圆盘定理,对于复数域内的矩阵 HTH,对应的四个 Z平面上的圆盘分别为
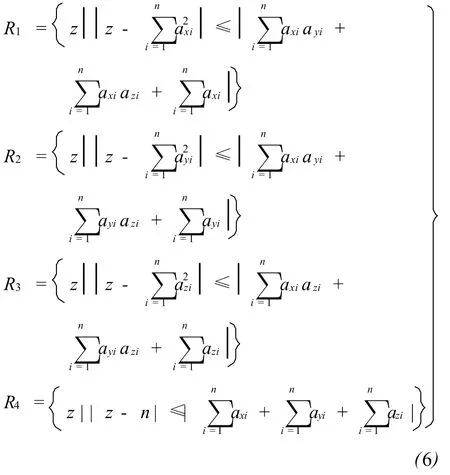
该定理指出矩阵的特征值与其对应的圆盘具有一定关系,而从式(6)中可知,前三式具有轮换对称性,而第四式却明显不同于前三式。据此可以认为 HTH的前三个特征值具有相同的值域,而第四个特征值则具有不同于前三个特征值的值域。
事实上,可以采用反证法证明λ4≥n,具体可见文献[4],在此不再赘述。
至此,即可采用不等式求解(5)式的最小值
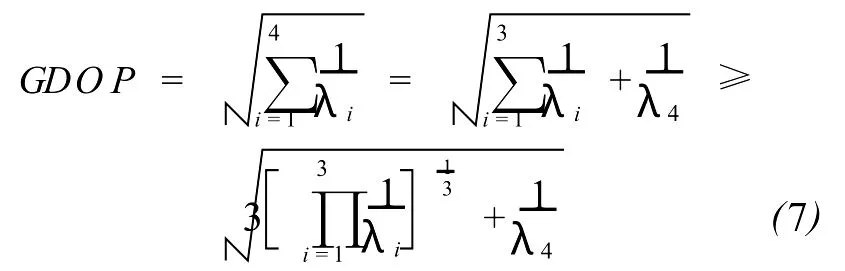
其中,当且仅当λi(i=1,2,3)相等时等号成立。考虑到式(4),可以将 GDOP用λ4表示;又由于λ4≥n,即得当λ4=n时 GDOP获得最小值
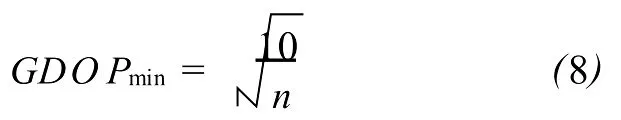
下面从测量的角度来证明这个结论。
在用户坐标已知的情况下,只有一个未知量,即接收机钟差,此时观测方程为 H4=[1…1]T,则 HT4H4=n,且 GDOP退化为在特殊条件下的TDOP,即可得

同理,如果不考虑钟差或认为钟差已知,则可得tr(HT3H3)=n,其中 H3表示去掉钟差系数的观测矩阵,故 HT3H3为矩阵式(3)HTH的前3行前3列组成的对称方阵。此时,GDOP则退化为PDOP,即

上式在λi(i=1,2,3)相等时等号成立。再结合式(4)以及式(9)成立的关系可得
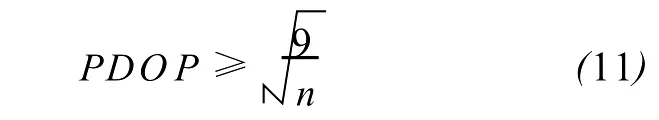
综合式(9)和式(11)可得到

文献[4]还给出了 GDOP最小时须满足如下条件
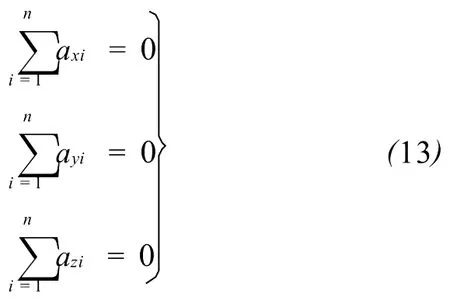
可见当用户处于多颗可视卫星形成的均匀多面体的中心时,GDOP最小,定位精度最高。上式亦表明此时每个轨道面上的卫星都是均匀分布的。另外,式(8)亦表明 GDOP最小值也是可视卫星数目的函数,有效可视卫星数越大,则 GDOP最小值越小。
3 构建星座几何构型品质因数
根据式(13),依据 GDOP最小时需要满足的条件可构建用于描述星座几何构型的品质因数(constellation geometry factor,CGF),用来描述星座空间布局的均匀程度。笔者分别提出如下两个因子:
瞬时CGF为

平均CGF为
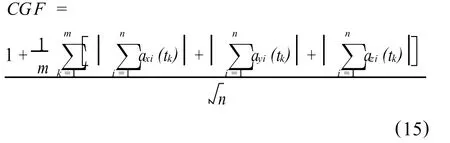
其中,n为可视卫星数目;m为星座运行周期内等间隔采样的个数。在计算 axi、ayi、azi(i=1,2,…,n)时假定用户位于地球质心。
分析式(14)瞬时CGF,可得出以下结论:
(1)用户处于多颗可视卫星形成的均匀多面体的中心时,CGF=1/n,仅仅与可视卫星数目有关。该结论表明,此时星座可视卫星越多,则CGF越小,星座几何构型品质越高。
(2)用户处于多颗可视卫星形成的不均匀的多面体的中心时,CGF不仅与星座的可视卫星数目有关,还与星座卫星布局的均匀程度有关。CGF越小,则星座卫星布局越均匀,其构型品质越高。
要分析星座的几何构型品质,需要采用式(15)平均CGF模型,并在星座的运行周期内进行统计分析和量化比较,从而得出对于星座几何构型的综合评价。下面分别以 GPS与 Galileo星座为例计算平均CGF进行比较分析。其中 GPS的星座数据来自实测历书,其许多卫星的轨位已与标称星座给出的轨位相差很大[5];Galileo星座是根据发布的标称星座仿真得到。
表1数据反映了 GPS和 Galileo星座的几何构型品质因数的比较。虽然 GPS星座在卫星数目上要略微优于 Galileo,但 Galileo星座在空间均匀度上要明显由于 GPS。其原因不仅在于GPS设计星座不对称,还在于GPS星座经过长期运行,部分卫星轨位已经发生明显改变,从而在一定程度上破坏了标称星座原有的均匀度。

表1 GPS与 G alieo星座的平均CGF比较Tab.1 Mean CGF comparison between GPS and G alileo constellations
4 基于空间布局结构的导航性能增强
目前 GNSS的服务空域(service volume)主要指全球地面或地表的空间区域,因而对于GNSS用户而言,由于受到最低卫星截止角的限制,其可视卫星基本分布在用户所在平面的一侧,即所有可视卫星的高度角都为正。根据式(13)分析可知,这种很不均匀的卫星空间布局将会导致较大的GDOP产生。
目前随着卫星导航技术的提高和空间探测活动的迅猛发展,未来 GNSS的服务空域将会得到极大的扩展,从地面几十千米到离地面几千千米的近地空间将成为 GNSS的重要应用领域[6-7]。在这种应用背景下,用户与可视卫星的几何空间布局结构将得到极大的改善:可视卫星不再仅分布于用户所在任意平面的一侧,负高度角的可视卫星亦可得到有效利用,从而提高用户导航定位授时的精度。不仅如此,这种导航定位精度性能的增强将会使得传统的 GDOP性质发生本质改变:从“精度衰减”因子到“精度增强”因子。图1为中纬度单点(E113°,N34°)在不同高度条件下同一时刻 GPS各种DOP值与可视卫星数目之间的变化关系。需要强调的是随着用户离地面高度的增加,部分高度角为负的卫星亦可视,可采用双天线模型分别采集高度角为正的可视卫星和高度角为负的可视卫星的数据[5]。其中高度角为负的卫星可视条件的判断需要依据用户高度、地球半径以及临界条件下卫星与用户连线与地球相切的几何条件来完成,相关讨论不是本文研究的重点,可参考文献[8—10]。地面10 km以下采用5°卫星截止角,10 km以上采用负截止角。
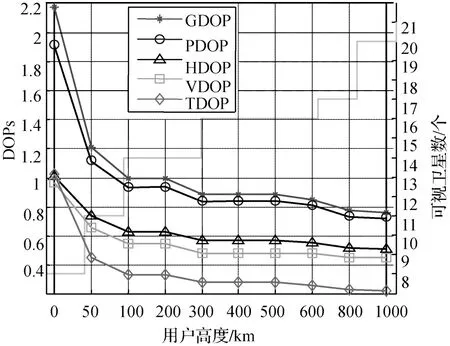
图1 近地空间不同高度条件下的DOP值比较Fig.1 Comparison of DOPs at different heights in near space
正如图1所示,随着用户高度的增加,星地空间几何关系发生了明显变化,各类DOP都有明显减小,GDOP在用户高度大于100 km时就开始小于1,成为名副其实的“精度增强”因子。目前,这种基于空间布局结构的 GNSS性能增强其实已经得到了实际应用,这就是利用伪卫星对高空用户的性能增强。这种方法可以实现区域导航性能的改善,不仅包括精度,还将对完好性、连续性以及可用性加以增强,从而满足高空用户导航定位授时的需求。
5 结 论
在分析卫星导航中DOP的数学意义和测量意义的基础上,分别从数学角度和测量角度给出了求解GDOP最小值的方法。结论表明,GDOP最小值不仅与星地几何空间有关系,还与参与计算的卫星数目有函数关系。在此基础上构建了星座几何构型品质因数,并用 GPS和 Galileo星座进行了试验,结果表明该因数可以反映星座空间几何分布的均匀程度。最后分析了基于空间布局结构的导航性能增强方法,并用试验证明了DOP具有“精度增强”的属性。基于该结论,笔者认为,DOP应该称为“精度因子”更为恰当,而不应该冠以“衰减”来限定。
[1] PARKINSON B W,SPIL KER J J,AXELRAD P,et al.Global Positioning System:Theory and Applications(Volume I)[M].[S.l.]:American Institute of Aeronautics and Astronautics Inc,1994.
[2] CONG Li,ABIDAT A I,TAN Zhanzhong.Analysis and Simulation of the GDOP of Satellite Navigation[J].Acta Electronic Sinica,2206,34(12):2204-2209.(丛丽,ABIDAT A I,谈展中.卫星导航几何因子的分析与仿真[J].电子学报,2206,34(12):2204-2209.)
[3] BU Changjiang,LUO Yuesheng.Matrix Theory[M].Harbin:Harbin Engineer University Press,2003:164-174.(卜长江,罗跃生.矩阵论[M].哈尔滨:哈尔滨工程大学出版社,2003:164-174.)
[4] SHENG Hu,YANGJingshu,ZENG Fangling.The Minimum Value of GDOP in Pseudo-range Positioning[J].Fire Control&Command Control,2009,34(5):22-24.(盛琥,杨景曙,曾芳玲.伪距定位中的GDOP最小值[J].火力与指挥控制,2009,34(5),22-24.)
[5] DEPARTMENT of DEFENSE USA.Global Positioning System Standard Positioning Service Performance Standard[M].4th ed.Washington DC:[s.n.],2008.
[6] YAN Lijin.Near Space and Electronic Information Warfare[J].Electronic Warfare,2007(2):1-3.(阎立金.近地空间与电子信息战[J].电子对抗,2007(2):1-3.)
[7] J IAN G Pucheng,WU Tanran,ZHAN G Yuhan.The Developing Conditions and Tendency of Near Space Airship[J].Space Electronic Technology,2008,5(3):5-10.(蒋谱成,武坦然,张宇涵.近地空间飞艇发展现状与趋势[J].空间电子技术,2008,5(3):5-10.)
[8] ZHANG Zhi,YUAN Jianping,CHEN Shilu.Applications of GPS in Space[J].Journal of Astronautics,1996,17(3):68-71.(张志,袁建平,陈士橹.GPS的空间应用[J].宇航学报,1996,17(3):68-72.)
[9] LIU Huijie,ZHANG Naitong.Research of Space Coverage Property for GPS Constellation[J].High-tech Communication,1999(12):1-5.(刘会杰,张乃通.GPS星座的空间覆盖特性研究[J].高技术通讯,1999(12):1-5.)
[10] MAO Kecheng,SUN Fuping,LI Hongtao,et al.Modeling and Simulation of GPS Signal Blockage Based on Space Resection[J].Hydrographic Surveying and Charting,2007,27(4):36-40.(毛克诚,孙付平,李洪涛,等.基于空间交会GPS信号遮挡模型的建模与仿真[J].海洋测绘,2007,27(4):36-40.)
(责任编辑:马保卫)
Study on the Minimum of GDOP in Satellite Navigation and Its Applications
LI Jianwen,LI Zuohu,ZHOU Wei,SI Shunjie
1.Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052 China;2.Research Center of GNSS,Wuhan University,Wuhan 430079 China;3.63883 Troops,Luoyang 471003 China;4.78138 Troops,Chengdu 610036 China
The DOP is one of the ways to assessment the performance of satellite navigation and positioning.Based on the mathematical and surveying meanings of GDOP,two methods to get the minimum of GDOP were given,and the study on the minimum was made theoretically.The conclusion was drawn that,the traditional idea that DOP is just a factor to decrease the navigation&positioning precision was limited,since all DOPs including GDOP would certainly be less than one and improve the precision as a result with the change of geometrical relationship between satellites and users.On the basis of the above conclusions,CGF(Constellation Geometry Factor),which could be used to assessment the spatial geometrical layout characteristics of constellation,was given.The Test with GPS and Galileo constellations had shown that CGF could give an effective evaluation the spatial geometrical layout characteristics of constellation.The Test on the navigation precision performance in near-earth space with GPS constellation proved that DOP has the attribute to improve precision.
satellite navigation;precision;DOP;constellation;performance evaluation
LI Jianwen(1971—),male,associate professor,majors in satellite navigation system test and navigation&positioning applications.
P228
:A
中国卫星导航学会青年优秀论文获奖者资助课题基金(CSNC2010-QY-012);信息工程大学博士研究生学位论文创新基金(YJ201004);卫星导航与定位教育部重点实验室(B类)开放课题基金(GRC-2009005)
1001-1595(2011)S-0085-04
2011-1-25
修回日期:2011-3-25
李建文(1971—),男,副教授,主要研究卫星导航系统测试及导航定位应用。
E-mail:zzljw@126.com
