模数转换器对导航信号的影响分析及最优量化参数选择方法设计

王 尧,崔晓伟,陆明泉

清华大学电子工程系,北京100084

模数转换器对导航信号的影响分析及最优量化参数选择方法设计

王 尧,崔晓伟,陆明泉

清华大学电子工程系,北京100084

结合导航信号的具体物理模型,从信息量和信噪比两个角度入手,对ADC前后导航信号所含有效信息量及信噪比变化规律进行推导计算。从理论上证明2～3 bit量化已能满足一般接收机正常工作的需要,在此基础上归纳不同的量化门限选择对信号信噪比的不同影响,发现在特定的干扰下,合理地选取量化门限反而会增加信号的信噪比这一反常规现象。最后提出一种合理选取量化门限的方法,以获得最优的信噪比增益,并进行了试验仿真的验证,对接收机前端设计具有一定的启发意义。

GNSS接收机;A/D量化;门限;信噪比

1 引 言

数字信号处理技术已广泛应用于电子相关领域。在导航用户终端,主要的数据处理模块也大都采用数字信号的处理方式。A/D量化作为模拟信号转向数字信号的桥梁,其不可避免地会引入一定的量化误差。提高量化精度可以更准确地反映真实信号,获得更理想的处理结果,然而这也会增加处理的计算和存储复杂度。在特殊工作需求(如抗干扰或高灵敏度接收机)中,往往需要较高的量化精度,采用12 bit或更高比特的量化。而在一般的民用接收机中,2～3 bit量化已能较好地满足处理所需。此外,相同的精度下,不同的量化参数带来的损耗影响也不尽相同,因此合理的选择量化方式是接收机前端的要点之一。

针对纯高斯白噪声和单个点频正弦波(CW)干扰两种信道模式,考虑2 bit A/D量化。从观察量化前后信号所含有效信息量及经典信噪比的变化入手,分析了不同参数下量化带来的不同影响。得出仅有高斯白噪声时,选择最优量化门限,2 bit A/D量化仅损失11%的有用信息,经典信噪比损失0.54 dB左右。而当信号中混入单个正弦波干扰信号时,选择特定的量化门限反而会增加信号的经典信噪比,带来一定的处理增益。文中提出了一套合理选取量化门限的方法,以获得最少的信息丢失。

2 A/D量化

2.1 量化方式

GNSS接收机中常采用中升型的量化方式,正负对称。以2 bit量化为例,共4个量化电平(-R,-1,1,R),若选取量化门限为0和±Δ,以Y和W分别以表示量化前后信号,则量化规则为

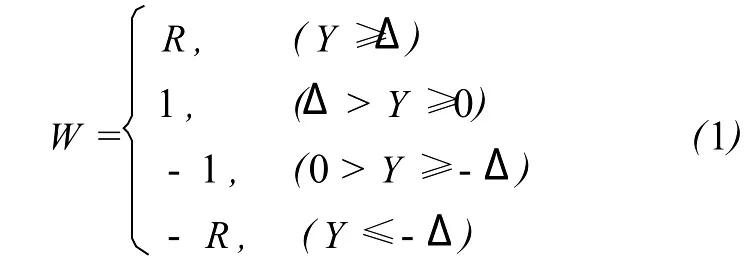
量化特性曲线如图1所示,均匀量化中 R=3。不同的量化门限和量化电平下,数据的量化结果和特性也不同。

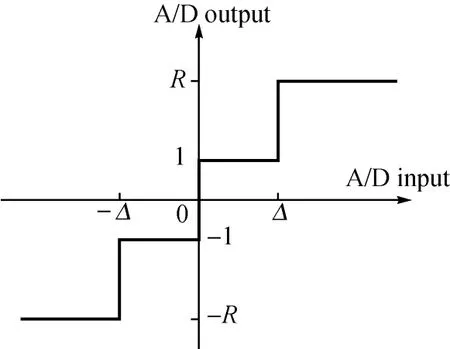
图1 2 bit A/D量化特性Fig.1 Characteristic of 2 bit ADC

2.2 相关理论参数及计算方法

以Y=X+Z+I表示输入信号,其中 X=1或-1为导航比特信号;Z为零均值高斯白噪声;I为特定的潜在干扰(如CW干扰)。在给定干扰类型以及输入信噪比 S N Rin、信干比SIRin后,即可精确地得到以上各随机变量的概率密度函数,根据量化准则,W的分布函数 P(W=w)也可以确定。

更进一步,可推出随机变量 Y、W 与 X、Z、I间的条件转移密度函数,然后求得条件熵H(X|Y)及 H(X|W),则 Y、W 与 X间的互信息为

互信息反映了量化前后混合信号中所包含的导航比特信息量,即有效信息量。通过一组变化参数下的计算结果对比,得到不同量化参数对有效信息量变化的影响,可为量化参数的选择提供有力的理论支持。

同时,通过计算 X=1时,W取值的期望v以及方差σ,即可以近似得到量化后信号的经典信噪比,这和 N点序列在统计意义上得到的信噪比结果是等价的。

3 量化参数影响及最优门限选取规律

这里仅考虑均匀量化,则有关参数主要为量化门限Δ。本节分析计算了三种噪声干扰下,不同门限参数对有效信息量和信噪比变化的影响。

3.1 仅有高斯白噪声时

接收信号Y=X+Z,其中 Z为高斯白噪声N(0,δ2),则其概率密度函数为

由全概率密度公式得

结合量化规则有

同理可求出 P(W=1)、P(W=-1)、P(W=-R),这样就得到了所有相关随机变量的概率密度函数。

为了得到量化前后信号与导航比特信号间的互信息 I(X;Y)和 I(X;W),需要求出 H(X|Y)和H(X|W),而

同理

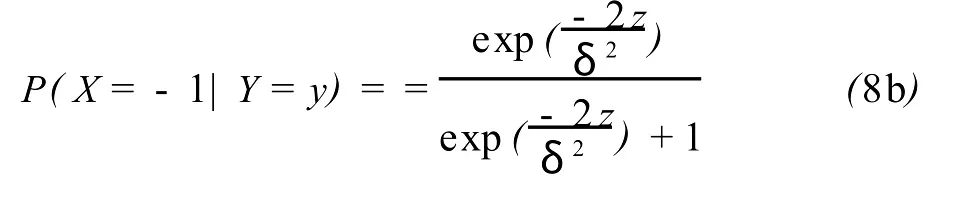
综合式(6)～式(8)可得 I(X;Y),同种计算方法可得I(X;W)。量化后信号信噪比同样可由概率密度函数推导出

令其输入信噪比 S N R=-25 dB,量化前后信号有效信息量和信号信噪比变化曲线如图2所示,横轴表示量化门限Δ与噪声标准差δ的倍数比值。

图2 高斯噪声下不同量化门限对应的有效信息量(a)及信噪比(b)的变化曲线Fig.2 The influence of ADC due to different quantification threshold(Gaussian noise)

观察图2(a),整体来说,量化后信号包含的有效信息量较量化前均有所降低,和信息论的“数据处理定律”一致。但门限Δ取约1倍噪声标准差δ时,有效信息量损耗有极小值,约占量化前原始信号所含有效信息量的11%,损失并不严重。而对比图2(b),量化以后信号的信噪比变化趋势和图2(a)中有效信息量变化曲线基本一致,这与“二者是对有用信息的不同刻画方式”这一本质也是相符合的。在信噪比曲线峰值处,量化具有最小的信噪比损失(约0.54 dB)。当采用更多bit的A/D量化时,该损耗会逐渐降低,计算可得,1 bit A/D量化信噪比约损耗-1.97 dB;3 bit A/D量化约损耗-0.17 dB;4 bit A/D量化约损耗-0.06 dB,当更加精确时,损耗趋近于0。

合理的选择量化门限,2 bit A/D量化的损耗已在普通的民用接收机处理容限之内,且消耗较少的运算和储存资源。

3.2 仅有单个正弦干扰时

当接收的信号仅受单个正弦波信号干扰时,Y=X+I,I=Acos(ωt+φ)为正弦波,其中 A 为幅度,ω、φ为频率与初始相位。

图3为标准正弦三角函数的值域概率密度,由此可得 I的概念分布函数如下

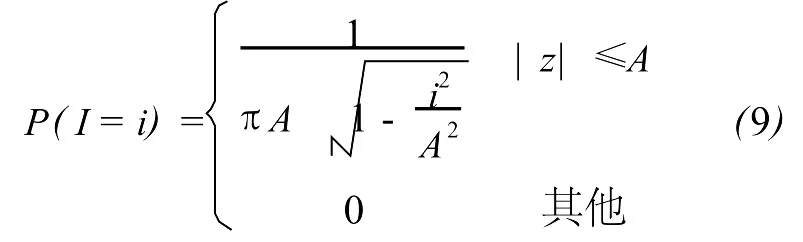
有效信息量与信噪比的计算方法与3.1中算法相同,只是此时概率密度函数会更为复杂,需要引入积分运算。限于篇幅这里略去详细推导过程。

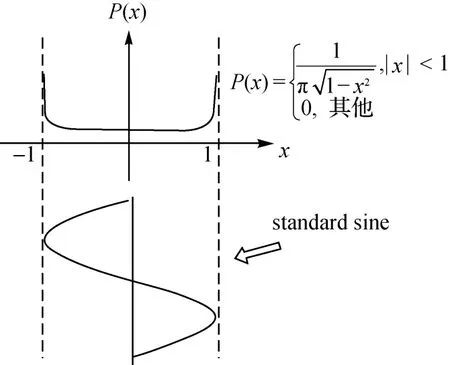
图3 标准正弦波的概率密度函数Fig.3 PDF of standard sine signal

取输入信干比S IR=-25 dB,量化前后信号有效信息量和信号信噪比变化曲线如图4所示,横轴表示量化门限Δ与正弦干扰幅值A的倍数比值。

观察图4(a),由于正弦干扰的特性,2 bit量化后有效信息量损失十分严重。然而,当量化门限取1倍正弦幅值A左右时,量化后有效信息量得到了最大的保留,损失仅 16%左右。对比图4(b),在Δ=A附近,所计算的信噪比不仅没有降低,反而有所增加。这和常情有一定的矛盾。原因可能因为经典的信噪比评价方法 S N R=(期望/方差)对于非线性处理后的量化结果而言,意义并不严格精确。然而,该参考量的变化趋势也为量化门限的选择方案制定提供了一定的依据。中曲线变化趋势和图4基本一致。当量化门限Δ取1倍正弦幅值A左右时,量化后信号保留了最多的有效信息量,经典意义上的信噪比也具有一定的提升。

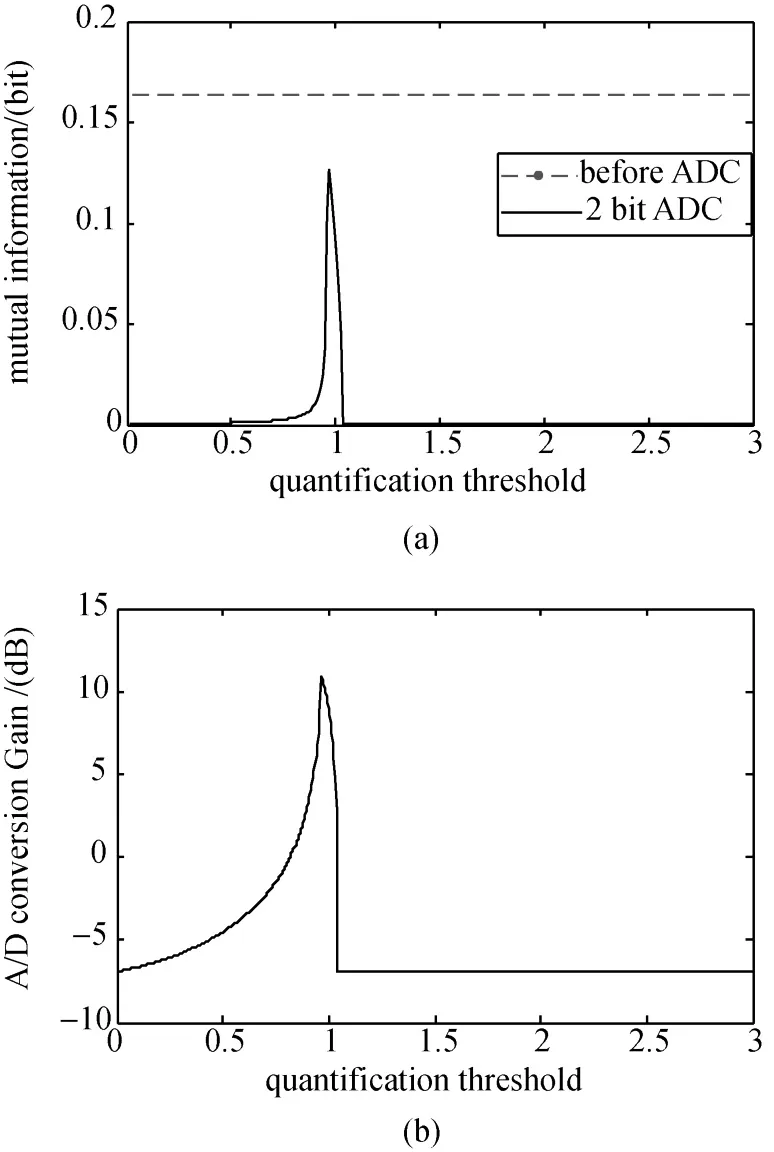
图4 正弦波干扰下不同量化门限对应的有效信息量(a)及信噪比(b)的变化曲线Fig.4 The influence of ADC due to different quantification threshold(CW interference)

3.3 高斯白噪声和单个正弦干扰

综合考虑高斯白噪声和单个正弦干扰的影响,此时Y=X+N+I,当正弦干扰占主要地位时,取输入信噪比为-25 dB,信干比为-40 dB,量化前后信号有效信息量和信号信噪比变化曲线如图5所示,横轴表示量化门限Δ与正弦干扰幅值A的倍数比值。观察图5,由于信号中噪声和干扰较强,信号中所含有的导航比特信息量量级(10-4)较小,即导航信号具有较强的不确定性,为了获得导航比特信号,需要更为复杂的后续处理流程。然而单从量化这一环节的影响来看,由于CW干扰比高斯白噪声要强很多,在信号中占主要地位,故图5

图5 高斯和正弦波共同干扰下不同量化门限对应的有效信息量(a)及信噪比(b)的变化曲线Fig.5 The influence of ADC due to different quantification threshold(Gaussian noise and CW interference)

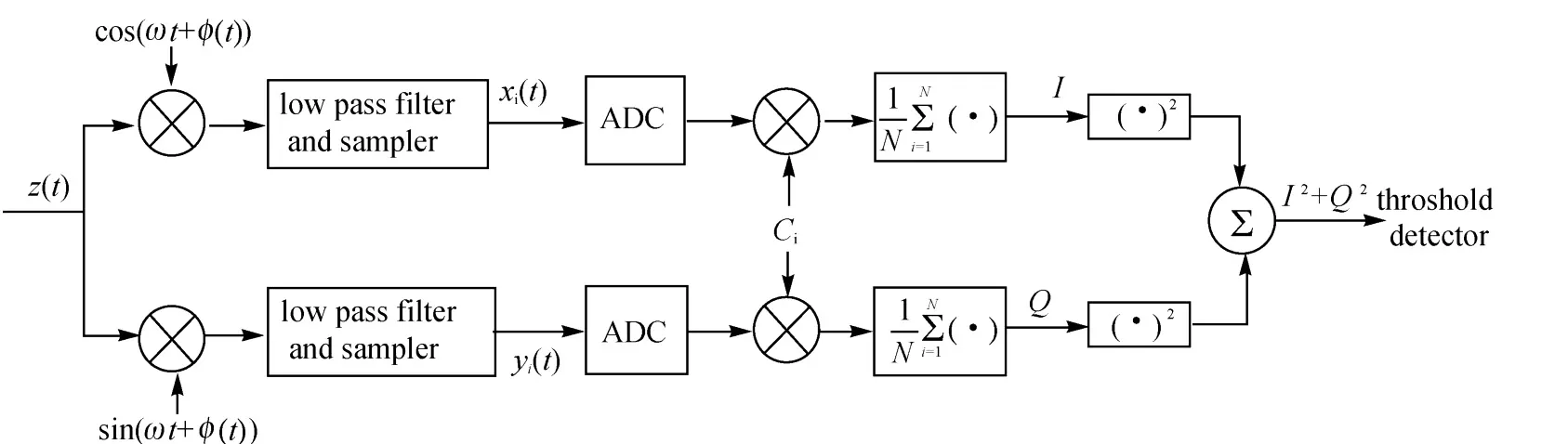
图6 接收机相关检测环路示意图Fig.6 The quadrature detection loop of the receiver

4 仿真试验

在MATLAB平台下,采用简化的 GPS C/A码接收机进行仿真试验,系统处理框图如图6所示[4],模拟信号经过载波剥离和低通滤波后得到两路正交信号,经过采样和AD量化后与本地码进行相关,然后对结果平方求和,这样就得到了捕获后的相关信噪比[2]

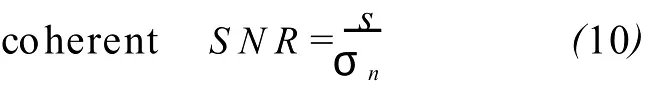
式中,s为有效相关峰值;σn为相关波形标准差如图7所示。相关信噪比反应了捕获性能的好坏,是判断是否达到后续跟踪处理条件的一个重要指标。

本节通过一组对照试验,观察不同门限参数的2 bit A/D量化对捕获性能的影响。

图7 捕获相关曲线示意图Fig.7 Representation of the correlation

4.1 高斯白噪声干扰

取采样率5 MHz,S N R=-13 dB,判决门限Δ取一组等间隔值,相关信噪比的结果如图8所示,横轴表示量化门限Δ与噪声标准差δ的倍数比值。

当Δ取1倍左右噪声标准差时,相关信噪比有峰值,此时较无量化精确值处理结果损耗最小,与理论计算结果一致。

图8 纯高斯白噪声下相关信噪比曲线Fig.8 Coherent SNR(Gaussian noise)

4.2 高斯白噪声和单个CW干扰

取采样率5 MHz,S N R=-20 dB,S IR=-37 dB,一组对比试验结果如图9所示。横轴表示量化门限Δ与正弦干扰幅值A的倍数比值。

由于高斯干扰的存在,相关信噪比较小,仅12 dB,与3.3节中理论计算结果一致,2 bit量化时,合理的选择量化门限,相关信噪比反而有所提高。其中峰值点对应的具体相关波形如图10所示,可以看出量化后波形变得稍微平缓一些,波动标准差降低,使得相关峰更为突出。

图9 高斯和正弦波共同干扰下相关信噪比曲线Fig.9 Coherent SNR(Gaussian noise and CW interference)

图10 峰值点对应的相关曲线——量化前(a)/后(b)Fig.10 Without ADC(a)/2 bit ADC(b)

5 结 论

本文系统地分析了几种常见类型的信号在2 bit A/D量化时,不同的量化门限对信号中所含有效信息量及其经典信噪比的影响。当仅存在高斯白噪声干扰时,取量化电平Δ为1倍噪声标准差δ左右可以获得最小的有用信息损失(约11%),信噪比损失约0.54 dB左右。此时基本满足普通民用所需,且所耗计算和存储资源较少。而当信号中混入较强的CW点频干扰时,取量化电平Δ为1倍正弦幅度A左右时,可以最小化有用信息丢失,且获取一定的经典信噪比增益。不同的信道可以采用相应的最优量化方法来获得更好的处理效果。

[1] ZHU Xuelong.Fundamentals of Applied Information Theory[M].Beijing:Tsinghua University Press,2001:27-31.(朱雪龙,应用信息论基础[M].北京:清华大学出版社,2001:27-31.)

[2] VAN DIGGELEN F.A-GPS:Assisted GPS,GNSS,and SBAS[M].Artech House,2009:171-175.

[3] AMOROSO F.Adaptive A/D Converter to Suppress CW Interference in Spread-spectrum Communications[J].IEEE Trans Commun,1983,31(10):1117-1123.

[4] ELLIOTT D K,CHRISTOPHER JH.Understanding GPS Principles and Application,Second Edition[M].London:Artech House,2007.

[5] LOHAN E S,SKOURNETOU D,Level Crossing Rate Estimation(LCRE):A New Technique for Finding GNSS Carrier to Noise Ratios[J].Inside GNSS,2010(9):36-42.

(责任编辑:张燕燕)

Analysis of ADC’s Effects on Navigation Signals and Optimal Parameter Selecting Method

WANG Yao,CUI Xiaowei,LU Mingquan
Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

A precise deducing about the changes of effective information of the navigation signal and signal-to-noise ratio is given,theoretically confirming that an ADC in 2 or 3 bits would meet most of the requirements in general receivers.Furthermore,the different influences,determined by the chosen AD threshold,are elaborated too.One result shows that in some very kind of interference,the signal-to-noise ratio increased after the ADC,which is profitable for the ensuing processes thought not agreeing with the common sense.Finally a solution of how to choose the AD threshold in the GNSS receiver so as to get a most gain(a least loss)is demonstrated,which has been proved by the simulation in Matlab project.

analog-to-digital converter;threshold;signal-to-noise ratio

WANG Yao(1988—),male,postgraduate,majors in signal processing ofGNSS and modeling of GNSS signal channel.

P245

:A

1001-1595(2011)S-0100-05

2011-01-28

修回日期:2011-03-24

王尧(1988—),男,硕士生,研究方向为GNSS信号处理及 GNSS信道建模。

E-mail:Yao_wang05@mails.tsinghua.edu.cn