结合实际谈数学教学中如何培养学生的观察能力

辽宁 李海波

结合实际谈数学教学中如何培养学生的观察能力

辽宁 李海波

数学观察能力是指在学习、生活中积极主动地获取数学信息,联系数学知识,构造数学模型,进而认识数学问题并解决数学问题的重要能力。本文从激活学生的观察兴趣，培养学生的观察能力；增强观察的目的性，提高学生的观察能力；边观察边思考，提高解决实际问题的能力几个方面对培养学生的观察能力进行了阐述。

数学；观察；兴趣；观察能力

教育的目的在于知识的传授和能力的培养。其中能力的培养对提高教学质量，提高受教育者的素质是非常重要的。对教师而言，他的工作不只是简单地传授知识，而应该是教会学生获取知识的同时，获得比知识更重要的观察、分析、概括、解决问题的实际能力。

数学教学，实质上是思维活动的教学，其教学过程是在教师的主导作用之下，使学生通过认识——实践——再认识——再实践这个过程掌握知识，获得分析问题、解决问题的能力。在这个过程中作为学习主体的学生，它不是知识的消极接受者，教师也不可能机械地把知识灌输到学生头脑中去，要想把人类积累的认识成果转变为学生的知识财富，进而转化为学生的智力才能，必须通过学生自己的积极思考和参与，充分调动学生学习的主动性，才能取得较好的教学效果。针对学生在学习中不善于观察、分析、概括的情况，教学中我着重在以下几个方面进行了尝试，并取得了较好的效果。

一、激活学生的观察兴趣，培养学生的观察能力

心理学认为：观察是一种有目的、有计划、主动并有思维参与的知觉过程；它是一种比随意注意更为自觉的积极的感知过程。数学观察能力是指人们有目的、有计划、有选择的、较持久的数学感知能力,是人们在学习生活中积极主动地获取数学信息,联系数学知识,构造数学模型,进而认识数学问题并解决数学问题的重要能力。培养观察能力是全面提高学生素质的重要环节。

培养学生的观察能力，首先要使学生对所观察的对象产生兴趣，激发他们“求知”的欲望。例如讲等比数列前n项和公式时，我先给学生出示了一个国际象棋的棋盘，然后讲了一个国王赏麦的故事：相传古印度宰相达依尔发明了国际象棋。当时的国王大为赞赏，就问他想要什么。达依尔说：“请在棋盘的64个方格上，第一格放1颗麦粒，第二格放2颗麦粒，第三格放4颗麦粒，依次类推，每一格放的麦粒数都是前一格的两倍，直到第64格，请您给我足够的麦粒以实现上述要求。”国王觉得这并不是很难办到的,就欣然同意了他的要求。这时，我启发学生想：“国王要给达依尔多少麦粒？”结果学生通过观察很快就找出答案。各个格子里的麦粒数依次是：1，2，22，23，…，263，于是发明者要求的麦粒总数就是1+2+22+23+…+263，接着引导学生把上面的问题看成是等比数列 1，2，22，23，…，263的前64项的和，同时，请学生大胆预测麦粒的重量将是多少？产生悬念,然后一步步引导学生推导出等比数列的前n项的和公式。在公式推导后让学生运用公式算出发明者要求的麦粒总数是：18446744073709551615（粒），重约 7000亿吨。这样，首尾呼应，既培养了学生的观察能力，又激活了学生学习数学的兴趣，同时也让学生明白数学和生活息息相关，把学以致用的思想渗透到课堂中。

二、增强观察的目的性，提高学生的观察能力

观察是思维的触角，是思维的前提，不懂得观察就不懂得思维，要培养学生严密的逻辑思维能力，就必须教给学生观察的方法。数学中有许多概念是由生产生活中的实际模型抽象出来的，因此这一类的概念教学中，教师要通过演示，展示生产生活中的实际模型，尽可能地让学生通过观察概括出其本质属性。

例如：在数列极限概念的教学中，我采取的做法是：首先引导学生观察电脑动态演示做圆的内接正三边形、圆的内接正六边形、圆的内接正十二边形、圆的内接正二十四边形、圆的内接正四十八边形…，（重复三次），然后提出问题：随着圆内接多边形边数的增加，圆内接多边形与圆之间,圆内接多边形的周长与圆的周长之间存在什么样的关系。这时学生会在观察的基础上回答出：随着圆内接多边形边数无限增加，圆内接多边形越来越贴近圆，圆内接多边形的周长越来越接近圆的周长。这时，我再总结以下的结论：设圆的半径为R，圆内接正三角形，正四边形，正五边形…，正n边形的周长所组成的数列 P3，P4，P5，…，Pn，…，则随着圆内接多边形边数n无限增大，圆内接多边形的周长Pn无限地趋向于圆的周长2πR。同时告诉学生：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣。”这种方法就是三国时的数学家刘徽提出的“割圆求周”的方法。从而激发学生的民族自尊心和爱国主义思想情感。接着引导学生把上面的问题看成是无穷数列的项数n无限增大时,数列是否无限地趋近一个常数C的问题。从而引出数列极限的定义。这样进行概念教学，将使学生从认识上初步完成实验——观察——感性——理性的认识过程，从而调动学生学习的积极性，让学生的感知活动按预定的方向和目标进行，使他们从被动地接受任务进行观察转变为主动地、有意识地观察，增强了观察的目的性，也提高了学生的观察能力。

三、边观察边思考，提高学生解决实际问题的能力

思维源于观察，观察是进行思维的基础。只有在观察中思考，在思考中观察，才能唤起联想，进行分析、综合、比较、抽象、概括等思维活动，才能真正理解教学内容，掌握知识，提高解决实际问题的能力。

例如：在二项式定理教学中，二项式定理展开式中各项的系数很难掌握，教学中，我首先提出问题:今天是星期二,再过7天,还是星期二;再过 15天呢?再过 8100天呢?（注:8100=（7+1）100），8100=（7+1）100的展开式是什么呢?联系实际,引发学生了解（a+b）n=?的兴趣。其次，列出学生已掌握的（a+b）0，（a+b）1，（a+b）2，（a+b）3的展开式

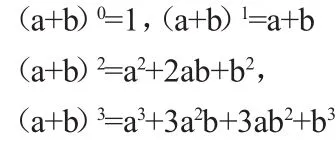
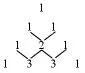
将上述展开式的系数排成三角形如图：

这时让学生观察总结展开式的系数规律，即右图三角形中每行数的规律。学生很快就能总结出：“表中数据除1以外的每个数等于它左右肩上两个数的和”接下来请同学们按此规律排出以下的行为：

右面这个表称杨辉三角，它是宋朝数学家杨辉的杰作，杨辉三角是我国数学发展史上的一个成就。它比欧洲人的帕斯卡三角要早四百多年。

猜想：（a+b）4=?，（a+b）5=?

按照表中数据的规律，不必用多项式乘法，学生就能很快地写出：

并可根据数学规纳法的知识自己推出一般的（a+b）n展开式的系数规律。

总之，现代数学离不开观察，观察可以使我们获得丰富的感性材料，从而为进一步思维、揭示事物的本质规律奠定基础。在数学教学中，只有注重培养学生的数学观察能力，不断教会学生会观察、善于观察，才能不断发展学生的数学思维能力，培养学生良好的思维品质，从而提高学生分析问题、解决问题的能力。

【1】张成恩.数学教学对学生观察能力的培养.中国科技信息，2005年12期.

（作者单位：辽宁城市建设职业技术学院）

（编辑 刘丽娜）