数理方程教学方法探讨

张 瑜

(同济大学数学系,上海 200092)

数理方程教学方法探讨

张 瑜

(同济大学数学系,上海 200092)

旨在通过教学实践体会来探讨数理方程课的教学方法.主要在分析课程特点、挖掘学生学习难点的基础上,从授课内容和思路、理论结合实际、培养学生学习思想、教学手段等多方面论述了提高数理方程课程教学质量的教学方法,同时结合教学实践列举多个数理方程的教学实例来说明锻炼学生能力的途径.

数理方程;教学方法;素质教育

数理方程是大学高年级以及研究生阶段相关专业学习的一门课程,也是学生普遍反应比较难学的一门课程.数学物理方程主要是指从物理学及其他各门自然科学、技术科学中所产生的一些偏微分方程.数学物理方程是纯粹数学的许多分支和自然科学各部门及工程技术等领域之间的一个重要桥梁[1].与高等数学中学习的(常)微分方程相比较,数理方程中未知函数是多元函数,并且存在偏导数,也即数理方程主要研究偏微分方程.

正如前面所提到的数理方程课是一门学生普遍反应比较难学的一门课程,它的理论性强,公式推导比较繁琐复杂,但是该课程也是大部分理工科专业的一门必修课和基础课,地位非常重要.因此本文将结合我们的教学实践就如何上好这门课进行探讨.首先我们将分析数理方程的课程特点和难点,在此基础上我们将结合实践从多个方面分析提高课程课堂教学效果的有效方法.

1 课程特点

数理方程主要培养学生使用数学方法来分析解决物理问题的能力.它的内容比较繁杂,计算比较繁琐,涉及面比较广.其课程特点为：

1.需要的数学知识比较多.

学习数理方程需要对多元函数的微分学有比较好的了解.例如在讲分离变量法时需要用Fourier级数展开;在讲圆形或球形区域混合问题的求解时要用到直角坐标和极坐标或球坐标之间的转换;在讲位势方程Dirichlet问题求解时要用到由高斯公式推出来的 Green公式.

2.需要了解物理背景.

在模型的建立时需要根据实际现象满足的物理定律推出满足的数学模型;定解问题的提出要满足物理规律,不同的定解条件的提出都是有一定的物理意义的.

根据课程特点,学生觉得数理方程难学的原因主要有：

(1)对在高等数学中学习的在数理方程中需要用到的知识掌握的不牢固.

(2)对物理知识的了解不是很清楚.

2 授课体会

1.授课内容、思路.

数学物理方程主要包括波动方程、热传导方程和位势方程.在数学物理方程的授课过程中,我们一般是先推导出三大类经典的方程,然后针对这三大类方程所提出的定解问题,依次讲述求解方法,即行波法、分离变量法、积分变换法和Green函数法.在授课的过程中贯穿由物理规律推出偏微分方程,然后对方程进行求解,最后用解来阐述实际问题的规律,解释物理现象.

2.授课过程紧密结合实际背景.

数理方程是一门和实际物理现象紧密结合的课程,在讲课的过程要时刻结合问题的实际背景来讲解.如(i)在讲解经典方程的导出时,要清楚地阐述所讨论的物理现象,指出该物理现象所满足的物理定律,然后进行适当的数学处理并推导出相应的方程.不同的方程分别对应不同的物理背景,推导出方程的同时要结合实际给学生讲清楚三类方程中的系数和非齐次项的物理含义.(ii)在定解条件的讲解中指出在一维波动方程的边界条件u(0,x)=φ(x)表示初始的位移,ut(0,x)=ψ(x)表示初始的速度;而在一维热传导方程中u(0,x)=φ(x)表示初始的温度分布.(iii)在定解问题适定性内容的讲解中,不应简单的让学生知道定解问题的适定性的概念,而应该紧密的联系实际工程背景来讲解,可举人造卫星的运行轨道的例子使枯燥的内容生动起来.(iv)在讲解完分离变量法之后可以举下面波动方程混合问题的例子

来锻炼学生对分离变量法求解步骤的理解,并用该方程的级数解来阐述说明波的共振的物理现象. (v)为了使学生很好地掌握解的物理意义,可以在讲完行波法和对称延拓法之后,举下面的例子：

例1求解半无界问题

根据行波法是左行波和右行波的叠加的物理意义,可以很快的把该定解问题的解求出来为

通过演示这样的例子的求解,加深学生对行波法物理意义的理解.

3.注意培养学生学习数学思想.

数理方程的教学不仅在于教授学生知识,更在于数学思想的培养.在教学过程中要注意介绍将复杂问题简单化的数学思想.例如线性偏微分方程的叠加原理以及齐次化原理都是将不会解决的问题化为已经会解决的问题;积分变换法是将偏微分方程变换为常微分方程来求解.

4.注意培养学生思考、联想和知识应用的能力.

知识的应用是很重要的,学以致用是学习的最终目的.在数理方程的授课过程中要注意培养学生思考和知识应用的能力.可以对同一个问题采取不同的分析求解方法,如一维波动方程Cauchy问题的D’A lembert(达朗贝尔)公式可以先用行波法(求通解的方法)推导出该公式,在讲Fourier积分变换时还可以用Fourier积分变换将D’A lembert(达朗贝尔)公式推导出来.

同样同一方法也可以用来求解不同问题,如在讲了非齐次波动方程Cauchy问题的Duhamel齐次化原理之后可以举下面的例子锻炼学生对Duhamel齐次化原理的应用.

例2求解波动方程Cauchy问题

在课堂上我们可以用D’A lembert(达朗贝尔)公式结合齐次化原理得到该定解问题的解为

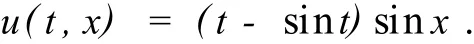
在讲解完这个例子可以给学生提一个问题：既然偏微分方程可以用齐次化原理来求解,那么是否还有别的方程也可以用齐次化原理来求解呢?

在同学们思考之后,可以给出下面的例子：

例3求常微分方程的y″(x)-5y′(x)+6y(x)=ex的通解.

然后让学生思考这两个问题可以用什么方法来求解,齐次化原理是否可以用来求解这两个问题,如果可以的话求解的过程又是如何的.可以在课堂上先提出这样的问题,然后再来演示求解的具体过程,用齐次化原理将例3和例4的解求出来,并和用其它方法求出来的解进行对照.最后让学生们思考有哪些问题可以用齐次化原理来求解,求解的具体步骤有哪些.

通过这样的教学方式,可以使学生将正在学习的数学物理方程和以前学习的常微分方程联系起来,触类旁通,可以更好的掌握课程的核心内容,从而达到良好的教学效果.

5.对不同的内容采用不同的教学手段.

数理方程的课程教学既可以采取传统的粉笔结合黑板的教学手段：板书,也可以采用现代的多媒体教学手段：PowerPoint幻灯片.采用板书的优点是学生易于跟上老师的上课速度;缺点是比较繁琐的公式推导如Bessel方程的求解写在黑板上需要的时间较长.采用幻灯片的优点是可以节省下写较长的定理以及繁杂冗长的公式推导的时间,显示图片图形比较直观准确,一节课的授课内容可以较多一点;缺点是要在授课时注意放映的速度,否则学生会很容易跟不上老师的上课速度.

笔者认为数理方程的课堂教学可以将两种方式结合起来,也就是幻灯片结合板书,对不同的教学内容采用不同的教学手段.可以在幻灯片上投影比较长的定理和比较繁琐的公式推导,证明可以只投影关键点.比较简单的例子等可以用板书,这样在课堂上可以节省时间,能够多介绍数学思想,从而提高课堂教学效率.

最后,在数理方程的教学过程中要注意素质教育内容的融入,注重培养学生的创新能力,培养学生抽象思维能力、逻辑推理能力和分析解决问题的能力.数理方程的教学不仅在于教授学生知识,更在于培养学生的数学思想,提高学生的综合素质,促进学生的全面发展.

[1] 谷超豪,李大潜,陈恕行,郑宋穆,谭永基.数学物理方程[M].北京：高等教育出版社,2002.

[2] 车向凯,谢彦红,缪淑贤.数理方程[M].北京：高等教育出版社,2006.

[3] 刘庆华,韩云端.提高数学教学课堂效果的几点思考[J].大学数学,2005,21(5)：12-14.

Discussion on the Teaching Methods for Equations of Mathematical Physics

ZHANG Yu
(Department of Mathematics,Tongji University,Shanghai 200092,China)

Basing on the teaching experiences of the author,the teaching methods fo r Equations of Mathematical Physics is discussed in this paper.First the characteristic of this course are analyzed,the learning difficulties of this course are excavated.Then ways of how to imp rove the teaching quality are p rovided from some aspects such as teaching thought,integrate theo ry w ith p ractice,train the students learn the ideas,teaching app roach and so on.A number of teaching examp les are also p resented in this paper to illustrate the way of how to imp rove the ability of the students.

equationsof mathematical physics;teaching method;quality education

O175.2;G424.1

C

1672-1454(2011)05-0172-03

2011-01-29