4n阶标准二次幻方的构作

潘凤雏

(1.中国地质大学(北京)地球科学与资源学院,北京 100083; 2.西藏地质调查院,拉萨 850000)

4n阶标准二次幻方的构作

潘凤雏1,2

(1.中国地质大学(北京)地球科学与资源学院,北京 100083; 2.西藏地质调查院,拉萨 850000)

给出标准二次幻方及等重集的概念.利用2n阶正交截态拉丁方,Z4n={0,1,…,4n-1}的对称2次等幂和等分(划分)以及方阵的简单变换构作了4n(n≥2,n≠3)阶标准二次幻方.由于n=3时,存在12阶标准二次幻方,而n=1时,不存在4阶标准二次幻方,故4n阶标准二次幻方的存在性已经完全解决.

标准二次幻方;等重集;正交截态拉丁方

1 引 言

二次幻方的研究可以追溯到法国人Pfeffermann于1890年构作的如下幻方[1]：

该方阵具有8行8列及2条对角线的和为260,而平方和为11180的奇特性质,从而开了高次幻方研究的先河.由此,自然引出了如下定义:

定义1.1称由n2个整数(不一定不同)构成的n阶矩阵为n阶广义二次幻方,简记为BMS(n),如果其n行、n列及两条对角线上的n个元素的和为定值S1而平方和为定值S2.若广义幻方由n2个连续整数构成,则称其为正则的;若正则二次幻方由不大于n2-1的所有非负整数构成,则称其为标准的,记为SBMS(n).称S1(S2)为一次(二次)幻和.

显然,1阶二次标准幻方总存在.为方便,还需要如下定义:

定义1.2若多重集M的元素组成的集合S的任一元素在M中的重复次数均为r,则称M为等重集或r-重集,记为M=r·S.

100多年来,学者们在标准二次幻方的研究上取得了大量成果[1-4].已知结果如下:

定理1.3[1]若n∈{2,3,4,5,6,7},则不存在SBMS(n).

定理1.4[1,2]若n=1或8≤n≤64,则存在SBMS(n).

在另文中,我们将证明

定理1.5设N为正整数,若存在m∉{1,2,3,6}使得m|N,(N/m)∉{1,2,3,6}且m+N/m为偶数,则存在SBMS(N).

本文进一步给出4n阶标准二次幻方的简单而统一的构作,即证明如下主要结果：

定理1.6若n≥2为正整数,则存在SBMS(4n).

在本文中,约定m,n为正整数,矩阵的下标从0开始,Zn表示集合{0,1,…,n-1}.

2 几个引理

引理2.1[5]若n∉{2,3,6},则存在n阶正交对角拉丁方.

因此,n∉{2,3,6}时存在n阶正交截态拉丁方.

引理2.2设n≥3,d0,d1,…,dn-1为任意复数,且c满足

引理2.3设n≥2,c=4n-1,ai(i∈Z4n).由

确定,则

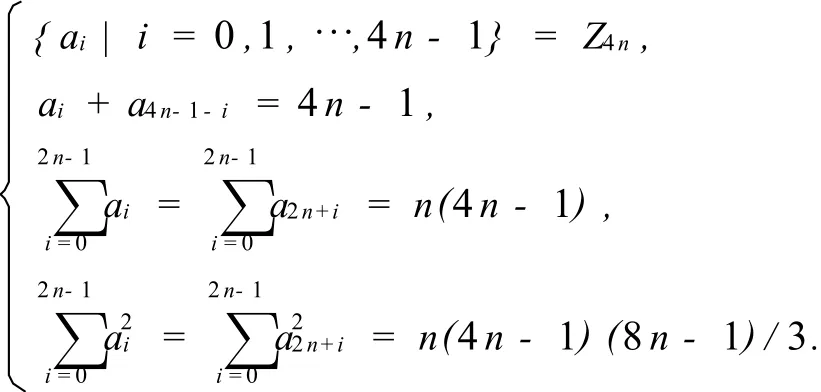
证 由引理2.2易证.

引理2.4设a,b,c为任意复数,则

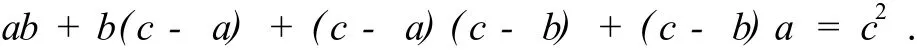
引理2.5设n≥2,ai∈Z4n(i∈Z4n)由引理2.3确定,bi∈Z4n(i∈Z4n),由

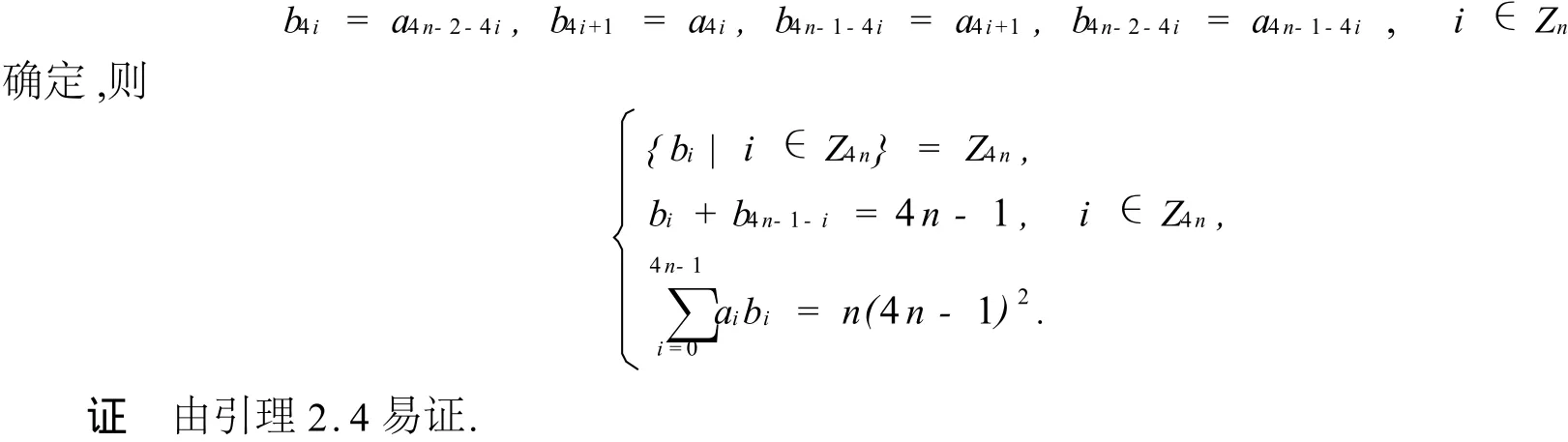
3 主要结果的证明

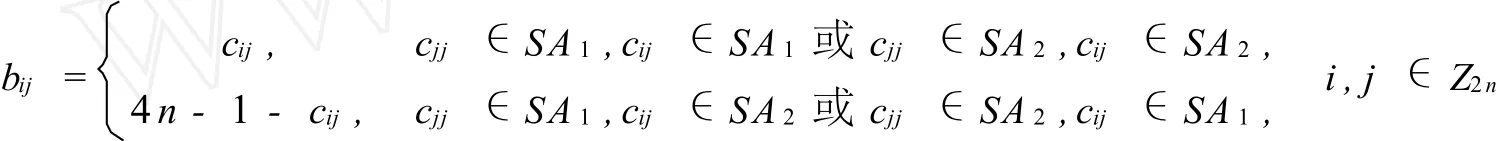
本节,总设ai,bi的意义同于引理2.3和2.5.为方便构作,还需要定义如下一些矩阵.设

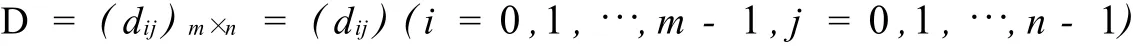
为任意矩阵,记

其中a为任意常量.两个m×n矩阵D和E叠合后形成的阵列记为(D,E).再记

定理3.1设m=2n,n≥2,n≠3,A=(aij)m×m为SA1上的截态拉丁方且aii=ai(i∈Zm),C=(cij)m×m为SB1上的截态拉丁方且cii=bi(i∈Zm).再设A与C正交,B=(bij)m×m由

确定.那么,

(3.1.1)A与B正交;

(3.1.2)B的任一行的2n个元素两两不等且两两之和不为4n-1.

(3.1.3)B的任一列的2n个元素的集合为SA1或SA2.

证A,C的存在性由引理2.1所保证.显然,C的位于不同列的与A的同一元素对应的2n个元素b0,b1,…,b2n-1的每一个bi在B中的相同位置的元素只能为bi或4n-1-bi之一,因此,B的这2n个元素中的任意两个不等且和不为4n-1,否则推出j≠i∈Z2n时bi=bj或bi+bj=4n-1,这是矛盾.故A与B正交.同理,C的任一行的2n个元素b0,b1,…,b2n-1的每一个bi在B中的相同位置的元素只能为bi或4n-1-bi之一,因此(3.1.2)成立.因

故由B的构成可知(3.1.3)成立.

定理3.2设m=2n,n≥2,n≠3,A,B由定理3.1构作,简记AC‖4n-1‖为AS,BC‖4n-1‖为BS.再设

则 P为4n阶标准二次幻方.

证 显然

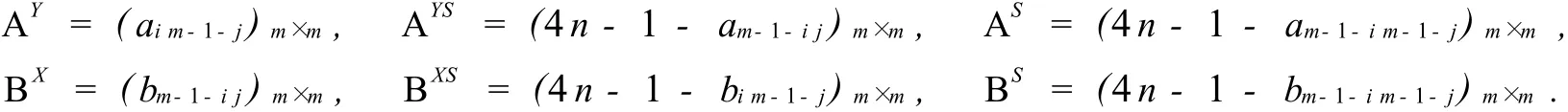
先证G与H正交.若(AY,BXS)中存在两个位置(i,j)和(k,l)使

则aim-1-j=akm-1-l且bim-1-j=bkm-1-l.由于A与B正交,故i=k,j=l.这说明(AY,BXS)中没有相同元素.同理可证(AYS,BX)及(AS,BS)中没有相同元素.若(A,B)和(AY,BXS)中有相同元素,则存在两个位置(i,j)和(k,l)使

故得bij+bkm-1-l=4n-1.因B中任意两个元素之和不为4n-1,故导致矛盾.同理可证(G,H)中的其余位置的元素也是两两不同的.

由于 G和H的元素均属于Z4n,故 P由0,1,…,16n2-1的所有元素组成.

次证G和H为广义二次幻方.因G的每列和两条对角线上元素之集均为Z4n,故每列和两条对角线上元素之和为n(4n-1)而平方和为n(4n-1)(8n-1)/3.因AY为A的Y轴镜像映射矩阵,AYS为AS的Y轴镜像映射矩阵且AS为SA2上的截态拉丁方,故 G的每行元素组成的多重集为2·SA1或2·SA2,故由引理2.5知每行元素之和为n(4n-1)而平方和为n(4n-1)(8n-1)/3.同理,因 H的每行和两条对角线上元素之集均为Z4n,故其上元素之和为n(4n-1)而平方和为n(4n-1)(8n-1)/3.再由定理3.1中的(3.1.3)知 H的每列元素组成的多重集也为2·SA1或2·SA2,故G和H为广义二次幻方.

再证 G和 H对应元素乘积构成的矩阵(记为[GH]=(gij hij)4n×4n)为广义幻方(每行、每列及两条对角线上元素之和为定值).分四种情况证明.

(a)主对角线

确定,则将上述构作方式稍微变换,可构作元素互异的k≥2时的BMS(4k+2).

4 例 子

举8阶标准2次幻方的构作为例.仿照引理2.3和2.5的方法,可构作四个集合如下：

由此可构作两个正交的对角拉丁方A,C和方阵B如下:

再由定理3.2可构作方阵G,H,P如下:

易于验证 P为8阶标准2次幻方且具有中心对称性质.

[1] Christian B.Multimagic squares[DB/OL].http：//www.multimagie.com.

[2] 高治源.平方幻方[DB/OL].http：//www.zhghf.net.

[3] 李立.用正交拉丁方构造两次幻方[J].数学季刊,1990,5(4)：95-101.

[4] 鲁思顺.2m(2n+1)2阶平方幻方的构作方法[J].山东师大学报(自然科学版),1991,6(2)：117-120.

[5] Brow n JW,Cherry F,Most L,et al..The spectrm of orthogonal diagonal Latin sqares[M].Rees R S.Graphs, Matrices and Designs.New Yo rk：Marcel Dekker,1993：43-49.

O157

A

1672-1454(2011)05-0103-05

2008-06-10