TiO2/ZnO纳米薄膜界面热导率的分子动力学模拟*
2011-11-02杨平吴勇胜许海锋许鲜欣张立强李培
杨平吴勇胜许海锋许鲜欣张立强李培
TiO2/ZnO纳米薄膜界面热导率的分子动力学模拟*
杨平吴勇胜 许海锋 许鲜欣 张立强 李培
(江苏大学机械工程学院,镇江212013)
(2010年7月5日收到;2010年9月28日收到修改稿)
采用平衡分子动力学方法及Buckingham势研究了金红石型TiO2薄膜与闪锌矿型ZnO薄膜构筑的纳米薄膜界面沿晶面[0001](z轴方向)的热导率.通过优化分子模拟初始条件中的截断半径rc和时间步后,计算并分析了平衡温度、薄膜厚度、薄膜截面大小对热导率的影响.研究表明,薄膜热导率受薄膜温度和厚度的影响很大,当温度由300 K升高600 K时,薄膜的热导率逐渐减小;当薄膜厚度由1.8 nm增大到5 nm时,热导率会逐渐增大;并在此基础上对更大厚度范围内TiO2/ZnO界面热导率可能变化性态进行了探讨.
热导率,分子动力学,TiO2/ZnO纳米薄膜界面,数值模拟
PACS:66.70.Df,83.10.Rs,68.35.-p,02.60.-x
1.引言
近年来,纳米科学特别是纳米材料的制备和性能研究引起研究者的广泛关注.这是由于当材料小到纳米尺度时,处于材料边界处的原子在组成整个纳米材料的原子中占有很大的比例,这样的结果就体现为纳米材料的尺寸效应.另一方面,界面作为微纳制造中最普通的结构,对材料的力学、电学、热传导等物理和化学特性具有非常重要的影响.在界面附近,材料的物理和化学性质有可能发生很大的变化,这就体现为纳米材料的界面效应.因此,界面结构及界面效应研究的重要性是不能忽略的,界面科学在材料和物理研究领域中已成为一个新的分支[1].由于尺寸效应和界面效应的影响;纳米薄膜界面传热等相关问题甚至需要从分子/原子的层面来进行研究[2].而分子动力学方法(molecular dynamics,简记为MD)就是通过求解有相互作用的各个粒子的运动方程,得到每个粒子的空间位置、运动状态随时间的演化状况,从而统计出材料的宏观行为特性的方法.前期的研究显示了MD在研究微/纳尺度传热特性方面的可行性;如吴国强等[3]采用平衡分子动力学方法(EMD)和非平衡分子动力学方法(NEMD)模拟了氩晶体薄膜的法向热导率,发现热导率随着薄膜厚度的增加而呈线性增加,贾明等[4]则采用改进分析型嵌入原子模型(MAEAM),通过MD来模拟了Mo薄膜的热力学性质.侯泉文等[5]通过NEMD研究了碳纳米管热导率与长度的关系,发现碳纳米管热导率随其长度的增加而增加;并详细研究了导热中弹道运输阶段、扩散运输阶段与碳纳米管长度的关系.Kulkarni和Zhou[6]利用MD模拟了长度从19—41(1= 0.1 nm)的ZnO纳米带在温度范围为500—1500 K,沿[0110]方向上的热导率,研究显示ZnO纳米带具有明显的尺寸效应和温度效应.Hegedus[7]应用NEMD讨论了异质系统界面热传导,并与基于声子散射理论的界面热阻模型进行了比较,两者取得了良好匹配.Liang和Sun[8]采用NEMD发现,界面热阻在纳米界面结构热传递中非常重要,并详细讨论了界面特性对热导率的影响.Volz等[9]采用NEMD模拟研究了界面、晶格应变对整个Si/Ge超晶格热导率的影响,并且模拟结果与实验数据相符;另外,Yang等[10,11]则采用MD与有限元结合的方法研究了两种材料所形成的界面对热传输的影响.
过渡金属氧化物因其具有良好的光电磁等特性而成为了当今研究的热点.ZnO和TiO2作为过渡金属氧化物中很常见的两种物质,在太阳电池和光催化剂中有着广泛的应用,但对这两种物质特别是两者构筑的界面结构在纳米尺度上的传热特性和机理还缺乏足够的了解.本文采用EMD及优化的Buckingham势函数来研究金红石型TiO2与闪锌矿型ZnO构筑的纳米薄膜界面特性,研究在xy平面上晶胞数目、整个薄膜系统的厚度以及系统温度与热导率的关系.
2 .建模与计算
在建模时,首先必须设置原子的初始位型,原子的初始位型包括在t0时刻速度以及其他运动信息,这些运动属性可描述为

原子i上受到的合力为MD势函数负的梯度,即
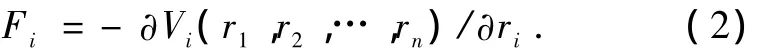
通过数值求解牛顿方程得到一个时间序列,即可得到任意物理量的系综平均为

因此,从计算数学的角度来看,MD是微分方程的数值解问题.
对于系统温度保持不变的正则系统(NVT),采用Nose-Hoover热浴进行温度调节,描述该系统的运动方程为

其中mi,ri,fi,pi和U(r1,r2,…,rn)分别是第i个粒子的质量、坐标、所受到的合力、动量和其他粒子对其的作用势,ξ是约束温度不变的参数.由于温度不变,系统动能=0的关系,所以参数
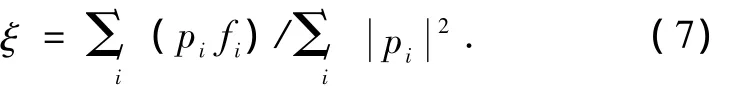
2.1.局域温度的量子修正
在经典分子动力学中,系统温度由Boltzmann能量均分定理得到

其中N为模拟区域的粒子总数,kB为Boltzmann常数,TMD为系统模拟温度,mi和vi分别为粒子的质量和速度.当温度低于材料Debye温度时,由于系统的比热容与温度有关,(8)式不再成立,即系统实际温度T≠TMD.为了获得正确的仿真结果,必须对模拟温度TMD、模拟结果kMD进行量子化修正.采用Debye模型进行温度统计的量子修正,通过求解下列积分方程进行修正

求解此方程可以得到与MD的局域温度Tj,MD相对应的真实晶格温度Tj,而求解方程(9)须引入晶格格波谱,即格波波矢q与频率ω的关系.本文采用近似的Debye模型

Debye模型给出的晶格热容为

其中C'v为质量定容热容,ΘD为Debye温度.在Debye近似下,能量方程(9)转化为
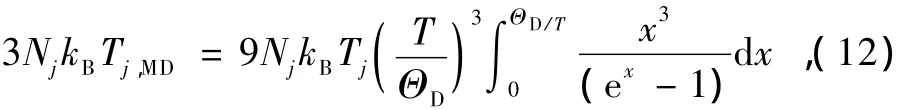
本文通过求解方程(12),实现了对MD得到的局域温度的量子修正.
2.2 .EMD中热导率的计算
EMD意味着通过模拟系统的平衡态求出导热系数.从温度梯度加上到形成稳态的过程中,热流的变化有可采用如下公式描述[12]:

其中τ是声子的弛豫时间,q是稳态的热流,qz是到达稳态前在z轴方向随时间变化的热流,且
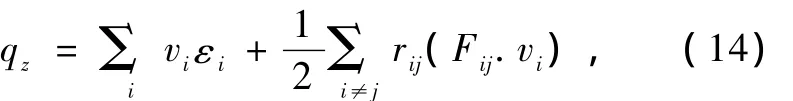
其中,εi是包含势能和动能的总能量.(14)式只适用于两体势.
采用平衡态方法时,没有宏观的温度梯度,所以q=0.根据G-K公式,热导率可以由热流qz(t)的自相关函数积分得到[13]
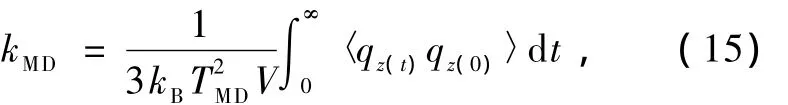
其中kMD为热导率,T为温度,V为模拟区域的体积.
2.3.原子之间的作用势函数
在MD模拟中,材料系统内粒子间相互作用是通过势函数来实现,势函数的选择直接关系到模拟结果的准确性.氧化物与氧化物组成的薄膜界面原子之间的作用力,还没有成熟的势函数来描述[14].本文中的TiO2/ZnO薄膜界面系统,原子作用对存在10种类型.这里将采用Buckingham势函数的两体势形式来描述TiO2及ZnO薄膜内部原子之间的作用力,Buckingham函数形式[15]如下:
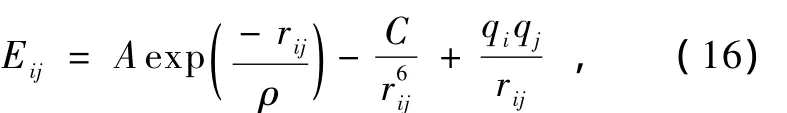
其中Eij为原子i和j的相互作用能.对于ZnO和TiO2中原子的A,C,ρ的取值见文献[15,16];对于ZnO薄膜和TiO2薄膜界面上的原子作用对如Ti-Zn,Ti-OZn,Zn-OTi,OZn-OTi,本文将采用文献[17,18]中方法来处理.
2.4.模型的建立
本文研究的TiO2,ZnO的晶体类型分别为金红石型和闪锌矿型,晶体结构如图1所示,它们的参数如下:TiO2的参数为密度ρ=4.25×103kg/m3,晶胞参数a=4.59,c=2.96;Zn O的参数为密度ρ=5.45×103kg/m3,晶胞参数a=4.63.
模型建立过程如下:本文模拟的是TiO2/ZnO沿晶面[0001]的热导率,在xy平面上将采用4×4个晶胞,且xy平面平行于晶面[0001],在z方向上对TiO2/ZnO薄膜界面建立了1.8,2.9,3.9,5 nm的4个厚度.建立的模型如图2所示.

图1 晶体结构示意图(a)TiO2晶体晶胞结构;(b)ZnO晶体晶胞结构

图2 TiO2/ZnO薄膜界面模型
2.5.MD的初始条件
在x,y方向上采用周期性边界条件,z轴为热流方向,采用Nose-Hoover热浴进行温度调节,模拟在正则系统(NVT)中进行,采用Gear算法进行运动方程积分,库仑力的计算采用Ewald方法,时间步长为0.1 fs,TiO2中原子Ti和O的价位数分别为+2.196和-1.098,ZnO中原子Zn和O的价位数分别为+2和-2.
MD初始条件中的另外两个参数截断半径rc和模拟时间步数是两个很重要的初始条件,对模拟结果和计算时间有着直接的影响.为了保证模拟结果的精度和尽量减少计算时间,下面通过计算来确定这两个参数的大小.
2.5.1 .模拟时间的确定
由于文中是通过EMD来计算1.8,2.9,3.9,5 nm这4个厚度的薄膜在温度为300,400,500,600 K下的热导率,所以可以通过系统平衡温度与模拟时间的关系来确定MD模拟时间的大小,即当系统温度平衡时所对应的时间即为我们所需要的MD初始时间.图3中(a)—(d)中的曲线分别表示的是TiO2/ZnO薄膜界面厚度为3.9 nm时,在模拟温度为300,400,500,600 K下薄膜界面的平衡温度与模拟时间的关系,此处分子模拟的初始条件中的rc= 10,模拟时间为20 ps(时间步长为0.1 fs,步数为2×105).从图3可以看出,不管在哪个模拟温度下,系统温度平衡的时间大约都在10 ps(1×105步)左右,在10 ps后,系统温度基本不变,即整个薄膜系统达到平衡.因此,温度对平衡时间没有太大影响,我们就把10 ps(1×105步)当做MD的初始时间.
2.5.2 .截断半径rc的确定
在确定模拟时间为10 ps的情况下,再来考虑rc大小的选择,为了消除其他因素的影响,此处选择的薄膜系统及初始条件与上述相同,只是此时的变量为rc.计算结果如图4所示,模拟结果显示出同一薄膜系统不同温度下rc的选取对模拟结果影响各不相同,如模拟温度为300 K时,可选取0.4 nm及以上的长度为rc,而600 K时则要选取0.6 nm及以上的长度为rc才能保证模拟结果的精度.但不管在哪个模拟温度下,当rc为0.6 nm时,计算出来的热导率已具有足够的准确性.为了保证模拟结果的精度和减少计算时间以及满足不同的薄膜系统,本文将设rc=0.6 nm作为MD的初始条件.

图3 薄膜界面平衡温度与时间关系曲线(a)T=300 K;(b)T=400 K;(c)T=500 K;(d)T=600 K
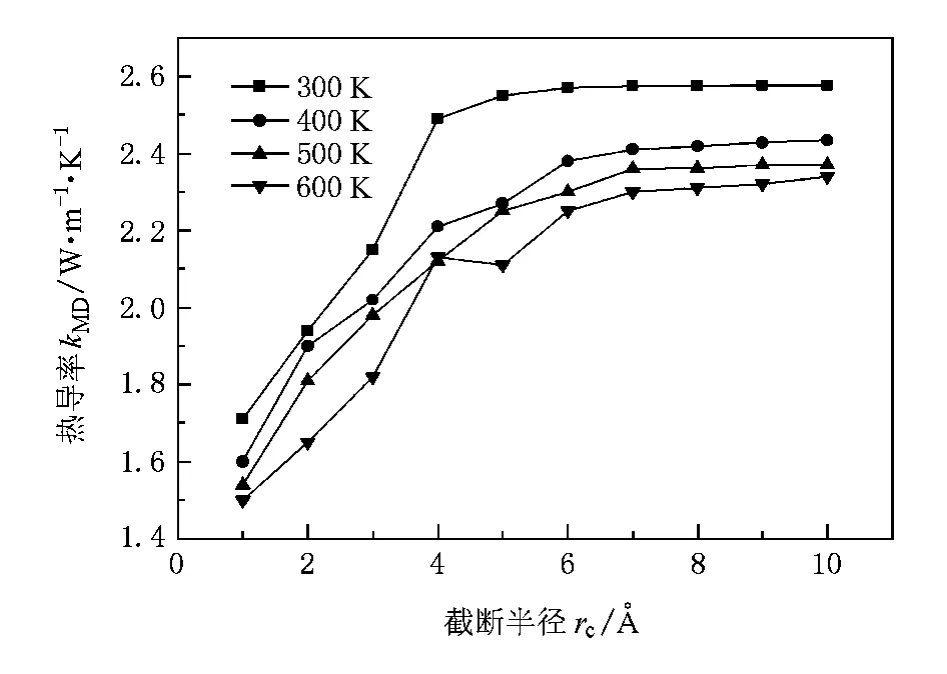
图4 热导率随着截断半径的变化
由于上述两个参数在确定过程中只考虑了温度因素,而本文在模拟过程中存在4种不同厚度,因此在进行计算前先对上述确定的两个参数进行论证以确定它们的正确性.图5计算的是在系统温度为400 K,TiO2/ZnO薄膜界面厚度为1.8,2.9,3.9, 5 nm情况下热导率与时间的关系曲线.从图5可以看出,不管哪一个厚度下,当模拟时间大于10 ps时,热导率的变化已经很小.这与上面用温度来确定的模拟时间步是一致的,并且时间步数的选择与薄膜界面厚度没有太大的关系.因此,上述确定的两个参数是可靠的.
3 .模拟结果与讨论
3.1 .TiO2/ZnO薄膜界面水平方向尺寸与热导率的关系
图6显示的是TiO2/ZnO薄膜界面在厚度为5 nm时水平方向尺寸对热导的影响.从图6可以看出,随着水平尺寸的增大(原子数的增多),薄膜界面热导率也随之增大.这说明薄膜在水平方向也具有明显的尺寸效应.可能的原因是水平尺寸越大,薄膜的热阻越小,而热导率与热阻之间存在反比关系,因而水平尺寸越大,热导率也越大.这与文献[19]的结果相符.另外,从图6还可以看出,原子数增多时,计算结果的波动越来越小,即精度得到很大的提高.这是因为截面积的增加,模拟的原子数相应增加,这就更接近于实际情况,因而模拟得到的结果也就更接近.由此可知,要想得到精度高的模拟结果,选择合适的水平尺寸是必要的,这也是本文中选择4×4个原胞进行模拟的原因.

图5 不同厚度下热导率与模拟时间的关系

图6 水平方向模型尺寸对热导率的影响
3.2 .TiO2/Zn O薄膜界面厚度及温度与热导率的关系
图7显示了不同温度下TiO2/ZnO薄膜界面沿z轴方向的尺寸对薄膜热导率的影响.从图7可以看出,TiO2/ZnO薄膜界面热导率随厚度的增加而增加,并且随着厚度增加,热导率增加趋势变得平缓.模拟得到的界面热导率处于1.95—2.78 W/mk的范围内,这不仅远小于对应的单层TiO2薄膜或ZnO薄膜的热导率(TiO2薄膜热导率为4 W·m-1·K-1左右[20],ZnO薄膜热导率为10 W·m-1·K-1左右[6]),而且也小于这两种薄膜材料热导平均值的一半,这一结论与文献[21]相符.这种薄膜尺寸效应以及小于两种薄膜热导率平均值一半的原因可作如下解释.
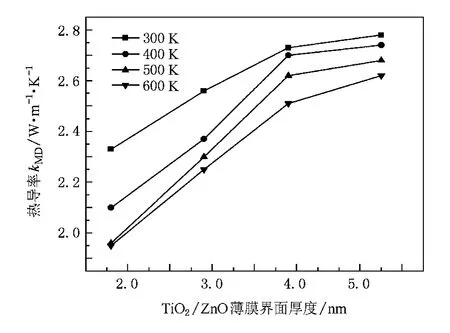
图7 薄膜界面厚度对热导率的影响
对于半导体材料而言,声子是主要的热载流子.组成TiO2/Zn O薄膜界面的单层薄膜中,根据固体物理理论中声子气的动力论,电介质固体的晶格导热系数可表示为

其中v为声速,l为声子的平均自由程.经典固体物理理论中认为:尺寸效应一般在薄膜厚度小于声子平均自由程的情况下发生.在本文模拟的温度范围,声子平均自由程可近似表示为

其中γ为Gruneisen常数,通常γ≈2,Tm为材料熔点温度,a为晶格常数.对于TiO2和Zn O两种材料而言,通过(18)式可以估算出它们的平均声子自由程为10 nm以上.这要大于本文研究的薄膜厚度.因而整个薄膜界面显示出尺寸效应.
另外,在组成TiO2/Zn O薄膜界面中的单层薄膜内部,薄膜边界的散射对热导率也有很大影响,根据晶格导热系数理论,可得到晶格导热系数为
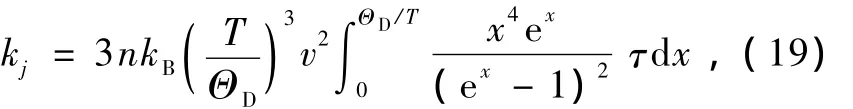
其中n为原子的数密度,τ为声子平均弛豫时间.由于薄膜边界对声子的散射,薄膜中有效的声子平均弛豫时间可根据Matthiessen法则确定,

其中τb为块体材料中的声子平均弛豫时间,p为薄膜边界对声子的镜反射率,d为薄膜的厚度.根据(19)和(20)式可以得出,d和p越大,有效弛豫时间τ也越大,从而薄膜热导率就越大,反之就越小.这就是热导率随着薄膜厚度的增加而变大的原因.
对于TiO2/ZnO薄膜界面而言,声子在传热过程中除了在薄膜内部和边界发生散射外,界面处对声子的影响也非常大.声失配理论认为,声子像平面波一样是连续体,当通过两种不同的材料时声子会在界面处发生反射、散射以及模转化,从而导致声子传热能力的降低.因此,整个薄膜界面的热导率不但小于单层薄膜的值,而且要小于两层薄膜热导率平均值的一半.

图8 TiO2/ZnO薄膜界面热导率与温度的关系
图8 所示为TiO2/ZnO2薄膜界面热导率与温度的关系.从图8可看出,当温度由300 K上升到600 K时,热导率降低了15%左右,显示出薄膜热导率具有明显的温度效应.这主要是由于温度升高时,材料的热软化以及原子振动幅度变大,以致高频声子在热传递中起的作用越来越大,而高频声子的散射更强,声子自由程更短,从而导致整个薄膜界面热导率降低.据文献[20]中对TiO2单层薄膜和文献[6]中对ZnO单层薄膜热导率的实验研究可知,在一定的温度范围内,单层TiO2薄膜和单层ZnO薄膜热导率随着温度的增加而减小.本文的研究结果也表明,TiO2/Zn O薄膜界面热导率随温度的变化趋势和其单层薄膜随温度的变化趋势具有相似性.
4 .结论与讨论
通过计算,选择合理的截断半径rc=0.6 nm和模拟时间t=10 ps,用EMD对TiO2/ZnO薄膜界面热导率进行了模拟.模拟结果表明:薄膜界面热导率在水平方向和沿晶面[0001]方向都存在明显的尺寸效应,在水平方向上晶胞数位4×4时的热导率几乎为1×1晶胞热导率的2.5倍.晶面[0001]方向上,薄膜界面厚度为5 nm时的热导率比1.9 nm时高出约20%,并且整个TiO2/ZnO薄膜系统热导率值要小于这两种材料热导率平均值的一半.其次,晶面[0001]方向的热导率还具有明显的温度效应,热导率随着温度的升高而减小,减小幅度达到15%.
对于更大范围的TiO2/Zn O薄膜界面厚度与热导率的的关系,用于计算容量的限制,本文未作进一步的研究,但进行以下两种推测:1)随着TiO2/ZnO薄膜界面厚度的增加,其热导率也随着增加,最终直至宏观TiO2与宏观ZnO所成界面的热导率.2)随着薄膜厚度的增加,热导率变化有不可预测性,如出现反向非线性等.若为第二种推测,则说明TiO2/Zn O薄膜界面热导率具有特殊性.这一特殊性是普遍存在于氧化物界面之间,还是只有TiO2/Zn O薄膜界面所特有?这有待进一步探索.
[1]Allara D L 2005 Nature 437 638
[2]Chou F C,Lukes J R,Liang X G 1999 J.Heat Transfer.10 141
[3]Wu G Q,Kong X R,Sun Z W,Wang Y H 2006 Acta Phys.Sin.55 1(in Chinese)[吴国强、孔宪仁、孙兆伟、王亚辉2006物理学报55 1]
[4]Jia M,Lai Y Q,Tian Z L,Liu Y X 2009 Acta Phys.Sin.58 1139(in Chinese)[贾明、赖延清、田忠良、刘业翔2009物理学报58 1139]
[5]Hou Q W,Cao B Y,Guo Z Y 2009 Acta Phys.Sin.58 7809 (in Chinese)[侯泉文、曹炳阳、过增元2009物理学报58 7809]
[6]Kulkarni A J,Zhou M 2006 Appl.Phys.Lett.88 141921
[7]Hegedus P J,Abramson A R 2006 Heat Mass Transfer.49 4921
[8]Liang X G,Sun L 2005 Microscale Thermophys.Eng.9 295
[9]Volz S G,Saulnier J B 2000 Microelectron.J.31 815
[10]Yang P,Liao N B 2008 Appl.Phys.A 92 329
[11]Yang P,Liao N B 2008 J.Thermophys Heat Transfer 22 581
[12]Zhong Z R,Wang X W,Xu J 2004 Numer.Heat Transfer B 45 429
[13]Schelling P K,Phillpot S R,Keblinski P K 2002 Phys.Rev.B 65 144306
[14]Sinnott S B,Dickey E C 2003 Mater.Sci.Eng.R 43 1
[15]Wunderlich W 1998 Phys.Stat.Sol.A 170 99
[16]Naicker P K,Cummings P T,Zhang H Z,Banfield J F 2005 J.Phys.Chem.B 109 15243
[17]Sergey V D,Nobuhiro Y,Yutaka K 2004 Acta Mater.52 1959
[18]White A 2000 Intermolecular Potentials of Mixed System:Testing the Lorentz-Berthelot Mixing Rules With Ab Initio calculations (Melbourne Victoria:DSTO Aeronautical and Maritime Research Laboratory)p1
[19]Stevens R J,Zhigilei L V,Norris P M 2007 Int.J.Heat Mass Transfer.50 3977
[20]Kim D J,Kim D S,Cho S 2004 Int.J.Thermophys.25 281
[21]Abramson A R,Tien C L,Majumdar A 2002 J.Heat Transfer.124 963
PACS:66.70.Df,83.10.Rs,68.35.-p,02.60.-x
*Project supported by the National Natural Science Foundation of China(Grant Nos.61076098,50875115),the Natural Science Foundation of
Jiangsu Province,China(Grant No.BK2008227),and the Graduate Innovative Program of Jiangsu Province,China(Grant No.CX10 B-252 Z). E-mail:yangping1964@163.com
Molecular dynamics simulation of thermalconductivity for the TiO2/ZnO nano-film interface*
Yang PingWu Yong-Sheng Xu Hai-Feng Xu Xian-Xin Zhang Li-Qiang Li Pei
(School of Mechanical Engineering,Jiangsu University,Zhenjiang 212013,China)
(Received 5 July 2010;revised manuscript received 28 September 2010)
In the paper,the equilibrium molecular dynamics and Buckingham potential function are used to investigate the thermal conductivity of TiO2/ZnO nano-film interface along to[0001](z-axis).The effects of the equilibrium temperature,the thickness and the cross section of the nano-film interface on the thermal conductivity of TiO2/ZnO are investigated by optimizing the cut-off radius(rc)and the time step for initial condition of molecular dynamics.The results indicate that the thermal conductivity of TiO2/ZnO nano-film interface decreases with temperature increasing from 300 K to 600 K,and increases with film thickness increasing from 1.8 to 5 nm.Finally,the relationship between the thermal conductivity and the thickness of TiO2/ZnO nano-film interface is discussed.
thermal conductivity,molecular dynamics,TiO2/ZnO nano-film interface,numerical simulation
*国家自然科学基金(批准号:61076098,50875115)、江苏省自然科学基金(批准号:BK2008227)和江苏省研究生创新计划(批准号: CX10 B-252 Z)资助的课题.
E-mail:yangping1964@163.com
