谈如何增强学生的记忆力

辽宁 商娟

谈如何增强学生的记忆力

辽宁 商娟

记忆方法多种多样，本文从理解记忆、口诀记忆、兴趣记忆、联想记忆、数形结合记忆等方面对如何增强学生的记忆力做了探讨。

增强；记忆力

学习知识的目的在于应用，而牢固地掌握知识是应用的先决条件。加强概念、公式、定理、性质等记忆，提高记忆效率能使数学知识不断地积累和丰富，能进一步引导学生去发现知识，发展智能，从而提高分析问题和解决问题的能力。

加强记忆，从以下几方面着手：

一、理解记忆

理解得透，才能记得牢。理解是记忆的基础。因此在数学教学中加强概念关系和原理的教学，从多方面揭露数学事实、数学概念和原理的本质，通过一定的逻辑体系，使这些知识联系起来，是增强记忆、巩固知识的好办法。

例如，对于移轴公式：

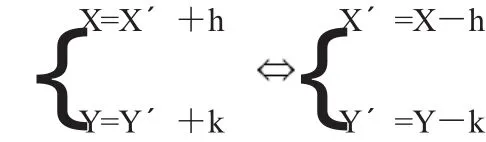
只要记住新原点Oˊ在旧坐标系中的坐标是[h，k]，而在新坐标系中的坐标是[0.0]，上面两个公式中的“+”、“—”号只要分别用（h，k）代（x，y）用(0.0)代(xˊ，yˊ)是不难判定的。

在学习过程中，我们可以充分利用已有的知识和经验，把新知识纳入相应的知识系统中去成为其有机组成部分，这样就可以加深理解，牢固记忆了。

二、口诀记忆

数学理论抽象、繁杂。公式、性质又是多不可数，而对已有的理论，公式，性质的记忆又是学习新知识的基础。把一些相似相近的知识编成顺口溜、口决，记忆起来就较为方便。

例如：将一些难以记忆的公式或规律，如果编成口诀来记忆，效果会更明显些。比如，在三角函数部分中，各象限的角的三角函数值的符号，总结成口诀，记忆起来就方便多了：“一全正，二正弦，三正切，四余弦”。也就是说在第一象限里，各三角函数值全部都是正值；第二象限中只有正弦和它的倒数余割是正值；第三象限，只有正切和它的倒数余切是正值；第四象限只有余弦和它的倒数正割是正值。这样以来，记忆效果最好了。

又如:sin(α+β)=sinαcosβ+cosαsinβ，就采用了这样的口诀:塞扣+扣塞，塞就是sinα，扣就是cosα，同样的cos(α+β)=cosαcosβ-sinαsin β，口诀就变成了扣扣——塞塞,这样把公式的记忆简单化了。

再如：学生对三十六个诱导公式记忆很困难，但口诀“奇变偶不变，符号看象限”便可使记忆很明朗、轻松。其含意为：对角和α的三角函数关系。当K是奇数时的三角函数值等于α的相应的函数值；如正弦与余弦互换，正切与余切互换；当K为偶数时的三角函数值等于α的同名函数值。“变”与“不变”指的是三角函数名称；至于三角函数值的符号，则由K·Л/2±α所在象限的原三角函数的符号来决定。

三、联想记忆

联想，就是由一事物想起另一有关的事物。巴甫洛夫认为：记忆要依靠联想，而联想则是新旧知识建立联系的产物。学习是一种由感性认识发展到理性认识的过程。要全面的掌握客观事物，就要从特殊到一般，从表象到本质，揭露事物间的种种联系，进而形成各种联想，提高记忆效果。具体说，联想分以下几种情况：

1.类似联想。即从性质接近，形状相似的同类事物引起联想。

例如：双曲线与椭圆都是有心二次曲线，它们有十分类似的性质。若能将椭圆的性质记好，在学习双曲线时进行适当的对比，建立起内在联系，找出差别。那么在以后的应用过程中，必然会引起联想。这种记忆很牢固，同时对有心二次曲线也有一个深刻的认识。

2.对比联想。即从具有相反特点的事物引起联想。不同的数学对象有对立的方面，因此可以进行对比，形成认识上的一对对矛盾。于是当矛盾一方出现时，可引起对矛盾另一方的联想。

例如：在学习正弦函数和余弦性质时，可以对它们图象进行对比，这样也可以使性质能在辨析图象的基础上得到一定深度的识记：

（1）正弦函数图象经过原点，而余弦函数不过原点。

3.关系联想。如：在学习三角函数时，sinA与cscA,cosA与secA都是倒数关系，我们可以这样启发学生，弦和割之间存在倒数关系，还有S字母开头与字母C之间互相倒数关系。。此外，等差数列与等比数列的定义及其公式等。都能通过联想、加深理解、增强记忆。

数学知识本来就具有严密的逻辑性，科学的系统性，若能注重知识系统，根据知识间的逻辑关系，循序渐进，逐步深化，就会使新知识不断地纳入学生的知识体系，形成牢固的知识链系。

4.兴趣记忆。在记忆特殊角的三角函数值时，如果教给学生特殊的规律，引发学生的兴趣记忆，效果是事半功倍的。

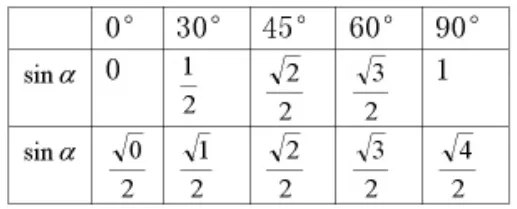
5.数形结合记。用相应的图形来反映数学的抽象，图形可以代替很多词语的内涵，而我们对图形的记忆往往较容易。用这样方法记忆，印象很深刻，也很准确。

再如：圆、椭圆、双曲线之间大致关系，及椭圆、双曲线的大致图形可由下图来判断：

上图含义为：

(1)e=0时，图形为圆；

(2)0

(3)e>1时，图形为双曲线，且随着e的增大，双曲线的两支越来越靠近对称轴。

总而言之，数学中的记忆方法多种多样，若能灵活的掌握和运用，对学好数学会有很大帮助。同时，将几种方法结合起来，常常使知识的掌握更系统、更牢固。知识是无穷尽的，记忆方法更有待于不断的发现，结合自己的知识经验，构造相应的方法，记忆的结果才是最深刻的。

（作者单位：鞍山第二中等职业技术中专）

（编辑 刘丽娜）