负荷模型对电力系统动态稳定的影响①

邹德旭， 贺仁睦， 司大军

(1.华北电力大学与云南电网研究生工作站， 昆明 650217； 2.华北电力大学电气与电子工程学院， 北京 100085； 3.云南电力试验研究院(集团)有限公司， 昆明 650217)

负荷模型对电力系统动态稳定的影响①

邹德旭1， 贺仁睦2， 司大军3

(1.华北电力大学与云南电网研究生工作站， 昆明 650217； 2.华北电力大学电气与电子工程学院， 北京 100085； 3.云南电力试验研究院(集团)有限公司， 昆明 650217)

随着大区电网的互联，低频振荡在我国电力系统中已成为突出的问题。本文研究电力系统的负荷模型对电力系统动态稳定的影响。通过搭建单机无穷大系统，理论上研究送端负荷分别采用恒功率，恒电流及恒阻抗模型时，分析其与自动电压调节器及电力系统稳定器的相互作用对电力系统动态稳定的影响。通过对一个两区域四机系统的典型实例，利用PSD-BPA4.0版中小扰动程序对其进行仿真研究分析，结果表明，当电力系统进安装AVR的情况下，送端负荷采用恒功率模型，更有利于系统的稳定；当系统安装PSS的情况下，送端采用恒阻抗模型更有利于系统稳定。

负荷模型； 动态稳定； 自动电压调节器； 电力系统稳定器

随着电网规模的扩大和大区电网之间的互联，电力系统的小干扰稳定性问题越来越突出。低频振荡在我国电力系统中仍然是突出的问题，并随着我国大区电网互联而更加凸现出来。

电力系统的主要元件有发电机、负荷和电力网络，电力负荷模型对电力系统稳定性的计算结果影响较大[1～5]。文献[6]指出当降低地区负荷对电压的灵敏度时，如果该地区在送端，则联络线的传输功率极限将提高；反之，若该地区在收端，则联络线的传输功率极限将降低。但是当美国西部电网WSCC(western systems coordinating council)动态数据库不能重现1996年8月10日大系统事故时，研究人员最后修改了功率送出端(加拿大侧)的负荷模型，即从原来的恒电流模型改为恒功率模型，才仿真得到与实测比较接近的振荡曲线[7]。文献[7]从PSS输入信号及输出相位、幅值大小研究负荷模型对电力动态系统稳定的影响，通过分析表明由于PSS的影响导致原来认为保守的负荷模型变得乐观了。

本文采用静负荷特性分析送端负荷模型与自动电压调节器AVR(automatic voltage regulation)及电力系统稳定器PSS(power system stabilizer)的相互作用对电力系统动态稳定的影响。研究基于特征值分析的方法，计算程序采用中国电力科学研究院的PSD-BPA4.0版程序。

1 负荷静特性对电力系统稳定影响的原理

图1所示为单机无穷大系统。

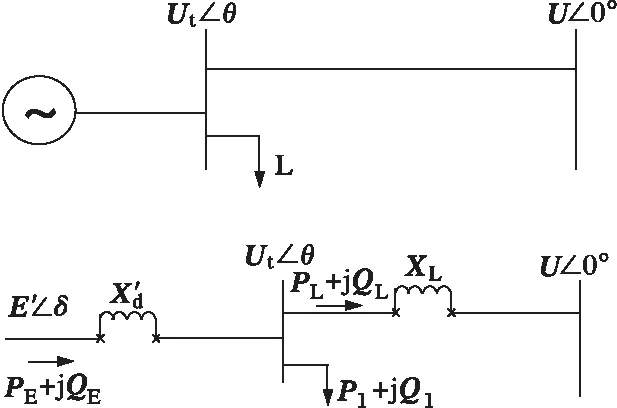
图1 单机无穷大系统

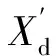
(1)

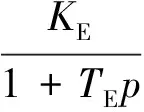
拉普拉斯算子。当负荷接在送端时，PE=P1+PL。送端的负荷模型分别采用恒功率、恒电流以及恒阻抗模型。

静态负荷模型为

(2)

P0、Q0分别为稳态运行时系统的负荷的有功与无功，np=nq=0，表示恒功率模型；np=nq=1，表示恒电流模型；np=nq=2，表示恒阻抗模型。

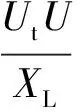
(3)

将式(2)代入式(3)，线性化可得

ΔPE=K1ΔUt+K2Δδ

(4)

设Δδ-Δθ=KΔδ，则有

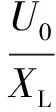
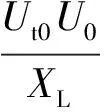
式中Ut0、U0、δ0、θ0为系统稳态运行时的量。

设

Ut=Ud+jUq

(5)

因为

(6)

而

(7)

因为

ΔId=ΔIL,d+ΔILoad,d

(8)

(9)

推导得

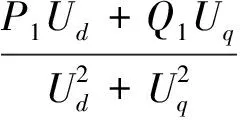
(10)

(11)

将式(9)和式(10)代入式(7)得

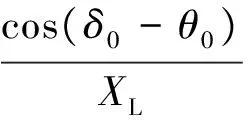
(12)

将式(11)与式(6)代入式(5)得

(13)

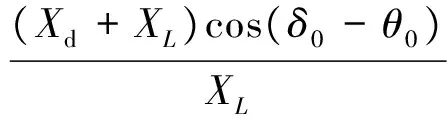
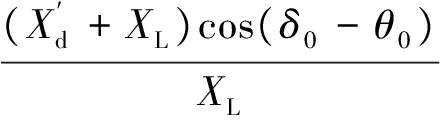
由上面可见，K2、K4与K6的值与负荷模型没有关系，但K1、K3与K5的值与负荷模型有关系。

1.1负荷模型与AVR相互作用对动态稳定影响

AVR对电力系统转矩的影响为

(14)

因为ΔPE≈ΔTE[7]，则有

(15)

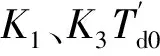
由上面的分析可以看出，当送端机组仅装AVR时，恒功率的负荷模型的阻尼转矩最大，恒电流次之，恒阻抗最差。

1.2负荷模型与PSS相互作用对动态稳定影响

当励磁系统加装PSS后，假设PSS的传递函数为Gpss(p)，输入信号选用Δω，因为

(16)

推导得到由PSS增加的系统的转矩为

ΔTE=

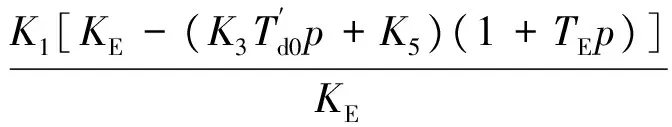
(17)

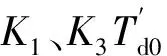
从上面的分析可以看出，当励磁系统加装PSS后，若PSS的参数设计合理，由PSS而增加的系统的阻尼转矩恒阻抗最大，恒电流次之，恒功率最差。

2 算例分析

系统的单线图如图2所示，该系统有两个对称的区域组成，每个区域有两台容量为600 MW的同步发电机。区域1与区域2的负荷分别为980 MW和1350 MW，区域1向区域2送电210 MW。

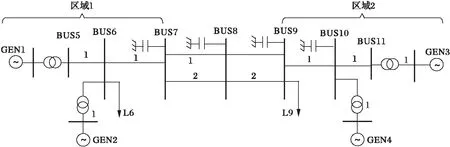
图2 两区域四机系统图

系统条件如下：

(1)发电机模型，本次研究采用考虑次暂态过程的、变化的详细模型；

(2)励磁系统模型，采用自并励励磁系统模型；

(3)PSS模型，采用PSS-2A模型。

通过小扰动程序计算发现，送端负荷模型的变化对区域间的振荡模式的影响比较大，对区域内振荡模式的影响较小。其主要原因是，区域间的电气距离较大，即XL的值较大，由前一章计算的各个系数的结果可以看出，此时负荷模型的变化对K1、K3与K5的值影响较大；而区域内的振荡XL值较小，此时负荷模型的变化对K1、K3与K5的值影响较小。为了节省篇幅，计算结果仅列出区域间的振荡模式。

表1 送端发电机无励磁系统振荡模式

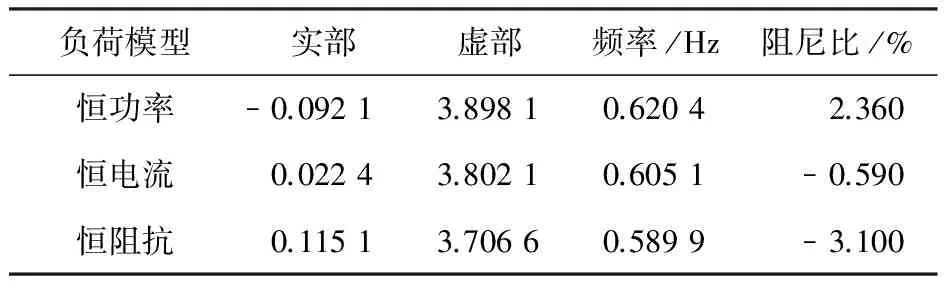
表2 送端发电机安装AVR振荡模式

表1～表3分别给出了送端机组无励磁系统，送端机组安装AVR及励磁系统加装PSS时系统的振荡模式，在此计算过程中受端机组一直装有励磁系统并加装PSS。

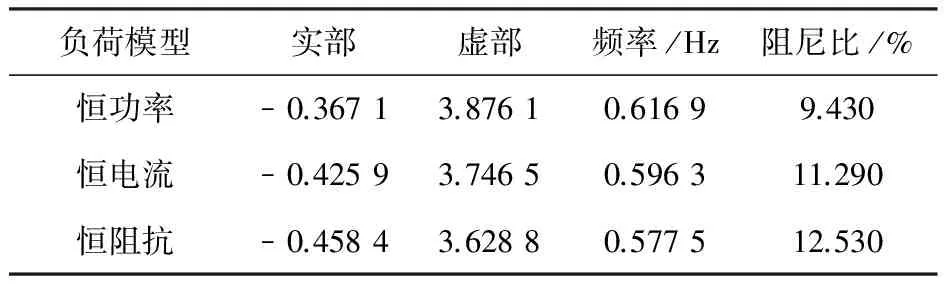
表3 送端发电机励磁系统加装PSS系统振荡模式

从表1～表3的结果可以看出，送端机组不安装励磁系统时，送端采用恒阻抗负荷模型最有利于系统动态稳定，恒电流次之，恒功率最差；送端发电机安装AVR后，系统的阻尼减弱，此时送端采用恒功率负荷模型最有利于系统动态稳定，恒电流次之，恒阻抗最差；若送端机组的励磁系统加装PSS后，系统的阻尼后增强，此时送端采用恒阻抗负荷模型最有利于系统动态稳定，恒电流次之，恒功率最差。此结果与上章的推理吻合。

3 结论

(1)当送端机组安装快速励磁系统时，自动电压调节器(AVR)无论送端采用何种静态负荷模型，系统的阻尼都会降低，但是采用恒功率模型时，系统阻尼降低的最少，恒电流次之，恒阻抗最多，此时送端采用恒功率模型更有利于电力系统的稳定。

(2)当送端机组的励磁系统加装PSS后，无论送端采用何种静态负荷模型，系统的阻尼都会加强，而采用恒阻抗的负荷模型时，系统的阻尼增加的最多，恒电流次之，恒功率最差，此时送端采用恒阻抗模型更有利于系统的稳定。

[1] Concordia C, Ihara S. Load representation in power system stability[J].IEEE Trans on Power Apparatus and Systems, 1982, 101(4): 969-977.

[2] Price W W, Taylor C W, Price W W,etal.Standard load models for power flow and dynamic performance simulation[J].IEEE Trans on Power Systems, 1995, 10(3): 1302-1313.

[3] 鞠 平，马大强.电力系统负荷建模[M].北京:水利电力出版社, 1992.

[4] 林舜江,李欣然,刘杨华(Lin Shunjiang, Li Xinran, Liu Yanghua).电力系统电压稳定性及负荷对其影响研究现状(Present investigation of voltage stability and composite load's influence on it)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(1): 66-74.

[5] 刘正谊,谈顺涛,苏盛,等(Liu Zhengyi, Tan Shuntao, Su Sheng,etal).电力系统综合负荷建模的实用化研究(Application of electric power aggregate load modeling for power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(2):43-47,62.

[6] 周文,贺仁睦,章健,等(Zhou Wen,He Renmu,Zhang Jian,etal).电力负荷建模问题研究综述(Review of electric load modeling research)[J].现代电力(Modern Electric Power),1999,16(2):83-89.

[7] Kosterev D N，Taylor C W，Mittelstadt William A. Model validation for the August 10,1996 WSCC system outage[J].IEEE Trans on Power Systems，1999，14(3):967-974.

[8] 李颖，贺仁睦(Li Ying, He Renmu).负荷与PSS的相互作用对系统动态稳定的影响(Effect of the interaction between load and PSS on power system dynamic stability)[J].电力系统自动化(Automation of Electric Power Systems),2004,8(28): 40-44.

[9] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.

EffectsofLoadModelonDynamicStabilityinPowerSystem

ZOU De-xu1， HE Ren-mu2， SI Da-jun3

(1.North China Electric Power University & Yun Nan Power Grid Graduate Workstation, Kunming 650217, China; 2.School of Electrical & Electronic Engineering,North China Electric Power University, Beijing 100085, China; 3.Yunnan Electric Power Test & Research Institute Group Company Limited, Kunming 650217, China)

This paper researches on effects of load model on dynamic stability in power system. Through constructing single-machine-infinite-bus system, interactions among different load models, automatic voltage regulator (AVR) and power system stabilizer(PSS) on dynamic stability of the power system are analyzed with sending-end loads using models of constant power, constant current and constant impedance. A typical two-area-four-machine system is used as the case study by using small perturbations program of PSD-BPA4.0. The results show that when the power system installs AVR, the sending-end loads with constant power model are helpful to the stability of the system, and when the system installs PSS, the sending-end loads with constant impedance model are helpful to the stability of system.

load model； dynamic stability； automatic voltage regulation(AVR)； power system stabilizer(PSS)

2009-09-25

2009-10-19

TM7

A

1003-8930(2011)01-0118-05

邹德旭(1984-)，男，硕士研究生，研究方向为电力系统动态稳定分析及控制。Email:zdxdb@126.com 贺仁睦(1944-)，女，教授，博士生导师，研究方向为动态电力系统分析控制和负荷建模。Email:xiaomin@public3.bta.net.cn 司大军(1976-)，男，博士，主要从事电力系统的运行分析、控制与研究工作。Email:dajunsi1976@163.com