基于网络结构和参数的临界割集的识别①
2011-10-30孟祥侠张有东李祥忠潘广林
孟祥侠, 张有东, 李祥忠, 潘广林
(1.华北科技学院机电工程系, 北京 101601; 2.吉林石油集团有限责任公司热电厂, 松原 138000)
基于网络结构和参数的临界割集的识别①
孟祥侠1, 张有东1, 李祥忠2, 潘广林2
(1.华北科技学院机电工程系, 北京 101601; 2.吉林石油集团有限责任公司热电厂, 松原 138000)
准确识别临界割集能为监测、控制系统在网络中合理布点提供关键的依据。该文基于网络拓扑结构和参数,利用耦合加权的思想形成网络中割集权系数,根据割集权系数的大小即可识别网络中最易导致系统失稳的“瓶颈”环节,并从稳定的角度揭示了输电网络本身固有的分区分层的结构特点对系统暂态稳定的影响。研究结果表明:网络拓扑结构和参数对系统的稳定性起支配的作用。对New England 10机系统进行仿真分析,验证了所提方法的有效性。
耦合; 加权; 割集权系数; 临界割集; 暂态稳定
近年来,由于电力系统跨区输电、跨区联网的形成,电网结构愈加复杂化,动态稳定问题日益突出[1,2]。因此,准确地识别出制约系统暂态稳定的“瓶颈”环节,以采取有效的监测、控制措施来提高系统的稳定性,是许多研究者关注的一个热点。
从网络入手研究电力系统的暂态稳定性问题最早始于20世纪80年代初,Bergen和Hill在文献[3]中,利用网络元件的联接强弱定义了割集的脆弱性指标,此文虽然计及了网络元件对暂态稳定的影响,但对输电网络本身固有的分区分层的结构特点没有深入的认识。文献[4]进一步从网络结构出发,揭示网络结构与系统稳定性的关系。文献[5]利用状态变量的耦合强弱对电力系统进行了动态分割,并指出网络的动态分割主要决定于网络的拓扑结构和参数,此方法的提出有助于深入理解网络结构本身固有的分区分层的结构特点,但未能从割集整体揭示网络结构脆弱性与系统暂态稳定性的关系。文献[6~10]利用支路势能法,通过分析故障后支路势能在网络中的分布与变化特点识别网络中的危险“断面”,确定临界割集,但此方法必须依赖全系统的仿真计算。
在此基础上,本文进一步利用耦合加权的思想形成网络中割集权系数,根据割集权系数的大小即可识别出网络中最易导致系统失稳的“瓶颈”环节,并从稳定的角度揭示了输电网络本身固有的分区分层的结构特点对系统暂态稳定的影响。
1 导纳阵耦合的思想
1.1 耦合思想
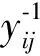

(1)
方向为由j指向i,其中Δ是Y阵的行列式,Δji是Δ去掉j行i列的子行列式;边权yji方向为由i指向j,其一阶循环积
(2)
可用来衡量节点i和j的耦合程度,并对应矩阵G的j行i列。

图1 相互耦合的两节点
一阶循环积gji的耦合程度,可从行列式的角度对其进行解释,n阶行列式Y阵按第j行展开为
Δ=yj1(-1)j+1Δj1+…+yjn(-1)j+nΔjn=
(gj1+…+gjn)Δ
(3)
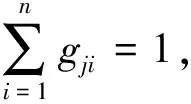
导纳阵Y及其逆阵Y-1分别为
(4)
(5)
因此可以将行矢量
i=1,2,…,n
(6)
对应矩阵G的第i行,将G阵记为
G=Y⊙Y-1
(7)
并定义G阵为导纳阵Y的耦合矩阵。
1.2 用导纳阵Y形成耦合阵G的步骤
为保证划分后的子系统内的各台发电机之间有直接的电气联系,或者说能保证按区域划分的原则,首先应将系统中的发电机节点重新编号,新编号的节点顺序应尽量使各台发电机在地理位置上互相邻接。具体步骤如下。
步骤1将系统中所有负荷节点的功率转换为导纳
(8)
使负荷节点转变为非注入节点。

Y0=AYbAT
(9)
形成节点导纳矩阵Y0。
步骤3消去Y0阵的非注入节点,只保留发电机节点,所获得的纳阵记为Y。
步骤4求阻抗矩阵Z=Y-1,进而求出
G=Y⊙Z
(10)
2 利用耦合值加权形成割集权系数
2.1 加权思想
G阵的每一个元都对应一个数值,该数值称为此元对应边的权。以下从割集的角度来分析,对于一个具有n个节点的系统,不失一般性,不妨选取这样一个割集,此割集将系统分为m和n-m个节点组成的子系统a和b。
定义1子系统a中的任一节点i(i=1,2,…,m)对子系统b的分配权是指子系统b中诸节点和节点i之间的权之和,即
(11)
而子系统a和b所对应割集的权系数为
(12)
图2给出了节点分配权以及割集权系数的几何解释。其中:αib为节点i与子系统b中诸节点的
权之和,用来衡量节点i和子系统b的耦合程度;αab为a中诸节点与子系统b的节点分配权之和,可用来衡量子系统a和b的耦合强弱,αab值小则子系统a和b耦合弱,αab值大则a和b耦合强。

图2 节点分配权αib及割集权系数αab
在对应的矩阵
G=
中,αab则为矩阵G的非对角子块Gab中所有元素的和。
2.2 利用加权形成割集权系数
由于重新编号的节点顺序在地理位置上尽可能互相邻接,因此可以按新编号的节点顺序,对系统中各相邻节点进行优化组合,图3给出了重新编号的节点顺序。节点1的组合为(1),(1,2),(1,3),(1,4),(1,2,3),(1,2,4),(1,2,5),…,但不会出现类似(1,6)或(1,2,7)这种在地理位置上不相邻的组合;节点2的组合为(2),(2,3),(2,5),(2,6),(2,3,6),(2,5,6),…,同样也不会出现类似(2,7)或(2,3,8)这种组合,以此类推。

图3 新编号的节点顺序
(14)
修正为
(15)

图4 割集权系数算法实现框图
值得一提的是,对于节点相邻但编号无法相邻的情况,图3中的节点1与3位置相邻,但编号不相邻。处理此种情况可以通过对耦合阵G中gij进行搜索,判断其是否为零,因为G阵同Y阵一样为稀疏矩阵,当j>i+1且gij≠0时,说明节点i与j在位置上邻接,此时可以将矩阵G中节点j处理成节点i+1。
3 利用割集权系数识别网络中临界割集
3.1 临界割集的概念
若在系统中的任一位置发生故障,使得系统失去稳定,系统失稳可能呈现为两群或多群振荡,不管是两群还是多群,其群间联络线通常都不是由一个割集组成,而是对应多个割集,但其中只有一个割集被“撕裂”,也即此割集包含的所有支路两端相角差均超过180°,此割集称为“临界割集”。图5示意地给出了机群A与机群B之间的临界割集。

图5 机群A与机群B的临界割集
3.2 利用割集权系数识别网络中临界割集
由于gij可用来衡量节点i与j的耦合程度,而
αab又是gij的函数,因此割集权系数αab可用来衡量子系统a和b之间的耦合强弱,利用其值的大小即可识别网络中的脆弱环节。
由于从稳定分析的观点,主要对系统中各台发电机的转子角δi随时间变化的函数感兴趣,因此使用只保留发电机内节点的割集权系数分析系统稳定性是合理的,它虽然掩盖了网络的拓扑性质,但从宏观上可快速地识别出制约系统暂态稳定的“瓶颈”环节。
然后在“瓶颈”环节处结合系统失稳时群间联络线各支路相角差的变化特点,即可准确识别出网络中“临界割集”。
4 算例与仿真分析
以New England 10机系统为算例,表1给出了10机系统部分割集权系数的大小。时域仿真采用中国电科院研制的综合程序(PSASP)。在给定的潮流方式下,#30发电机出口发生三相瞬时性故障,切除时间为0.31 s时,系统呈现为{39}、{30,31,32,33,34,35,36,37,38}两群失稳,其部分支路两端相角差变化曲线如图6所示,其中,支路1-2、8-9两端相角差超过180°而趋于无界,而所有其他支路两端相角差均在有界范围内变化,因此,由支路1-2、8-9构成的割集为临界割集。为了不失一般性,表2给出了不同故障位置系统呈现出的失稳模式,图7为对应的临界割集。

表1 10机系统部分割集权系数

表2 10机系统不同故障位置的失稳模式
由表2可以看出, 尽管大部分的故障并未发生在支路1-2、8-9或26-28、26-29构成的临界割集或其附近的割集上,但都导致系统在此两个割集处“撕裂”。
之所以在网络中有“系统在此处发生故障,而在彼处的割集被撕裂”,并导致系统失稳的现象产生,在一定程度上是受网络结构和参数的制约。由表1割集权系数的大小可以看出,在机群{39}与{30,31,32,33,34,35,36,37,38}之间割集权系数最小,为0.022 323;机群{38}与{30,31,32,33,34,35,36,37,39}之间割集权系数次之,为0.035 485,说明{39}与其剩余机群、{38}与其剩余机群之间联系相对较弱,此两个部位为网络上相对脆弱的环节。
而位于脆弱环节中的割集{1-2、8-9}和{26-28、26-29}在结构上又分别处在{39}与其剩余机群、{38}与其剩余机群之间联络线的中部,容易成为振荡中心所落之部位,因而在系统受到扰动后,最易在此两个环节失稳。
当然,系统的暂态稳定性不仅仅取决于网络拓扑结构和参数,还与故障位置、发电机的转动惯量以及初始潮流等多种因素有关,但网络拓扑结构和参数对系统的暂态稳定性起支配的作用。
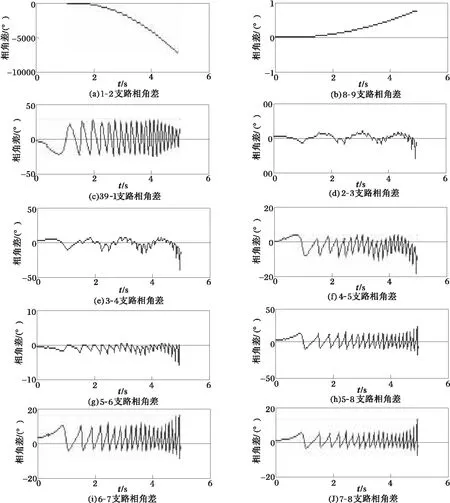
图6 #39机与系统失稳时部分支路两端相角差变化
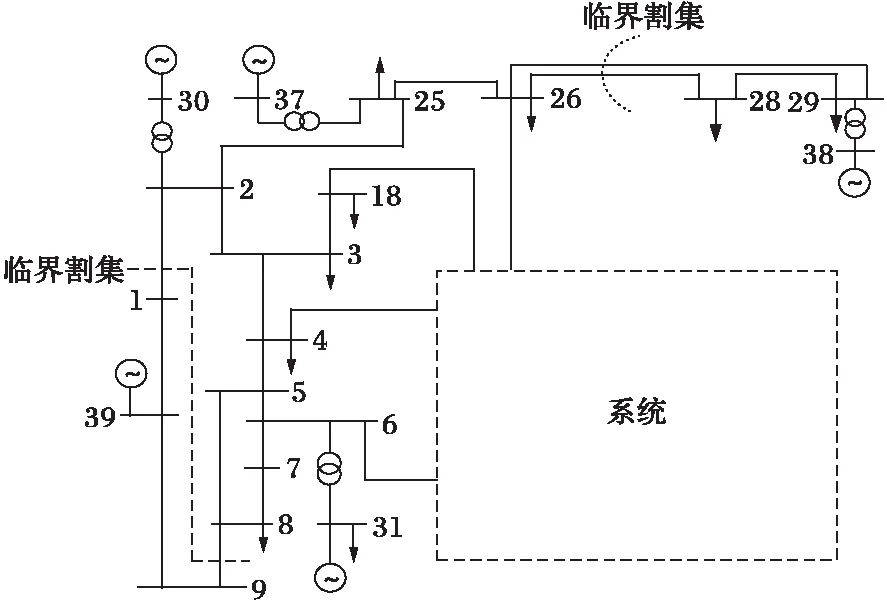
图7 10机系统的临界割集
5 结语
本文基于输电网络本身固有的分区分层的结构特点,利用耦合加权的思想形成网络中割集权系数,根据割集权系数的大小即可识别出网络中最易导致系统失稳的脆弱环节。此方法不依赖于数值仿真计算,方法简单,计算量小,且可从网络整体观察问题,有助于解决大规模互联电力系统长期制约暂态稳定的“瓶颈”问题,为监测、控制系统在网络中的合理布点提供了一定的依据。
[1] 赵遵廉(Zhao Zunlian).中国电网的发展与展望(Development and prospect of power system in China)[J].中国电力(Electric Power), 2004,37(1):1-6.
[2] 薛禹盛(Xue Yusheng). 综合防御由偶然故障演化为电力灾难——北美“8·14”大停电的警示(The way from a simple contingency to system-wide disaster-lessons from the Eastern Interconnection Blackout in 2003)[J].电力系统自动化(Automation of Electric Power Systems), 2003, 27(18):1-5,37.
[3] Bergen A R, Hill D J. A structure preserving model for power system stability analysis[J].IEEE Trans on Power Apparatus and Systems,1981, 100(1):25-35.
[4] 赵金利,张群华,余贻鑫,等(Zhao Jinli, Zhang Qunhua, Yu Yixin,etal).输电网网架结构的谱聚类分析算法(Spectral clustering approach for structure analysis of transmission networks)[J].电力系统及其
自动化学报(Proceedings of the CSU-EPSA), 2009, 21(4):8-11,75.
[5] 王雨蓬, 马昭彦(Wang Yupeng, Ma Zhaoyan).电力系统的动态分割(Dynamic partition of power system)[J].中国电机工程学报(Proceedings of the CSEE), 2001, 21(12): 45-49.
[6] 穆钢,蔡国伟,胡哲,等(Mu Gang, Cai Guowei, Hu Zhe,etal).机网结合的暂态稳定评价方法——关键割集组法(Network-machine combined transient stability assessment method——key cutsets method)[J].清华大学学报:自然科学版(Journal of Tsinghua University:Science and Technology),1997,37(7):97-101.
[7] 蔡国伟,穆钢,程浩忠,等(Cai Guowei, Mu Gang, Cheng Haozhong,etal).基于支路暂态势能和两端电压识别临界机群的新方法(Approach to identify the critical cluster of machines based on line transient potential energy and voltage)[J].中国电力(Electric Power),2002,35(5):40-44.
[8] 蔡国伟,穆钢, Chan K W,等(Cai Guowei, Mu Gang, Chan K W,etal).基于网络信息的暂态稳定性定量分析——支路势能法(Branch potential energy method for power system transient stability assessment based on network dynamic variables)[J].中国电机工程学报(Proceedings of the CSEE),2004,24(5):1-6.
[9] Cai G W, Chan K W, Cheng H Z,etal.Transient instability detection using line transient potential energy[J].Electric Power Components and Systems, 2004, 32(6): 627-643.
[10]蔡国伟,孟祥侠,刘涛(Cai Guowei, Meng Xiangxia, Liu Tao).电力系统振荡中心的暂态能量解析(Study on transient energy around power system oscillation center)[J].电网技术(Power System Technology),2005,29(8):30-34.
IdentificationofCriticalCut-setBasedonNetworkStructureandParameter
MENG Xiang-xia1, ZHANG You-dong1, LI Xiang-zhong2, PAN Guang-lin2
(1.Mechanical and Electrical Engineering Department, North China Institute of Science and Technology, Beijing 101601, China; 2.Thermal Power Plant of Jilin Petroleum Group Corporation, Songyuan 138000, China)
Accurately identifying critical cut-set can provide very important basis for monitor/control system allocation in network.Based on network topological structure and parameter,cut-set weighted coefficient in network is formed by means of coupling and weighted thinking,"bottleneck"section which is most liable to make system losing stability in network is identified according to magnitude of cut-set weighted coefficient,the law which the transmission network itself inherntly hierarchical sturcture characteristics affect the transient stability of power system is revealed in terms of stability.The results show that topological structure and parameter of network dominate stability of power system.Simulation results and analysis on New England 10 machines system testify the validation of the proposed method.
coupling; weighted; cut-set weighted coefficient; critical cut-set; transient stability
2010-07-29
2010-09-17
TM711
A
1003-8930(2011)01-0074-06
孟祥侠(1973-),女,硕士,讲师,主要从事电力系统稳定与控制方面的教学和科研工作。Email:mengxiangxia@ ncist.edu.cn 张有东(1970-),男,副教授,主要从事电力系统控制方面的教学和科研工作。Email:youdongzhang@ncist.edu.cn 李祥忠(1969-),男,工程师,主要从事发电厂电气分厂技术与管理工作。Email:lxz660297@163.com
