风电场风速概率分布参数计算新方法①
2011-10-30陈国初张延迟徐余法
陈国初, 杨 维, 张延迟, 徐余法
(上海电机学院电气学院, 上海 200240)
风电场风速概率分布参数计算新方法①
陈国初, 杨 维, 张延迟, 徐余法
(上海电机学院电气学院, 上海 200240)
风能资源评估关系到风电的经济性和开发价值,一个地区的风速概率分布是该地区风能资源状况的最重要指标之一。在认为风电场风速服从双参数韦布尔(Weibull)分布前提下,为了提高参数计算精度,从智能化的角度提出尝试采用改进的微粒群算法对Weibull双参数进行建模和优化。由此参数估算能直接反映出风能资源特性的风能特征指标,与由常规最小二乘法、丹麦WAsP软件以及历史风速数据序列所计算的结果相比,实验表明该方法拟合精度更高,更接近实际风速状况,为风电场规划设计提供了更具价值的参考。
风电场; 风速概率分布; 韦布尔分布; 改进微粒群算法
风能是一种可再生的无污染绿色能源,风力发电随着人们对能源和环境问题的关注而得到迅速发展[1]。20世纪70年代未,风电场的概念首先由美国提出,经过30年的发展,截止到2009年底,我国风电新增装机容量1 380.3万kW,累计装机容量达到2 580万kW,超过德国,位列全球第二,主要分布在三北地区和东南沿海。
由于风速概率分布模型直接关系到风电的经济性和开发价值,所以风速概率分布模型的研究是风电场建模中一个非常重要的课题[2]。一个地区的风电场风速概率分布是该地区风能资源统计特性的重要指标。由于气候地理因素的复杂性形成各地风速分布多变的事实,目前还没有从成因上和理论上给出某地风速概率分布的形式。为了较精确地描述风速的随机性和间歇性及其变化特性,所以对风况只能进行长期观测,进行统计分析,才能掌握风速分布及其变化规律,在此基础上建立数学统计模型表示实际风速分布。目前有不少研究对风速分布采用各种统计模型来拟合,如:瑞利(Rayleigh)分布[3]、β分布[4]、韦布尔(Weibull)分布[5,6]等,但是应用最多的还是两参数Weibull分布模型。
对于Weibull模型,只要确定了形状参数k和尺度参数c之后,体现风资源特性的最重要两个指标,年平均风速、年平均风能密度都可以求得,所以k和c的精度直接影响特性指标的精度。在具体使用过程中,参数的确定应根据当地可供使用的风速统计资料的不同情况做出不同的选择。通常可采用的统计方法有最小二乘法LSM(least squares method)[7]、极大似然估计法[8]、矩估计法[9]等。
其中,LSM计算方便、简单、易于实现,较为常见,但其计算精度不高;矩估计法的优点在于它的简单性,缺点是不能完全利用样本的信息;极大似然法估计虽具有渐近无偏性、一致性、渐进有效性,但是它的两个方程均为超越方程,且相当复杂,需利用迭代法经编程求解,此外,当k值较小时,迭代不易收敛甚至无解。因此,它难以作为一个易行、普适的方法予以应用。可见这些传统方法有的简单易实现,但精度差,有的精度高,但难以实现,因而迫切需要探索出更为有效的计算方法。为此,本文在认为风速服从两参数Weibull分布模型的前提下,从智能化的角度提出采用改进的微粒群算法,并结合实际的风电场现场数据,用于Weibull双参数的建模与寻优。
1 风速概率分布模型
实际风速是连续分布的,一般可采用被认为是一种形式简单且能较好地拟合实际风速概率分布模型的双参数Weibull分布。设由测风仪获得某风电场的风速序列(V1,V2,…,Vn)服从两参数Weibull分布,则分布函数为

(1)
其概率密度函数为
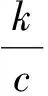
(2)
式中:c和k分别为Weibull分布的尺度参数和形状参数,这两个参数控制Weibull分布曲线的形状。尺度参数c反映该风电场的平均风速,其量纲与速度相同;k表示分布曲线的峰值情况,无量纲。
2 风资源主要特征指标
1)平均风速
风速是单位时间内空气在一定方向上所移动的距离,原始风速数据必须经过一定时期的观测才能得到。一般采用每小时平均风速值,它是描述风能资源状况、进行风能资源评估的基本参数和必备数据,单位为m/s。
根据历史风速数据计算平均风速的公式为
(3)
亦可根据Weibull分布参数k和c,近似估算平均风速
(4)
2)平均风能密度
平均风能密度是一定时间段内风能密度的平均值,它是描述一个地方风能潜力的最方便最有价值的量,单位为W/m2。风能密度和空气密度有直接关系,一般来说,空气密度大,风能密度也就高。
根据历史风速数据,计算平均风能密度的公式为
(5)
亦可根据Weibull分布参数k和c,近似估算平均风能密度为
(6)
式(6)中,各量意义同前,ρ为年平均空气密度,本文取1.092 2 kg/m3。
3 Weibull参数计算方法
虽然最小二乘法法在实际工程中应用甚为广泛,但其原理相对简单,因此其计算过程本文不做介绍,仅就改进微粒群算法的具体建模和寻优过程进行详细介绍。
3.1 改进的微粒群算法
3.1.1 基本微粒群算法
微粒群算法PSO(particle swarm optimization algorithm)是Kennedy和Eberhart[11]于1995年提出的一种新的进化计算算法,其核心思想来源于群体中个体之间信息的社会共享和协同进化。PSO具有参数少、结构简单、高效、收敛快等优点,使得它在解决大量的高维、多峰、非线性等问题中得到广泛的应用,并取得较好的效果[12~14]。其原理如下:假设有m个微粒组成的一微粒群在D维搜索空间中,每个个体都是优化问题的一个潜在解,其中第i个微粒的空间位置为xi=(xi1,xi2,xi3,…,xiD),其中i=1,2,…,m,将它代入优化目标函数可以计算出相应的适应值,根据适应值可衡量xi的优劣,第i个微粒所经历的最好位置称为其个体历史最好位置,记为Pi=(pi1,pi2,pi3,…,piD),对应的为个体历史最好适应值为Pbest,具有各自的飞行速度Vi=(vi1,vi2,vi3,…,viD)。所有微粒经历过的位置中的最好位置称为全局历史最好位置,记为Pg=(pg1,pg2,pg3,…,pgD),相应的适应值为全局历史最好适应值Fg。对第k代的第i个微粒,其第d维速度、位置(1≤d≤D)迭代方程为
(7)
(8)
式中:ω为当前惯性权值,本文约定ω=ωmax-iter(ωmax-ωmin)/MaxIt,iter为当前迭代次数,ωmax、ωmin为ω的上下限,MaxIt为最大允许迭代次数;c1和c2都为正常数,称为学习因子;r1和r2是两个在[0,1]范围内变化的随机数,通常这种惯性权值递减的PSO称为基本PSO。
3.1.2 简化的微粒群算法
通过分析基本粒子群算法的进化迭代方程式(7)和式(8)可以发现:在粒子群算法中,粒子速度的概念不是必需的。根据基本PSO的两个迭代方程来看,微粒群最终的目的是要粒子的位置向量x去逼近解空间的最优解,因此,微粒在整个搜索过程中,其轨迹变化的最本质的体现是其位置向量x的变化过程,所以可以直接考察x的变化轨迹;另外,基本PSO模型中的速度不是常说的物理意义上的速度,即位移对时间的一阶导数,而仅仅只有数学上的意义,其方向表示微粒的下一步的迭代方向,其大小表示微粒的下一步的迭代步长,但这个方向有可能偏离微粒的正确的进化方向,从而造成微粒难以收敛的现象;由以上分析可知,微粒进化方程的速度项完全可以去掉。综上,式(7)和式(8)两个方程可以合并为一个单一的进化方程,其方程为
(9)
由位置迭代公式可以看出:在去掉速度项的基本PSO中,第一部分是“惯性”部分,表示粒子对上一次迭代速度的继承;第二部分为“认知部分”,是粒子对自身的思考;第三部分为“社会部分”,表示粒子间的信息共享和相互合作。当c1≠0且c2=0时,对应“认知模型”;当c1=0且c2≠0时,对应“社会模型”;当c1≠0且c2≠0时,对应“完全模型”。可见,与基本PSO相比,简化的基本PSO不仅迭代原理没有发生任何变化,而且其结构更加简单。
3.1.3 对微粒进行分类
在微粒群的进化过程中,有必要根据各个微粒适应值的差异将其进行合理的分类,这样能有效保证不同微粒对全局搜索和局部搜索的需求能力差异的平衡。为此,可以根据微粒适应值的均值度量来把微粒划分为三类。这里以极小化为例,在第k代进化中,求出所有微粒的均值aver,最好适应值fmin,最差适应值fmax,分别把具有这两种适应值的微粒称为最好微粒和最差微粒,具体的进化模型方程如下所示。
1)较好微粒的进化模型
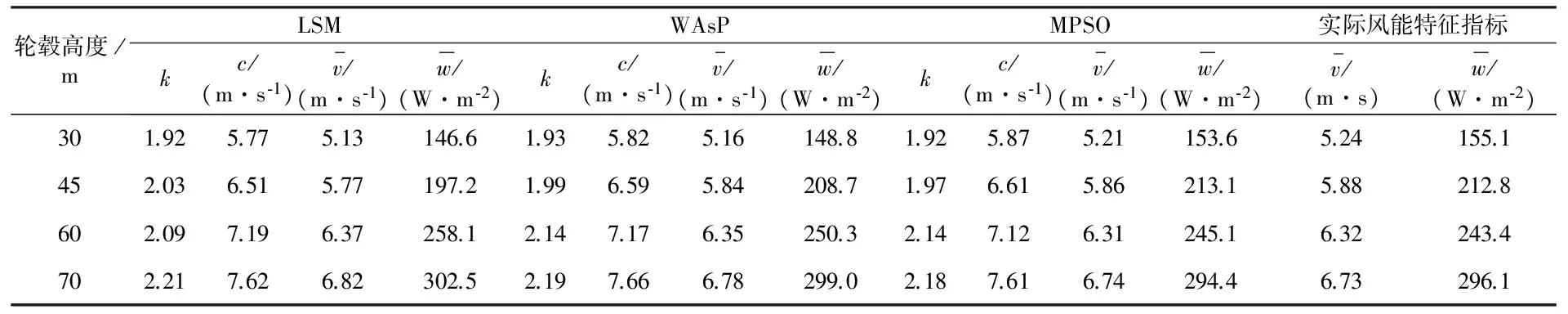
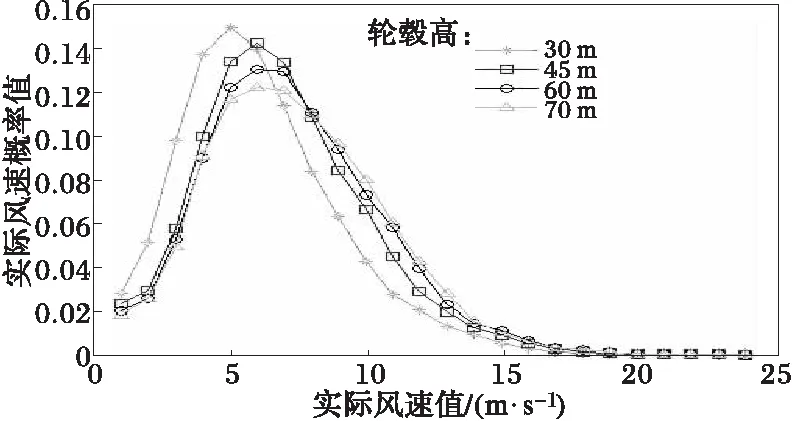
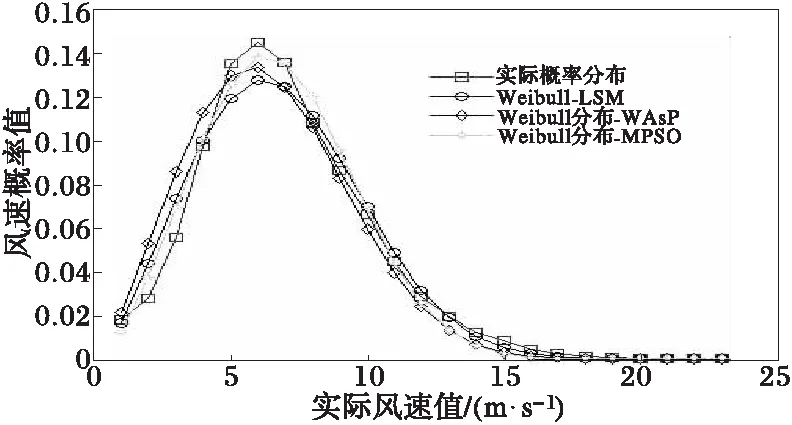
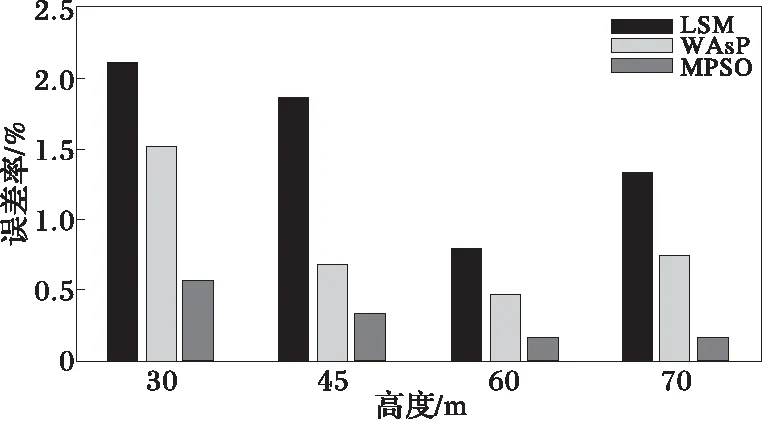
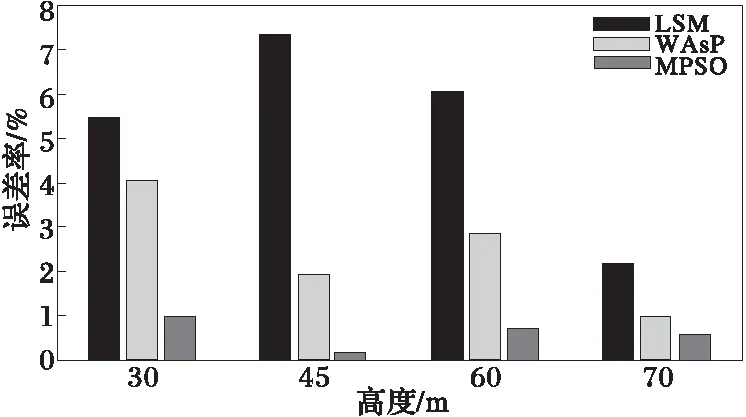
若微粒的适应度满足fmin≤f(i) (10) 式中,c=c1+c2。 2)普通微粒的进化模型 若微粒适应度满足aver1≤f(i) (11) 3)较差微粒的进化模型 若微粒适应度满足aver2≤f(i)≤fmax,则这部分微粒是群体中较差的个体,这些微粒距离全局最优值较远,应当采用完全模型进行调整,使这些微粒加快收敛速度靠近全局最优解,其位置进化方程为 (12) 在完全模型的进化过程中,在迭代初期,c1取较大值、c2取较小值有利于加强微粒的自我学习能力,在迭代后期,c1取较小值、c2取较大值有利于加强微粒间的信息共享和群体之间的学习能力,这样可以继承经典时变加速系数PSO的优秀部分。在认知模型和社会模型的进化过程中,为了加重认知模型的自身认知能力和社会模型的社会学习能力,把完全模型中的2个学习因子相加,即c=c1+c2。由于惯性权重ω有平衡全局探索和局部开发的能力,所以这三个进化模型ω均采用基本PSO中线性递减的方式。本文将上述改进的微粒群算法记为MPSO。 3.2Weibull双参数建模 综上,可建立风速Weibull分布参数的目标误差优化函数为 (13) 式中:E(k,c)为误差平方和函数,其极小值时对应的k和c,即为所要求的最优解(k,c);pvi为实际第i个风速值vi(也就是vi=im/s)的统计概率;fVi是将Vi代入式(2)中得到的韦布尔概率值,n为根据原始风速数据所分的风速段数。 下面实例是根据某风电公司提供的东北某风电场近一年的测风数据,从中分别选取30 m、45 m、60 m以及70 m高的测风塔2007年4月7日~2008年4月6日这一年的测风数据,这些数据是每隔10 min一个风速点。在这一年中,每个轮毂高度均有6×24×366=52 704个数据。本实验中,微粒的数目设为30,最大迭代代数设为1 000,ω从0.9线性递减到0.4,c1从2.05线性递减到0.50,c2从0.50线性递增到2.05,c=4.1,为了减少根据经验选择的ω和c1、c2之间的偶然冲突,本实验在每个不同轮毂高度所用的计算方法均进行100次独立测试取其均值,具体计算结果见表1以及图1~图4。 表1 不同轮毂高度的Weibull参数及风资源特征指标统计结果 图1 不同轮毂高度的实际概率分布 图2 45 m高的概率分布 丹麦WAsP软件附带的风机库汇集了70余种风力发电机组数据WTGS(wind turbine generator system),利用WAsP-Turbine Editor可调用WTGS特性参数,并可根据Weibull两参数估算风能特征指标。 从表1和图1可以看出,随着轮毂高度的增加,可以采用较大的风机叶片,从而获得较大的扫风面积,进而捕捉到更多的风能,这也就是新型的风力发电机组塔架越来越高,风轮直径越来越大的主要原因。 图2是选取的轮毂高度为45 m高的实际风速概率分布和Weibull分布对比图,从图可以直观看出,与LSM和WAsP所计算出来的参数所拟合的效果相比,MPSO算法拟合的结果更加接近实际的风速概率分布。 从表1以及图3和图4均可以清晰看出,用MPSO所寻优的Weibull参数所计算出的平均风速和平均风能密度的误差率均小于LSM和WAsP的计算结果,其计算值更加接近实际值,而且平均风速的最大误差率不到1%,平均风能密度的最大误差率不到1%,均符合实际工程要求,表明了该方法的合理性和有效性。 图3 不同轮毂高度的平均风速误差对比 图4 不同轮毂高度的平均风能密度误差对比 从表2中可以看出,相同轮毂高度、采用相同直径风机叶片所获得的风资源,用LSM所优化出的参数k和c所花销的时间成本明显小于其他两种方法,并且MPSO所用的计算时间仍然高于WAsP所得结果;但是,从实际工程精度要求的角度来看,MPSO所多花的这点时间开销成本是远远划算的。 表2 不同轮毂高度的各种方法计算时间 本文对微粒群算法的寻优机理进行研究,提出一种改进的微粒群算法,并尝试采用此改进的微粒群算法对Weibull参数进行寻优,用拟合出的双参数对两个重要的风资源特征指标进行计算。实验结果表明,与常规最小二乘法、丹麦WAsP软件以及利用实际的风速源数据进行计算的结果相比,该方法具有更好的拟合效果,所计算结果更具实际参考性。目前还没有从智能化的角度对Weibull双参数进行建模与优化的报道,本文提出的方法为风电场Weibull分布参数的建模和寻优进行了多元化的尝试,扩宽了该模型求解与应用的领域。 [1] 庄晓丹(Zhuang Xiaodan), Jiang J N.大型风电场的风能损失计算(Estimation of loss of wind energy in large-scale wind farm)[J].电力系统自动化(Automation of Electric Power Systems), 2009, 33(12): 85-90. [2] 陈树勇, 戴慧珠(Chen Shuyong, Dai Huizhu). 风电场的发电可靠性模型及其应用(Reliability model of wind power plants and its application)[J].中国电机工程学报(Proceedings of the CSEE), 2000, 20(3) : 26-29. [3] Gokcek M, Bayulken A, Bekdemir S.Investigation of wind characteristics and wind energy potential in Kirklareli, Turkey[J].Renewable Energy, 2007, 32 (10) :1739-1752. [4] Carta J A, Ramirez P, Velazquez S.Influence of the level of fit of a density probability function to wind-speed data on the WECS mean power output estimation[J].Energy Conversion and Management, 2008, 49 (10): 2647-2655. [5] Cellura M, Cirrincione G, Marvuglia A,etal.Wind speed spatial estimation for energy planning in Sicily: Introduction and statistical analysis[J].Renewable Energy, 2008, 33(6): 1237-1250. [6] 丁明, 吴义纯, 张立军(Ding Ming, Wu Yichun, Zhang Lijun). 风电场风速概率分布参数计算方法的研究(Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms)[J].中国电机工程学报(Proceedings of the CSEE), 2005, 25(10): 107-110. [7] Carta J A, Ramirez P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions[J].Renewable Energy, 2007, 32(3): 518-531. [8] Eskin N, Artar H, Tolun S. Wind energy potential of Gokceada Island in Turkey[J].Renewable and Sustainable Energy Reviews, 2008, 12(3): 839-851. [9] Shamilov A, Kantar Y M, Usta I.Use of MinMaxEnt distributions defined on basis of MaxEnt method in wind power study[J].Energy Conversion and Management,2008, 49(4): 660-677. [10]徐宝清, 田德, 吴骅, 等(Xu Baoqing, Tian De, Wu Hua,etal).风速Weibull分布参数确定方法研究(Methods for solving two-parameter wind velocity Weibull distribution)[J].农业工程学报(Journal of Agricultural Engineering),2007, 23(10): 31-34. [11]Eberhart R, Kennedy J. New optimizer using particle swarm theory[C]∥The International Symposium on Micro Machine and Human Science, Nagoya, Japan: 1995. [12]顾益磊, 王西田, 赵大伟, 等(Gu Yilei,Wang Xitian, Zhao Dawei,etal).基于改进粒子群算法的附加励磁阻尼控制器设计(Optimization design of supplementary excitation damping controller based on improved particle swarm optimization algorithm)[J].电力系统自动化(Automation of Electric Power Systems), 2009, 33(7): 11-16. [13]肖军, 刘天琪, 苏鹏(Xiao Jun, Liu Tianqi, Su Peng). 基于双种群粒子群算法的分时段电力系统无功优化(A time-interval based reactive power optimization algorithm using double-population particle swarm optimization)[J].电网技术(Power System Technology), 2009, 33(8): 72-77. [14]罗绮, 吕 林(Luo Qi, Lü Lin). 一种新的混合优化算法求解配电网重构(A new hybrid optimal algorithm to solve distribution network reconfiguration)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2009, 21(1): 89-92. [15]杨洪明,谭韬, 孟宪志(Yang Hongming, Tan tao, Meng Xianzhi). 电力市场古诺动态博弈的时滞反馈混沌控制(Time-delayed feedback chaos control of dynamic Cournot game in power market)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010, 22(1): 5-12. [16]吕林, 周学亿(Lü Lin,Zhou Xueyi). 改进PSO算法和Lagrange乘数法应用于短期发电计划(Improved PSO algorithm and Lagrange multipliers method application in the short-term scheduling)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010, 22(1): 106-110,125. NewComputationMethodofWindSpeedProbabilityDistributionParametersinWindFarm CHEN Guo-chu, YANG Wei, ZHANG Yan-chi, XU Yu-fa (School of Electric Engineering, Shanghai Dianji University, Shanghai 200240, China) Wind speed probability distribution in a region is one of the most important indicators of wind energy resources condition in an area,because wind resource assessment is related to wind power's economic and development value.In order to improve computation precision of parmeters,a new computation method was proposed based on intelligence point in this paper.This method is tried to use modified particle swarm optimization algorithm to optimize the two parmeters of Weibull distribution.Wind indicators reflecting the wind energy resource characteristics are calculated according to these two optimal parameters.Compared to the results of conventional least squares method,Denmark WAsP software and historical wind speed data sequences,the proposed method has higher fitting precision and closer to actual wind conditions.It provides a more valuable reference to plan and design of wind farm. wind farm; wind speed probability distribution; Weibull distribution; modified particle swarm optimization algorithm 2010-08-04 2010-11-01 上海市教委科研创新重点项目(09ZZ211);上海市教委重点学科(J51901);闵行区-上海电机学院区校合作项目(08Q07) TM81 A 1003-8930(2011)01-0046-06 陈国初(1971-),男,博士,副教授,研究方向为复杂系统的建模、仿真与智能算法及其应用研究。Email:chgcsh@yahoo.com.cn 杨 维(1984-),男,硕士研究生,研究方向为智能化方法及其风电场建模中的应用。Email:tomyangwei@163.com 张延迟(1967-),男,博士研究生,副教授,研究方向为大型风力发电机组电控系统、电力系统灵活交流输电装置、电力系统仿真。Email:zhangyc@sdju.edu.cn 徐余法(1964-),男,博士,教授,硕士生导师,研究方向为电机控制,人工智能,故障诊断,软测量技术,信息融合,随机集理论。Email:xuyf@sdju.edu.cn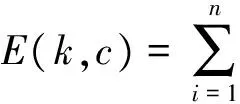
4 实例与结果分析

5 结语
