双模拟与模态逻辑

姚从军

(湖南科技学院思政部，湖南永州 425100)

双模拟与模态逻辑

姚从军

(湖南科技学院思政部，湖南永州 425100)

首先基于模型上的模拟概念定义了模型上的双模拟概念，并给出双模拟模态不变性和模态等价性的定义。在此基础上，讨论了模态逻辑与双模拟之间的关系;进一步分别在语言ML(τ，Φ)和ML∞(τ，Φ)中分析了模态等价性与双模拟不变性之间的关系;最后证明了正存在模态公式与双模拟之间的关系，并把正存在模态公式刻画为一阶公式双模拟不变部分。

模拟;双模拟;模态逻辑;正存在模态公式;双模拟不变性

一、基础知识

定义1.1 基本模态语言ML(◇，Φ)是由一个命题变项的集合Φ和一元模态算子◇组成的。其中Φ的元素通常被记作p，q，r等等。基本模态语言的合式公式φ由下面的规则给出

φ∷=p|⊥|﹁φ|φ∨ψ|◇φ，其中p∈Φ。

在BML中，如果将∨换为∨(允许无穷)得到无穷模态语言ML∞。

定义1.2 一个模态相似型是一个对τ=(0，ρ)，其中0是一个非空集，并且ρ是一个从0到N的函数，即ρ:0→N。0的元素被称为模态算子，我们用Δ，Δ1，Δ2，…表示0中的元素，函数ρ给每一个算子 Δ∈0指定一个自然数，表示 Δ的元数。

为了与定义1.1一致，我们把一元三角Δ1称作菱形，并且把它们记作或〈a〉，其中的a取自某个标号集。有时，我们假设算子的元数是已知的，因此，不区别τ和0。

定义1.3 一个模态语言ML(τ，Φ)是由一个模态相似型τ=(0，ρ)和一个命题变项的集合Φ构成的。τ和Φ上的模态公式的集合Form(τ，Φ)由下面的规则给出

φ∷=p|⊥|﹁φ|φ∨ψ|Δ(φ1，…，φρ(Δ)，其中p∈Φ。

同样，在ML(τ，Φ)中，如果将∨换为∨(允许无穷)得到无穷模态语言ML∞(τ，Φ)。

基本模态语言 ML(◇，Φ)是模态语言ML(τ，Φ)的一个特例，这里τ只包含一个一元模态词。

定义1.4 令τ是一个模态相似型，一个τ－模型是一个三元组M=(W，{RΔ|Δ∈τ}，V)。这里W是一个非空集;对τ中的每个n(n≥0)元模态词Δ，RΔ是W上的n+1元关系;V是赋值函数，其定义域为模态语言ML(τ，Φ)的命题变元集Φ，值域为P(W)。当τ={◇}时，则得到基本模态语言的模型M=(W，R，V)。

定义1.5 令τ是一个模态相似型，M=(W，{RΔ|Δ∈τ}，V)是一个τ－模型，如果对M的每一个状态w和每一个关系RΔ(Δ∈τ)，集合{(v1，…，vn)|RΔwv1…vn}是有穷的，则称M是像有穷的。

二、模型上的双模拟概念

先给出模型上的模拟定义:

定义2.1 令τ是一个模态相似型，令M=(W，{RΔ|Δ∈τ}，V)和M'=(W'，{RΔ'|Δ∈τ}，V')是两个τ－模型，如果Z⊆W×W'是一个满足下面的条件二元关系:对于任意的w∈W，w'∈W'，Δ∈τ，wZw'当且仅当

(i)对所有命题字母p，如果w∈V(p)，那么w'∈V'(p);

(ii)对于所有的v1，…，vn，如果RΔwv1…vn，那么存在v1'，…，vn'∈W'使得RΔ'w'v1'…vn'且对所有的i(1≤i≤n)，viZvi'。

则Z被称为从M到M'的一个模拟。

对于基本的模态语言而言，即τ是一个基本模态相似型，第二条就变为:

(ii)'对于所有的v∈W，如果Rwv，那么存在v'∈W'使得R'w'v'，并且vZv'［1］110。

如果从M到M'存在一个模拟关系Z，使得wZw'，那么我们说w'模拟w，或者说Z是w到w'的模拟关系，也可以记作w →w'。如果M=M'，我们称Z为M上的一个模拟。

定义2.2 令τ是一个模态相似性，M=(W，{RΔ|Δ∈τ}，V)和M'=(W'，{RΔ'|Δ∈τ}，V')是两个τ－模型。如果Z⊆W×W'是一个满足下面的条件的二元关系:对于任意的w∈W，w'∈W'，a∈A，如果wZw'当且仅当

(i)对所有命题字母p，w∈V(p)当且仅当w'∈V'(p);

(ii)存在LTS到LTS'一个模拟关系为Z1，使得对于所有的v1，…，vn(W，如果RΔwv1…vn，那么存在v1'，…，vn'∈W'使得RΔ'w'v1'…vn'，并且对所有的i(1≤i≤n)，viZ1vi';

(iii)存在LTS到LTS'一个关系为Z2，且满足是LTS'到LTS的模拟关系，使得对于所有的v1'，…，vn'∈W'，如果RΔ'w'v1'…vn'，那么存在v1，…，vn∈W使得RΔwv1…vn，并且对所有的i(1≤i≤n)，viZ2vi'。

则Z⊆W×W'被称为从M到M'的一个双模拟。

如果M的状态w和M'的状态w'是双模拟的，那么我们记作Z:(M，w)←→(M'，w')，或者简写为(M，w)←→(M'，w')，并且说w'和w互相模拟对方。

对于基本模态语言，后两条变为:

(ii)'存在LTS到LTS'一个模拟关系为Z1，使得对于所有的v∈W，如果Rwv，那么在W'中存在一个v'使得R'w'v'，并且vZ1v';

(iii)'存在LTS到LTS'一个关系为Z2，且满足是LTS'到LTS的模拟关系，使得对于所有的v'∈W'，如果R'w'v'，那么在W中存在一个v使得Rwv，并且vZ2v'。

在定义2.2中，如果Z1=Z2=Z，则Z就是从M到M'的一种特殊的双模拟——互模拟［2］。

三、有关双模拟的一些事实

定义3.1 M和M'是上述的两个τ－模型，Z是从M到M'的一个双模拟，如果下面的两个条件成立，我们称 M和 M'是双模拟等价的，记作MΞM':

对于每个w∈W，存在w'∈W'，并且wZw';

对于每个w'∈W'，存在w∈W，并且wZw'。

定义3.2 M和M'是任意两个τ－模型，如果下面的条件成立，我们称τ－模型的一个性质φ是双模拟不变的:

如果(M，w)←→(M'，w')并且M，w╞φ，那么M'，w'╞φ。

事实1 模态逻辑不具有双模拟不变性。

也就是说对于非互模拟的双模拟状态来说，我们只要找到模态公式把它们区分开来就足够了，如图1［3］。P1和Q1是双模拟的，很显然P1满足◇□(p∧﹁p)，而Q1不满足◇□(p∧﹁p)，所以这个模态公式不具有双模拟不变性，并因此模态逻辑不具有双模拟不变性。

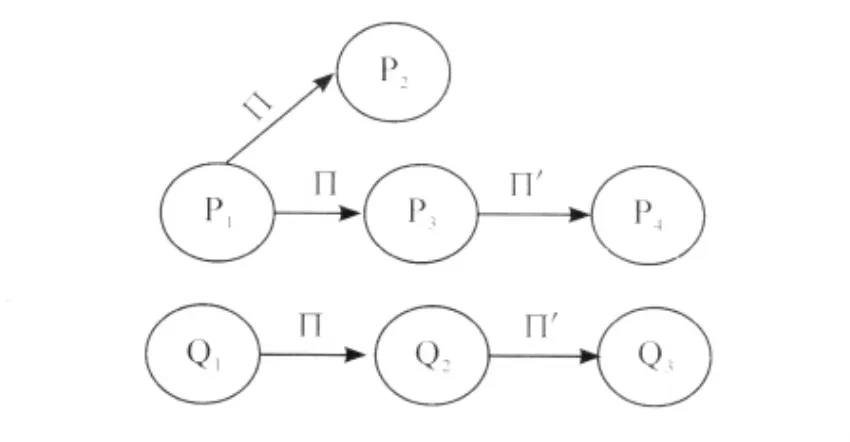
图1 进程间的双模拟关系

事实2 双模拟不必然蕴涵模态等价性。

也就是说，我们可以找到两个状态是双模拟的，但是它们不具有相同的模态理论。这个事实和事实1是同一的，其论证也是相同的。

事实3 在ML(τ，Φ)中，模态等价性不蕴涵双模拟。

对于模态语言ML(τ，Φ)来说，如果对模型不加限制，就有可能出现非双模拟的模态等价性模型，如图2［4］:

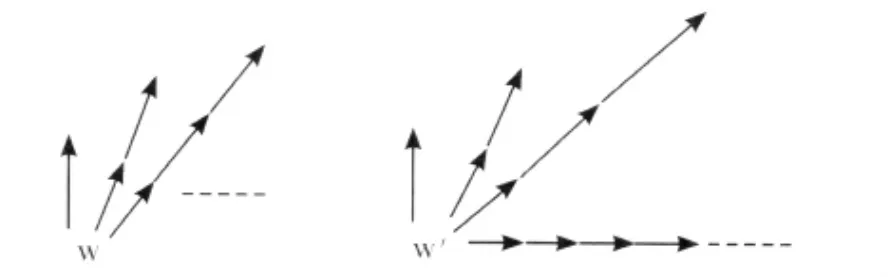
图2 非双模拟的模态等价模型

在上面的两个模型中，对每个n∈N，w一个长度为n的分支，w'除了具有w所有分支外，还有一个无穷分支。很容易证明这两个模型不是“根双模拟”的:虽然w'可模拟w，但w不可模拟w'，因为w'有一个无穷分支，w没有这样的分支。但是在模态逻辑ML(τ，Φ)里，如果假定每个状态满足相同的原子命题，也不难证明它们是模态等价的，即具有相同的模态理论。

在无穷模态逻辑ML∞(τ，Φ)中，我们就可以有下面的定理:

定理3.1 在ML∞(τ，Φ)中，模态等价性蕴涵双模拟。

这个论证是不足道的。我们知道，在ML∞(τ，Φ)中，两个状态(模型)是模态等价的，它们一定是互模拟的，而互模拟蕴涵双模拟，所以在ML∞(τ，Φ)中模态等价蕴涵双模拟。

四、正存在模态公式的双模拟不变性

虽然模态逻辑不具有双模拟不变性，是否有一部分模态公式具有双模拟不变性呢?答案是肯定的，为此我们先给出下面的定义。

定义4.1 如果一个公式是仅仅使用∧、∨和存在模态算子△从命题字母生成的公式，那么该公式被称为正存在模态公式。为将来证明的方便我们把正存在模态公式以及与某一正存在模态公式等价的模态公式统称为正存在模态公式，用MPE表示这一类模态公式。

定义4.2 对于任意的正存在模态公式φ∈MPE，任意的模型M和M'及其任意的状态w和w'，如果M，w╞φ⇔M'，w'╞φ，那么称w和w'是正存在模态等价的。

定理4.1 正存在模态公式是双模拟不变的。

我们只对基本模态语言证明这一结论。

证明:令φ∈MPE是任一正存在模态公式，M和M'是任意的两个模型，w和w'它们的任意状态，且满足存在一个双模拟关系Z使得wZw'。现在我们用归纳法证明M，w╞φ⇔M'，w'╞φ。

当φ=p(命题字母)，由双模拟的定义可知M，w╞p⇔M'，w'╞p。

当φ=φ∨ψ时，M，w╞φ∨ψ⇔M，w╞φ∨M，w╞ψ，由归纳假设M，w╞φ∨M，w╞ψ⇔M'，w'╞φ∨M'，w'╞φ⇔M'，w'╞φ∨ψ。

当φ=φ∧ψ时，M，w╞φ∧ψ⇔M，w╞ψ∧M，w╞ψ，由归纳假设M，w╞φ∧ M，w╞φ⇔ M'，w'╞φ∧M'，w'╞φ⇔M'，w'╞φ∨ψ。

当φ=◇φ时。假设M，w╞◇φ，那么存在一个w的后继v使得M，v╞φ。因为w和w'是双模拟的，所以存在从M到M'的模拟关系Z1使得wZ1w'，再根据模拟的定义可知存在w'的后继v'使得vZ1v'，并因此M'，v'╞φ。所以M'，w'╞◇φ。另一个方向的证明与此相同。

笔者把此定理称之为双模拟不变性定理。此定理只是说明正存在模态公式是双模拟不变的，但是此定理的逆定理是否成立呢?答案是肯定的。在证明此结论之前，先引入一些概念和定理。

定义4.3 令M=(W，R，V)是一个基本模态相似型的模型，X是W的一个子集，φ是一个模态公式集。如果对所有的公式φ∈∑，存在一个状态x∈X使得M，x╞φ，我们称∑在集合X里是可满足的。如果∑的每个有穷子集在集合X里是可满足的，我们就称∑在集合X里是有穷可满足的。对每个状态w∈W和每个模态公式集∑，如果∑在w的后继集是有穷可满足的，那么∑在w的后继集是可满足的，我们称M是m－饱和的。

对任意的模态相似型来说，m－饱和性定义如下:令τ是一个模态相似型，M是一个τ－模型。对M的每一个状态w，每个n元模态算子Δ∈τ和模态公式集序列∑1，…，∑2，如果对每个有穷子集序列Δ1⊆∑1，…，Δn⊆∑n，存在状态v1，…，vn满足Rwv1…vn并且v1╞Δ1，…，vn╞Δn，那么在M中存在状态v1'，…，vn'满足Rwv1'…vn'并且v1'╟∑1，…，vn'╞∑n。我们称M是m－饱和的。

定理4.2 令τ是一个模态相似型。那么m－饱和的τ模型具有Hennessy-Milner性质。这里Hennessy-Milner性质的模型类是指互模拟与模态等价一致的模型类。

证明:见Blackburn《模态逻辑》第92页命题2.54的证明［1］。

如何构造m－饱和的模型呢?通过超滤子扩张。在定义超滤子扩张时需要用到一个框架的幂集代数上的运算，现在我们给出其定义。

定义4.4 令τ是一个模态相似型，F=(W，{RΔ|Δ∈τ})是一个τ－框架，对每个n+1元关系我们定义W的幂集P(W)上的两种运算和mΔ。

mΔ(X1，…，Xn)={w∈W|存在w1，…，wn满足RΔww1…wn并且对所有的i∈n，wi∈Xi}

在基本模态语言中，m◇(X)是可及X的某个状态的点集(X)是只可及X的状态的点集，因此可得对任意的模型M，

V(◇φ)=m◇(Vφ))和V(□φ)=mδ◇(V(φ))

另外，超滤子扩张中还涉及到一个模型上的超滤子概念，所以我们先给出滤子和超滤子的定义。

定义4.5 令W是一个非空集，W上的一个滤子F是满足下列条件的一个集合F⊆P(W):

(i)W∈F;

(ii)如果X，Y∈F，那么X∩Y∈F;

(iii)如果X∈F，并且X⊆Z⊆W，那么Z∈F。

明显地，P(W)本身就是一个滤子。不同于P(W)的滤子被称为真滤子。W上的超滤子是W上的极大真滤子，也就是一个真滤子U且满足对所有的X∈P(W)，X∈U当且仅当WX∉U。

定义4.6 令W是一个非空集，对于任意元素w∈W，由w生成的主要超滤子是由单元素集{w}生成的W上的滤子πw，即πw={X⊆W|w∈X}

定义 4.7 令 τ是一个模态相似型，F=(W，RΔ)Δ∈τ是一个τ－框架。F的超滤子扩张ueF被定义为框架(Uf(W)，{|Δ∈τ})。这里Uf (W)是W上的超滤子集;成立当且仅当对于W上的超滤子n－元组u0，…，un，所有的i (1≤i≤n)，如果Xi∈ui，那么mΔ(X1，…，Xn)∈u0。

一个τ－模型M=(F，V)的超滤子扩张是一个模型ueM=(ueF，Vue)，这里Vue(pi)是包含元素V(pi)的所有W上的超滤子集合，也就是Vue(pi)={u|V(pi)∈u且u是W上的超滤子}。

定理4.3 令τ是一个模态相似型，令M是一个τ－模型。那么对任意的公式φ，W上的任意超滤子u，V(φ)∈u，当且仅当ueM，u╞φ。因此，对M的每个状态w，我们有(M，w)≈(ueM，πw)。

证明:见Blackburn《模态逻辑》第96页命题2.59的证明［1］。

定理4.4 令τ是一个模态相似型，令M是一个τ－模型。那么ueM是m－饱和的。

证明:见Blackburn《模态逻辑》第99页命题2.61的证明［1］。

有了这些定义和定理，就可以证明下面的双模拟不变性定理。

定理4.5 令τ是一个模态相似型，φ是一个τ公式。那么φ是双模拟不变的当且仅当φ是一个正存在模态公式。

证明:正存在模态公式在双模拟下是不变的，见定理3.1。相反，假定φ在双模拟下是不变的，并且考虑φ的正存在模态后承的集合:

MPEC(φ)={ψ|ψ是正存在模态公式，且φ╞ψ}

我们先证明MPEC(φ)╞φ。假设M，w╞MPEC(φ)，我们需要证明M，w╞φ。令

Γ={﹁ψ|ψ是正存在模态公式，且M，w╞/ ψ}。

首先我们断定集合{φ}∪Γ是一致的。因为，假定它不一致，则存在公式﹁ψ1，…，﹁ψn∈Γ，使得╞φ→﹁(﹁ψ1∧…∧﹁ψn)，即φ╞ψ1∨…∨ψn。根据定义，每个公式ψi是一个正存在模态公式，因此，ψ1∨…∨ψn也是一个正存在模态公式。据MPEC(φ)的定义，ψ1∨…∨ψnn∈MPEC(φ)。又根据假设，M，w╞ψ1∨…∨ψn，由此可得出，对某个i(1≤i≤n)，M，w╞ψi。这与M，w╞/ψi矛盾。

因为集合{φ}∪Γ是一致的，我们可以找到一个模型N和N中一个状态v使得N，v╞φ∧∧Γ。显然，对于每一个正存在模态公式ψ，如果N，v╞ψ，则M，w╞ψ。这是因为:N，v╞∧Γ⇒N，v╞Γ，由Γ定义可知，对每一个正存在模态公式ψ，如果M，w╞/ψ，那么﹁ψ∈Γ，所以N，v╞﹁ψ，即N，v╞/ψ。可以从定理3.3推出，对于超滤子扩张ueM和ueN，我们有同样的关系:对每个正存在公式ψ，如果ueN，πv╞ψ，则ueM，πw╞ψ(假设ueN，πv╞ψ，由定理3.3可得N，v╞ψ，由上面的结论M，w╞ψ，再由定理3.3可得ueM，πw╞ψ)。据定理3.4，超滤子扩张是m－饱合的，可证这个关系实际上是一个从ueN，πv到ueM，πw的模拟。

现在证明M，w╞φ。因为N，v╞φ，由定理3.3可得ueN，πv╞φ。因为φ在双模拟下不变的，所以φ在模拟下是保持的，我们得到ueM，πw╞φ。再次根据定理3.3，我们得出结论M，w╞φ。再根据假设M，w╞MPEC(φ)，可得MPEC (φ)╞φ。根据紧致性可知，存在MPEC(φ)的有穷个元素φ1，…，φn，使得{φ1，…，φn}╞φ，即φ1∧…∧φn╞φ。由φ1，…φn是正存在公式知φ1∧…∧φn也是正存在公式并且 φ1∧…∧φn∈(MPEC(φ)，根据MPEC(φ)的定义可知φ╞φ1∧…∧φn，因此╞φ↔φ1∧…∧φn。

五、正存在模态公式的对应定理

由范本特姆刻画定理，我们知道模态逻辑对应了一阶逻辑互模拟不变的部分，那么正存在模态公式对应了一阶逻辑的哪一部分呢?为此，我们首先要引入一系列概念和定理。

定义5.1 令τ是一个模态相似型，Φ是一个命题字母的收集。令L1τ(Φ)是一个含有等词的一阶语言，它由与Φ的命题字母p0，p1，p2，…相对应的一元谓词符号P1，P2，P3，…和τ中的每个n元模态词Δ相对应的n+1元关系符号RΔ构成。我们用α(x)表示只有一个自由变元x的一阶公式。

定义5.2 令x是一阶变元，标准翻译STx是从模态公式到L1τ(Φ)中一阶公式的一个映射，定义如下:

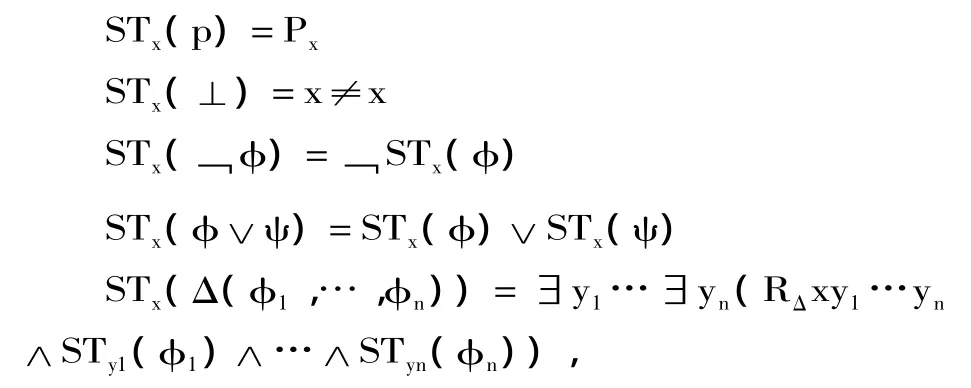
这里y1，…，yn是新变元(也就是至今在翻译中还没使用的变元)。如果使用基本的模态语言，那么最后一个条件化归为:

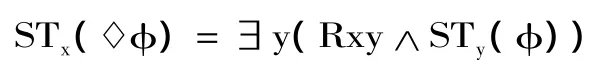
这里R是R◇的简写。

定理5.1 固定一个模态相似型τ，令φ是一个τ－公式。那么:

(i)对所有的模型M和M中的所有状态w，M，w╞φ⇔M╞STx(φ)［w］。

(ii)对所有的模型M:M╞φ当且仅当M╞∀xSTx(φ)。

证明:通过φ上的归纳进行证明，这里略。

定义5.3 令α是一个自然数或ω，M是一个模型，如果对基数小于α的每个子集A⊆W，M的扩张MA满足每个与MA的一阶理论一致的L1［A］－公式集Γ(x)，那么模型M就是α－饱和的。一个ω－饱和的模型通常被称为可数饱和的［5］。

定理5.2 令τ是一个模态相似型，任意可数饱和的τ－模型都是m－饱和的。

证明:见Blackburn《模态逻辑》第102页命题2.65的证明［1］。

定义5.4 令M和N两个模型，其中M的状态集(个体域)为A，N的状态集(个体域)为B，M到N的一个初等嵌入是一个映射f:A→B(记作: f:M≤N)，且满足:对所有的公式α(x1，…，xn)和n元组a1，…，an∈A，M╞α(a1，…，an)当且仅当N╞α(f(a1)，…，f(an))。

定理5.3 令τ是一个模态相似型，并且令M和N是τ－模型，w是M中的状态，v是N中的状态。那么下面是等价的:

(i)对所有的模态公式φ:M，w╟φ当且仅当N，v╟φ。

(ii)存在一个互模拟 Z:ueM，πw←→ueN，πv。

(iii)存在可数的饱和模型M*，w*和N*，v*，及初等嵌入f:M≤M*和g:N≤N*满足:

(a)f(w)=w*和g(v)=v*

(b)M*，w*←→N*，v*。

这个定理也叫 Detour引理，定理的证明见Blackburn《模态逻辑》第 102页命题 2.66的证明［1］。

定义5.5 令α(x)是语言L1τ(Φ)的一个一阶公式，如果对任意模型M和N，M中的任意状态w，N中的状态任意状态v及M和N之间的双模拟Z使得wZv，我们有M╞α(x)［w］当且仅当N╞α(x)［v］，那么我们称α(x)是双模拟不变的。

有了这些定义和定理，就可以证明下面的正存在模态公式对应定理:

定理5.4 令α(x)是L1τ(Φ)的一个一阶公式，α(x)是双模拟不变的当且仅当它(等价于)一个正存在模态τ－公式的标准翻译［6］。

证明:从右到左的方向的证明很简单，如果α (x)等价于一个正存在模态τ－公式φ的标准翻译，因为正存在模态公式是双模拟不变的，所以α (x)也是双模拟不变的。

为了证明从左到右的方向，假设α(x)是双模拟不变的，并且考虑α的正存在模态后承的标准翻译集:

STx［MPEC(α)］={STx(φ)|φ是一正存在模态公式，并且α(x)╞STx(φ)}。

我们首先证明STx［MPEC(α)］╞α(x)。假定M╞STx［MPEC(α)］［w］，我们需要证明M╞α(x)［w］。

令Γ(x)={STx(﹁ψ)|ψ是正存在模态公式，且M，w╞/ψ}={﹁STx(ψ)|ψ是正存在模态公式，且M，w╞/ψ}。

现在我们证明Γ(x)∪{α(x)}是一致的。假定它不一致，则存在公式﹁STx(ψ1)，…，﹁STx(ψn)∈Γ (x)使得α(x)╞﹁(﹁STx(ψ1)∧…∧﹁STx(ψn))，即α(x)╞STx(ψ1)∨…∨STx(ψn)。所以对某个ψi(1≤i≤n)，α(x)╞STx(ψi)。由于ψi是一个正存在模态公式，根据STx［MPEC(α)］的定义可知，STx(ψi)∈STx［MPEC(α)］。由假设可知，M╞STx(ψi)［w］，根据定理4.1，M，w╞ψi，这与﹁STx(ψi)∈Γ(x)矛盾。

因为集合Γ(x)∪{α(x)}是一致的，我们可以找到一个模型N和N中一个状态v使得N╞(∧T(x)∧α(x))［v］。显然，对于每一个正存在模态公式ψ，如果N，v╞ψ，则M，w╞ψ。这是因为:M，w╞/ψ当且仅当﹁STx(ψ)∈Γ(x)，因此N╞﹁STx(ψ)［v］，即N╞STx(﹁ψ)［v］，N，v╞﹁ψ，即N，v╞/ψ。

我们可以部分使用Detour引理来证明我们的结论。由定理4.3知，存在两个可数饱和模型M *，w*(初等嵌入f:M≤M*)和N*，v*(初等嵌入f:N≤N*)，并且对所有的正存在模态公式ψ，如果N*，v*╞ψ，那么M*，w*╞ψ。因为可数饱和模型是m－饱和的，可证这个关系实际上是一个从N*，v* 到M*，w*的模拟。

现在我们来证明M╞α(x)［w］。因为N╞α(x)［v］，根据初等嵌入，所以N*╞α(x)［v *］，因为α(x)是双模拟不变的，所以是模拟保持的，于是M*╞α(x)［w*］。再根据初等嵌入的性质，所以M╞α(x)［w］。所以STx［MPEC(α)］╞α(x)。

现在证明α(x)等价于某个正存在模态公式的翻译。因为STx［MPEC(α)］╞α(x)，根据一阶逻辑的紧致性定理，对于STx［MPEC(α)］的有穷子集X，我们有X╞α(x)。所以╞∧X→α(x)。不足道地╞α(x)→∧X，因此╞∧X↔α((x)。因为每一个β∈X是某个正存在模态公式的翻译，所以∧X也是正存在模态公式的翻译。

［1］Blackburn P，De Rijke M，Venema Y.Modal Logic［M］.New York:Cambridge University，2001:64－112.

［2］李娜，姚从军.互模拟的一些基本性质［J］.云南师范大学学报，2010(5):70－71.

［3］Sangiorgi.Bisimulation and coinduction:behavious，fixedpoints［M］.unpublished manuscript，2009:15.

［4］姚从军.走进模态逻辑的互模拟［J］.科学技术哲学研究，2010(3):38－39.

［5］王世强.模型论基础［M］.北京:科学出版社，1984: 145－146.

［6］姚从军.互模拟理论的逻辑研究［D］.天津:南开大学哲学院，2011.

Two-Way Simulation and Modal Logic

YAO Cong-jun
(Department of politics Hunan University of Sicence and Engineering，Yongzhou 425100，China)

The author defines the concept of two-way simulation on the basis of simulation in kripkle model，and gives the definition of two-way simulational modal invariability and modal equivalence，and discusses on the relationship between the modal logics and two-way simulation;Futhermore，the autuor analyses the relations between the modal equivalence and two-way simulational modal invariability with respect to ML(τ，Φ)and ML∞(τ，Φ);Finally，the autuor proves the relation between the positive existential modal formulas and two-way simulation，and characterize the positive existential modal formulas as the two-way simulational invariable first-order formulas.

simulation;two-way simulation;modal logic;positive existential modal formula;twoway simulational modal invariability

B81

A

1674－8425(2011)08－0077－06

2011－06－06

国家社科基金“超集、互模拟以及在模态逻辑、计算机科学中的作用研究”(08BZX049)资助项目。

姚从军(1971—)，男，湖北随州人，哲学博士，湖南科技学院思政部讲师，中国社会科学院哲学所博士后，研究方向:现代逻辑、语言逻辑。

(责任编辑 魏艳君)