考虑剪切变形波形钢腹板组合箱梁抗弯刚度实用计算方法

李世深 孙斌

1 广西大学土木建筑工程学院，广西 南宁 530004

2 中铁二十工程局集团第四工程公司，山东 青岛 266061

考虑剪切变形波形钢腹板组合箱梁抗弯刚度实用计算方法

李世深1孙斌2

1 广西大学土木建筑工程学院，广西 南宁 530004

2 中铁二十工程局集团第四工程公司，山东 青岛 266061

本文假设组合箱梁的弯矩M全部由翼板来承担，剪力Q由波形刚腹板来承担，按照考虑剪切变形的Timoshen梁ko弯曲理论，推导出考虑波形刚腹板剪切变形的弯曲刚度计算式，在此基础上，将弯矩M按三角级数展开并近似取第一项，利用三角函数导数性质，得到简单的考虑波形刚腹板剪切变形对抗弯刚度折减系数表达式。通过验证模型，验证了这种等效在集中荷载和均布荷载下具有良好的精度。

波形刚腹板；组合箱梁；抗弯刚度；实用计算方法

引言

波形钢腹板组合箱梁由两种不同性质的材料组成，同时，波形钢腹板具有纵向褶皱效应[3]，其抗弯抗扭刚度计算跟传统箱梁有区别，而结构刚度在设计计算或者研究分析中会涉及，本文分析波形钢腹板组合箱梁弹性阶段抗弯和抗扭刚度，为弯扭分析作准备。

1 考虑波形钢腹板剪切变形对截面抗弯刚度的折减系数

图1是一个波形钢腹板组合箱梁简支梁桥及断面。如图2，在计算竖向挠度V时，把梁看成这样的整体梁式受力构件：弯矩M由翼板完全承受，剪力Q由波形钢腹板承受[1]。

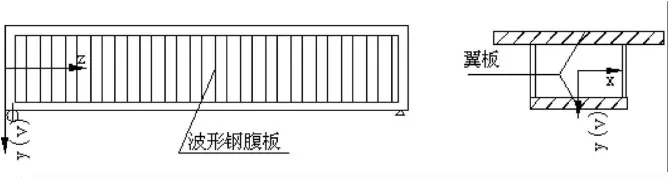
图1 波形钢腹板组合箱梁简支梁桥及断面

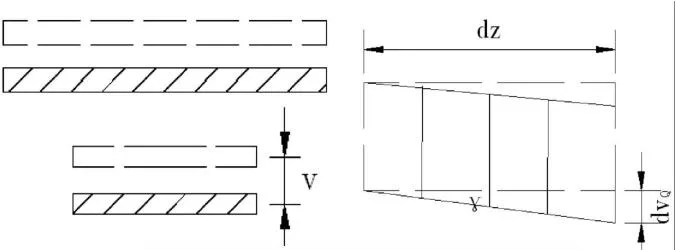
图2 竖向挠曲位移

竖向挠度V由两部分组成：由作用于翼板的弯矩M所产生的挠度VM，及作用于波形钢腹板的剪力Q所产生的挠度VQ。VM可以按照初等梁理论进行计算，而计算VQ时假设截面上剪应力均匀分布，计算图示如图2：

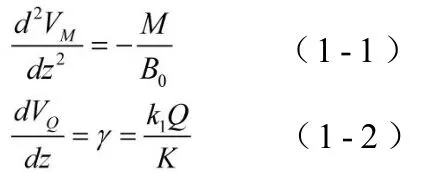
其中，B0为只考虑混凝土翼板面积的截面抗弯刚度，下文简称为未折减刚度。如图2所示，设上、下翼板面积分别为F1和F2，到中性轴的距离分别为h1和h2，忽略翼板截面绕本身形心轴的惯性矩，则：

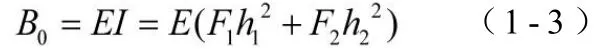
将式（1-1）和式（1-2）代入下式：

其中，B为考虑波形钢腹板剪切变形的截面抗弯刚度，下文简称折减后刚度。

比较式（1-5）和式（1-6）得：

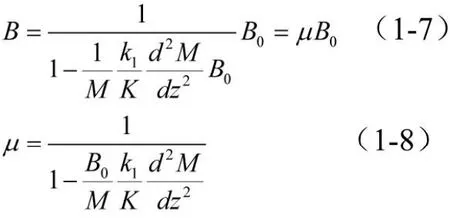
μ为考虑波形钢腹板剪切变形对截面抗弯刚度的折减系数。

由μ的表达式可以看到，μ与波形钢腹板抗剪刚度与翼板抗弯刚度之比K/B0有关；μ与波形钢腹板剪应力分布，即剪应力分布不均的校正系数k1有关。

μ还与截面的弯矩M有关，而弯矩M是坐标z的函数，所以μ也是坐标z的函数；截面截面的弯矩M(z)由约束条件和力边界条件确定，跨中作用有集中荷载的简支梁，弯矩M(z)为双折线；满跨分布均布荷载的简支梁，弯矩M(z)为抛物线；分布荷载p(z)为坐标z的一次或者更高次函数，弯矩M(z)将会是三次或者以上抛物线。在分析计算中，每次都根据截面弯矩M(z)来确定μ显得比较麻烦。鉴于实际荷载为离散随机分布，截面弯矩M(z)分布规律复杂，在实际分析中，我们可以将截面弯矩M(z)按三角级数进行展开，利用三角函数导数性质，得到μ的实用计算方法：

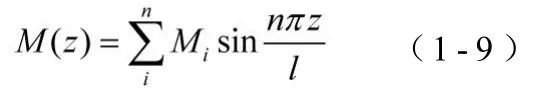
近似取第一项，并令展开弯矩M(z)与实际弯矩在跨中相等，得

将式（1-1 0）代入式（1-8）得

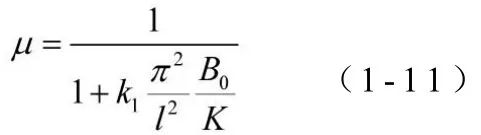
2 荷载分布差异的影响分析

弯矩M(z)按三角级数进行展开，项数取得越多就能越精确满足荷载边界条件，而式（1-11）是只取一项的情况，其不能精确满足荷载边界条件，而只能近似等效，实际上，式（1-11）要求荷载边界应为正弦分布荷载。当荷载为集中荷载或是均布荷载时，式（1-1 1）只能近似的计算，为了说明这种近似计算带来的误差在工程中是可以接受，计算结果也是偏于安全的，采用模型进行分析，该模型是文献[2]的试验模型。

按照经典梁理论[4]，并引入抗弯刚度折减系数μ，得到简支梁的荷载、跨中挠度和抗弯刚度三者的关系式为：

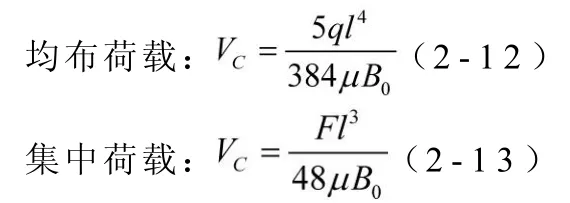
其中B0是只考虑混凝土翼板面积的截面抗弯刚度，为不计腹板剪切变形影响的截面抗弯刚度，下文简称为未折减刚度，此时μ =1；

当μ按照式（1-11）计算时，μB0表示考虑波形钢腹板剪切变形的截面抗弯刚度，也为本文提出抗弯刚度近似计算方法，下文有提到本文方法系按照式（1-11）的近似计算，考虑波形钢腹板剪切变形的截面抗弯刚度下文亦简称为折减后刚度；

提出这样的假设在试验或者有限元分析时，荷载、跨中挠度和抗弯刚度总遵循着式（1-1 2）和式（1-1 2）计算格式，剪切变形或者其他影响因素都归结到抗弯折减系数μ上，B0始终为只考虑混凝土翼板面积的截面抗弯刚度，而不同方法μB0代表的意义就不同。通过试验可以得到梁的荷载与跨中挠度，将其代入式（1-12）和式（1-12），这样可以计算出刚度μB0，此时μB0的意义为截面的实际抗弯刚度；有限元分析亦可以得到不同荷载等级下跨中节点的位移，也将其代入式（1-12）和式（1-12）得到有限元的刚度μ B0。

(1) 验证模型

为文献[2]的试验模型。模型尺寸，如图3所示。波形钢腹板尺寸：波高为24mm，波长为144mm，斜板段长度32 mm和直板段长度40mm，板厚为2mm，板的高度为307mm。

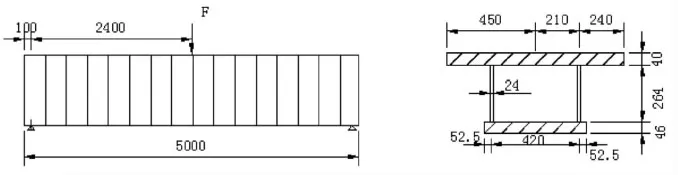
图3 模型尺寸（单位:mm）

材料性质列于表1。

表1 材料性质

建立有限元模型：本节分析的是波形刚腹板剪切变形的影响，单元选择应能够保证剪切变形得到正确模拟，shell181可以考虑剪切变形影响的单元，所以采用shell181来模拟波形钢腹板，而混凝土翼板比波形钢板厚，采用和shell181同阶的实体单元solid45来模拟；不考虑预应力筋作用；利用对称性，只建立1/ 4模型，在对称面施加对称约束即可。模型的约束边界条件为简支，所以只约束支座处节点x，y方向的平动自由度，z方向可以自由伸缩；集中力等效为一定面积内分布荷载，以避免应力集中。模型采用映射网格划分，总共3260个solid45单元，245个shell181单元。图4为有限元模型。

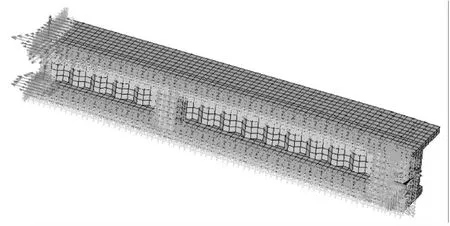
图4 试验模型Ⅰ有限元模型

（a）跨中集中荷载

本节分析波形钢腹板剪切变形对截面抗弯刚度的折减问题，原则上只要通过式（1-12）和式（1-13）获得试验或者有限元模型的抗弯刚度即可，但为了更直观反映剪切变形影响的规律，我们用未折减刚度和折减后刚度，通过式（1-1 2）和式（1-1 3）计算各荷载等级下不计腹板剪切变形对抗弯刚度折减的挠度值和本文方法计算的挠度值，并将其与有限元法的挠度值、试验挠度值列于表2进行比较。

表2 简支梁受跨中集中荷载的挠度比较

其中，试验挠度值为文献[2]的试验数据。有限元法的挠度值是提取有限元模型跨中底板中间节点和波形刚腹板两侧节点，共三个节点的y方向位移平均值。

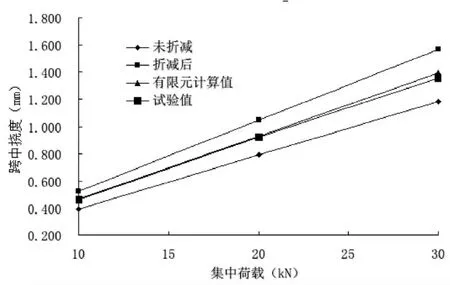
图5 模型Ⅰ集中荷载—跨中挠度曲线

从图5荷载—跨中挠度曲线图可以看出：在试验荷载范围内，简支梁跨中挠度值与荷载是线性关系，说明简支梁在试验加载过程中还处于弹性阶段；有限元模型计算结果与试验数据基本吻合。

验证模型的剪跨比为1/13.7＜1/10，在相同的荷载等级下，刚度未折减的挠度值比试验和有限元的挠度值偏小，误差为14.8%，说明在此剪跨比下，波形钢腹板剪切变形仍引起截面的抗弯刚度较大折减，而忽略剪切变形影响计算得到的截面抗弯刚度偏于刚性。

从式（1-13）看出，截面刚度EI正比于荷载与挠度的比值F/VC，因此，荷载—跨中位移曲线各个直线斜率的比值就是截面的刚度比。取未折减的截面抗弯刚度为1，可以求得折减后刚度为0.757，试验刚度为0.848，有限元刚度为0.857。将试验刚度当做简支梁的实际抗弯刚度，比较折减后截面抗弯刚度与实际抗弯刚度的差值，就可以得到采用式（1-11）近似计算引起的误差。在集中荷载作用下，验证模型采用式（1-11）计算折减后刚度比实际抗弯刚度要小10.7%。而未折减抗弯刚度比实际抗弯刚度大17.9%。若不考虑刚度折减，偏于刚性，考虑刚度经折减后，偏于柔性，且误差值较小，说明此例可采用式（1-11）给出的折减系数计算抗弯刚度。

(b)均布荷载

仍采用试验模型Ⅰ，将集中荷载转化为沿垮均匀分布的线荷载，荷载等级分为2.083N/mm，4.166 N/mm，6.249 N/ mm。挠度计算结果列于表3。

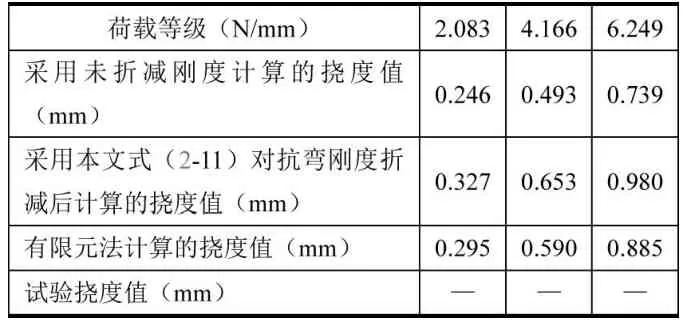
表3 简支梁受均布荷载的挠度比较

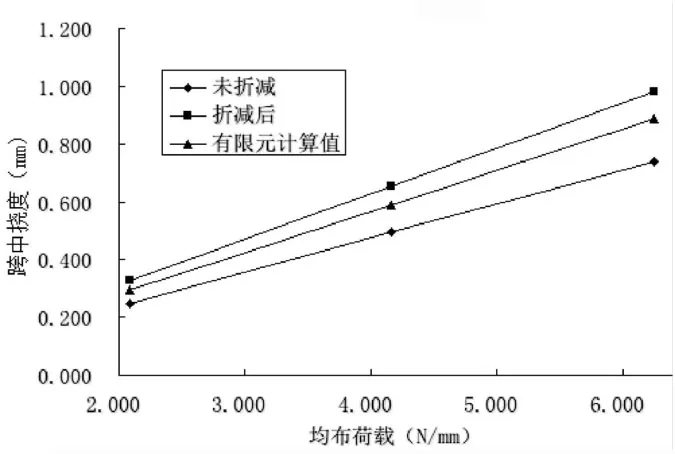
图6 模型Ⅰ均布荷载—跨中挠度曲线

仍采用前面的方法，取未折减的截面抗弯刚度为1，可以求得折减后刚度为0.754，有限元计算的刚度为0.835。在均布荷载作用下，验证模型采用式（1-11）对刚度进行折减后比实际抗弯刚度要小9.7%。而未折减抗弯刚度比实际抗弯刚度大19.8%。均布荷载作用下，本例采用式（1-11）计算截面抗弯刚度误差较小，且结果偏刚性。

从图5和图6可以得到可以看出这样的规律：试验模型无论是在集中荷载还是均布荷载作用下，未折减截面抗弯刚度偏大，而考虑剪切变形折减后结构刚度偏小，未折减和折减后两条荷载—跨中挠度曲线包络着有限元计算得到的荷载—跨中挠度曲线。折减后的曲线与有限元的曲线比较靠近，说明采用式（1-11）给出的折减系数计算抗弯刚度都有较好的精度。

3 结论

本文按照考虑剪切变形的Timoshenko梁弯曲理论推导出，考虑波形刚腹板剪切变形的挠度计算式和刚度计算式，在此基础上，将弯矩M按三角级数展开并近似取第一项，利用三角函数导数性质，得到简单的考虑波形刚腹板剪切变形对抗弯刚度折减系数表达式。计算方法最大特点是使用简单的正弦分布荷载来等效实际复杂随机的荷载分布，通过验证模型，验证了这种等效在集中荷载和均布荷载下具有良好的精度。实际荷载分布具有随机离散性，其分布引起的内力较集中荷载和均布荷载都要接近于正弦分布规律，或者研究中需要将位移或者内力按照三角级数的情形，计算精度将进一步提高。

[1]水口和之，等.本谷桥的设计与施工.桥梁基础[M].1998（9）2-10

[2]王文.波形刚腹板箱梁扭转效应和畸变效应的分析与模型试验研究[D].湖南大学.2007.5

[3]Mohamed Elg，aaAlynand Sesha，driRobert W.Hamilton Bending Strength of Steel Beams with Corrugated We.bsJ[oJ]urnal of Structural Engineering, Vol.123, No.6, June 1997, pp.772-782

[4]孙训方，方孝淑，关来泰.材料力学（Ⅰ）[M].北京：高等教育出版社.2001

10.3969/j.issn.1001-8972.2011.12.022

李世深(1984-)，男，工学硕士，广西崇左市，广西大学土木建筑学院。