Au(110)表面结构和氧原子吸附的第一性原理研究*

王芒芒 宁 华 陶向明 谭明秋

(浙江大学物理系，杭州 310027)(2010年4月18日收到;2010年6月24日收到修改稿)

Au(110)表面结构和氧原子吸附的第一性原理研究*

王芒芒 宁 华 陶向明 谭明秋

(浙江大学物理系，杭州 310027)(2010年4月18日收到;2010年6月24日收到修改稿)

用密度泛函理论(DFT)研究了金属Au(110)表面结构以及氧原子的吸附状态.计算得到Au(110)-(1×2)缺列再构表面原子的弛豫分别是 －15.0%(Δd12/d0)和 －1.1%(Δd23/d0)，表面能为52.7 meV/2，功函数 Φ =5.00 eV;Au(110)-(1×3)缺列再构表面的 Δd12/d0= －20.5%，Δd23/d0=+2.7%，表面能 53.4 meV/2，Φ =4.98 eV.计算模拟了它们的STM图像并记录了STM针尖的起伏变化.研究发现Au(110)-p(1×1)和p(1×2)再构表面的氧吸附，在高覆盖下各吸附位置的吸附能值均为负值，发生的吸附可视为吸热过程.说明Au(110)表面基本上与氧不发生吸附和反应，具有很高的化学惰性.

缺列再构Au(110)表面，STM图像，氧原子吸附

PACS:73.20.－ r，68.35.－ p，68.37.Ef，68.43.Fg

1.引 言

通常我们认为贵金属金具有化学惰性，在空气中很难被氧化.但是实验上发现粉末状的金颗粒，在低温下一氧化碳氧化以及其它催化反应，如乙炔氢氯化反应中，却表现出非常活跃的催化性质［1，2］.Haruta等人［3］第一次指出金催化CO氧化的温度甚至可以低达70 K就可以发生.特别是金在 TiO2，α-Fe2O3和Co3O4中，显示出非常活跃的低温催化特性［4］.而对这些反应的第一性原理研究还是比较少的.因此对金表面以及有关吸附问题在固体表面物理和化学的研究中具有重要的意义.

Sault等人［5］研究了压强为 1400 Torr(1 Torr=1.33322×102Pa)，温度处于300至500 K时 O2吸附于Au(110)-(1×2)(缺列再构)表面的情况，结果没有观察到任何游离氧吸附.为了产生化学吸附氧，采用了很多方法，如热解离［5，6］，氧离子喷射［7］和微波放电［8］等.Gottfried 等人［9—11］通过电子炮轰氧分子物理吸附层，在 Au(110)-(1×2)上产生了化学吸附氧.现在已经发现 Au(110)-(1×2)表面将会经历两次相变——在 T=650 K时，发生易兴(Ising)相变，在此过程中会有表面解构;在 T=700 K时［12，13］发生三维粗糙化相变，将伴随着二维表面解构.此外，在清洁表面会发生更深的缺列(第二层原子缺失)和(1×3)周期性的表面再构［14，15］，而且在 350 K 时，此再构表面会稳定增长［14］.通过高温扫描隧道显微镜(STM)［15，16］证实Au(110)-(1×3)稳定增长的温度可达500 K.在Au(110)缺列表面的重构推动力的研究中，发现金的重构趋向与5d金属铱(Ir)和铂(Pt)一样，与相对论效应有关［17］.另外，也有人认为金的相对论性质［18，19］可能与表面重构的共同起源和金链结构的形成有关［20，21］.最近，一些研究表明，氧不仅稳定了Au纳米链的形成，而且显著提高了银链的形成稳定性.

最近Landmann等人［22］在理论上比较系统地研究了Au(110)-(1×r)(r=1—3)表面结构和不同氧覆盖度下的能量，得到如下结论:表面能大小排列顺序缺列再构的表面能最小;在氧吸附中，高氧覆盖下，吸附能值均为负，只有在低氧覆盖下，短桥位(short bridge，SB)和赝三度对称位(pesudothreefold，PT1)的吸附能值出现正值.赝三度对称位的吸附能相较短桥位的吸附能大.另外，他们还研究了 Au(110)-(1×r)表面上链状 Au-O结构［23］，发现在 Au(110)表面最稳定氧吸附的两种不同的链状结构——对称和非对称Au-O链结构.基于原子热力学理论，在Au(110)-(1×2)重构表面上，这两种结构都非常稳定;而在(1×3)表面上，非对称链在低氧化学势情况下，变得稳定.

在本文中，我们将采用第一性原理研究 Au(110)-p(1×2)和p(1×3)缺列再构表面的弛豫特性、功函数，表面能和STM图像等，以及 Au(110)-p(1×1)和p(1×2)再构表面的氧吸附情况.

2.计算方法

我们的密度泛函总能计算是在 Perdew，Burke和Ernzerhof提出的广义梯度近似(GGA)［24］下进行的，使用了维也纳从头计算模拟程序包［25］(Vienna ab initio simulation package，VASP).VASP 是一个进行第一性原理的量子力学分子动力学模拟的复合程序包，采用超软赝势(ultrasoft pseudopotential，USPP)［26］或投影子缀加平面波(projector-augmented wave，PAW)［27］并以平面波为基函数进行总能和电子结构的计算.这是一个高效的平面波赝势程序包，被广泛应用于表面的原子核电子结构的计算［28］.本文在计算中采用了 VASP 版本［29］的 USPP势.我们在研究 Au(110)-(1×2)缺列再构的表面性质时，选用了七层 Au(110)原子层构成层晶(slab)结构来模拟表面，其中六层是基底金原子，最上面一层是表面金原子.表面另外一边的四层作为衬底是固定的，而其余的三层在结构优化计算中是可以变化的，用来模拟表面原子的弛豫.计算 Au(110)-(1×3)结构时，slab选用八层原子来模拟，底下五层是固定的，顶部三层原子是弛豫的.在z方向周期性排列的相邻slab之间留有厚度超过1.0 nm的真空区域，以避免层晶之间的干扰，而实际做STM图像模拟时，需要增大这个距离以保证针尖处的局域电荷密度值来源于它最近的表面.我们对这些设置进行了必要的数值检验，结果表明这个结构模型足以保证计算的精确度，又不至于使计算量过于庞大.在本次计算中，金的晶体结构参数用上述VASP代码进行优化，得到 a=4.176 ，比实验值4.078［30］大了约 2.4%.

Au(110)-(1×2)的计算采用了28×10×1的布里渊区(BZ)网格，用 Monkhorst-Pack(MP)方案［31］自动产生的不可约K∥点数目为70.而对于Au(110)-(1×3)的计算，采用了14×4×1的k空间网格密度.原子平衡位置的搜索使用了 Hellman-Feynman力的共轭梯度(CG)算法［32］，结构优化中的总能收敛判据为10－6eV，Hellman-Feyman原子力的收敛判据为10－2eV/ ，平面波展开的截止能量为250.0 eV.在有关氧原子吸附的计算中，平面波展开的截止能量被设置为500.0 eV.

在考虑Au(110)表面的氧吸附时，对于p(1×1)结构，用于表面计算的 slab选用七层Au(110)原子层构成，对于p(1×2)缺列再构结构，slab选用八层Au(110)原子层，底下四层固定.我们是以1/2O2为基准的.我们计算得到的氧分子中每个氧原子的结合能为 1/2EO2=2.81 eV，氧分子的键长 r0=1.40 ，与 实 验 值 1/2EO2=2.56 eV［33］，r0=1.21［34］基本相符.

3.计算结果及分析

3.1.清洁Au(110)的表面性质

我们计算了 Au(110)，p(1×2)和 p(1×3)表面缺列再构的原子位置的弛豫特性、表面能和功函数，并与其他理论计算结果做了对比(见表1).它们的原子结构示意图见图1.计算弛豫清洁表面的表面能σ的公式计算如下:

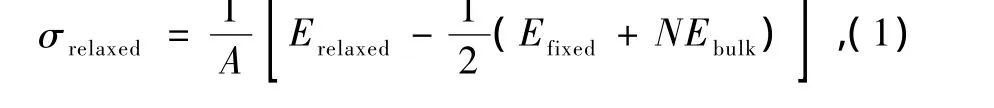
其中 Ebulk，Erelaxed和 Efixed分别是固体中每个金原子的总能，弛豫表面和非弛豫表面的总能.A是一个slab元胞的表面积.本工作中，Au(110)-(1×2)结构的 N=12，p(1×3)结构的 N=18.Au(110)-(1×2)缺列再构表面的弛豫结果为 Δd12=－0.22 ，Δd23= －0.02 ，与文献［22］，X-ray和 LEIS相比，有一定差距，Δd12的差距值为0.1 和0.07 .但是我们计算得到的 Δd12=－0.22 ，与 LEIS(Δd12=－ 0.20)［36］，MEIS(Δd12= － 0.26)［37］和 LEED(Δd12=－0.22)实验数据更符合.Au(110)-(1×3)缺列再构表面弛豫结果为 Δd12=－0.29 ，Δd23=+0.03 ，与文献［22］的计算结果较为接近，与MEIS(Δd12= － 0.32)［40］更为接近.Au(110)-(1 ×2)，Au(110)-(1×3)缺列再构表面的表面能分别为σrelaxed=52.7 meV/2，σrelaxed=53.4 meV/2.用 PE实验得到Au(110)的功函数Φ=5.37 eV.可以看到本文研究得到的Au(110)-(1×2)和(1×3)表面功函数计算结果分为5.00 eV和4.98 eV，与PE实验 得到的结果较相近.

表1 清洁Au(110)-(1×2)表面的弛豫特性、表面能和功函数的比较

图1 (a)Au(110)-(1×2)缺列再构的俯视图(［1］方向上，表层原子缺失一列);(b)Au(110)-(1×3)缺列再构的俯视图(［1 10］方向上，表层原子缺失两列，第二层原子缺失一列).颜色越深表示原子层越深

3.2.Au(110)表面 p(1×2)和 p(1×3)结构的STM模拟图像

STM图像计算的一般理论有Tersoff和Hamann［41］提出.随着第一性原理计算方法的不断改进和提高，已经有可能在密度泛函理论计算结果的基础上对STM图像直接进行计算，有关细节可以参阅文献［42］.根据这个方法，我们计算了Cu(100)c(2×2)/N表面的 STM的线扫描(line scan)的形貌图，得出了和实验结果非常一致的起伏高度［43］，从而圆满地解决了有关表面原子结构问题的实验分歧.

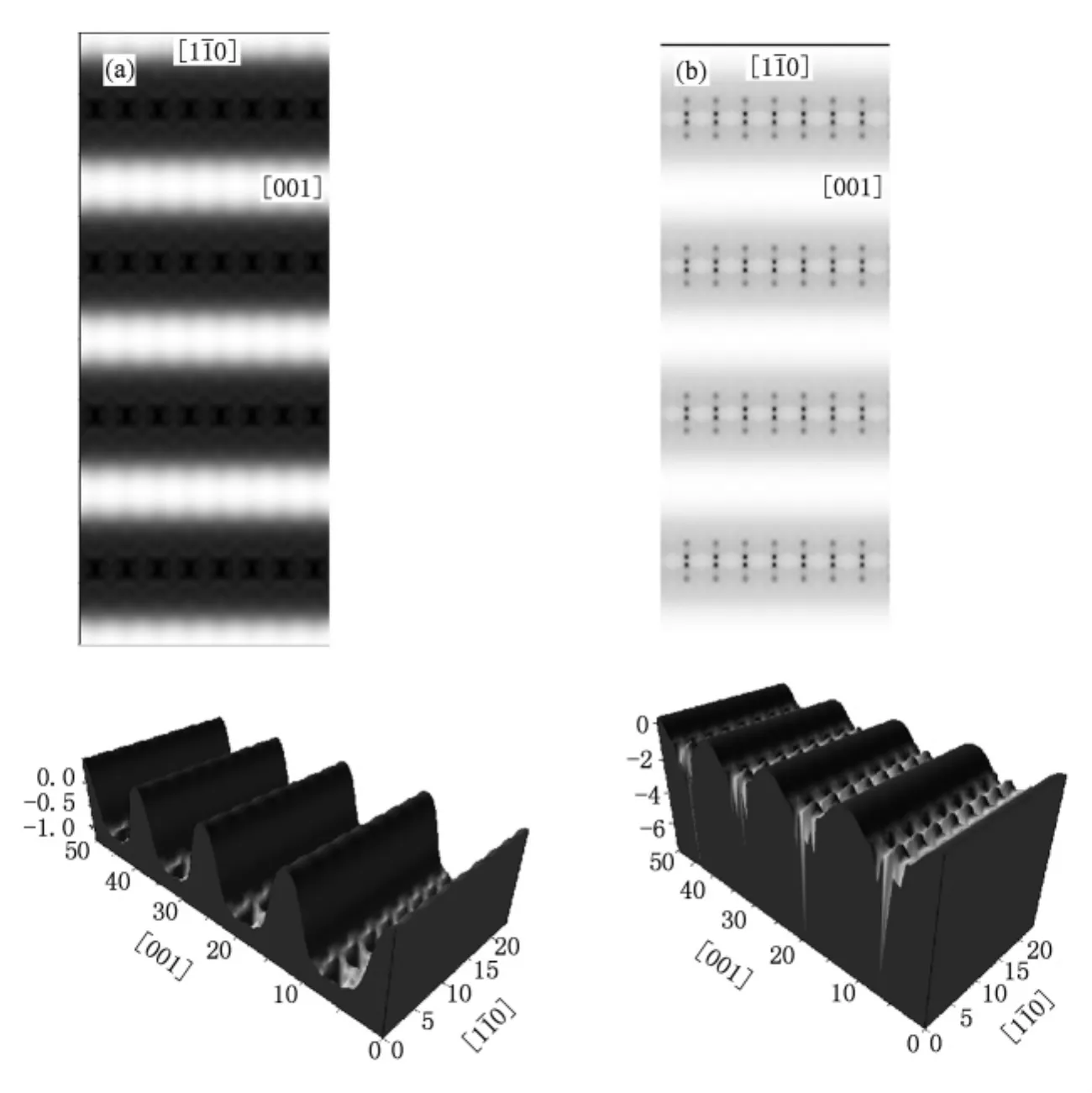
图2 STM模拟图像 (a)针尖高度=3.0 ，Vbias=－0.1 V;(b)针尖高度=5.0 ，Vbias=－0.1 V

图3 Au(110)-(1×2)缺列再构表面的STM模拟图像 (a)STM形貌图;(b)5.0 针尖高度几种偏压下的线扫描

利用上面描述的方法，计算了在不同偏压 V下，针尖相对于表面Au原子高度为 h时，Au(110)-(1×2)(h=5.0 )和 p(1×3)(h=3.0 )缺列再构结构的 STM图像，主要结果在图3，4中给出.在STM图像计算中，需要考虑到STM针尖附近的空间电荷密度，而这个位置往往距离表面5.0 左右.而在Au(110)-(1×3)缺列再构结构中，针尖高度设置为3.0 ，我们是将表面原子看成是吸附物，衬底相当于是第三层原子层.如果将针尖高度仍旧设置成5.0 左右，即从表面原子开始算起，我们得到的STM模拟图像如图2(b)所示，图像异常.这是因为针尖太高，探测不到 Au(110)-(1×3)缺列再构结构中较低层的原子.

所有的偏压以样品上所加偏压为准，这样负偏压测量到的是样品的电子占据态的性质.相应的，样品正偏压表示电子从针尖流向衬底，此时探测到的是样品中未占据的空态性质.图中黑色区域代表针尖起伏比较低的位置，白色区域表示针尖起伏高的位置.通过计算偏压Vbias在－1.0到－0.1 V范围内(电子占据态)，图3(a)和图4(a)中Au(110)-(1×2)和Au(110)-(1×3)缺列再构表面的STM形貌图显示出亮斑形成带状条纹，而两个亮条纹之间有一个暗条纹，彼此间隔排列.这是由于［10］方向的原子的缺失，从而形成间隔的亮暗带状条纹.对比两者STM形貌图，可以看到 Au(110)-(1×3)的STM图像中暗条纹比较宽，这是因为 p(1×3)在［10］方向上，表层缺失两列原子，次表层缺失一列原子.我们在计算模拟STM图像时，也模拟记录了STM针尖的起伏变化，见图3(b)和图4(b).在［10］方向上的槽沟，表示这列原子的缺失，与STM形貌图是稳和的.图5给出了 Au(110)-(1×2)和Au(110)-(1×3)，在不同偏压下的 STM扫描时针尖最大起伏和偏压的关系.Au(110)-(1×2)针尖最大起伏高度大约在0.904—0.948 之间，Au(110)-(1×3)针尖最大起伏高度大约在1.596—1.777 之间，两者波动不大.与STM扫描的针尖起伏相比，表2中Au(110)-(1×2)和Au(110)-(1×3)缺列再构表面的缺列深度，与STM扫描的针尖起伏相比较大.这是因为STM探测到的是表面原子的电荷密度，而不是真实的原子表面，同时由于原子缺列，电荷密度重新分布.事实上，有时要根据实际情况判断，我们组曾做过吸附 Ag(100)表面时的STM模拟图像，发现在缺列再构模型下，表面上被吸附的氧原子在STM扫描下表现为透明的［44］.我们希望，以上STM图像的模拟研究为实验工作者提供了一定的图像信息和理论支持.

3.3.Au(110)表面的氧原子吸附的第一性研究

在 Au(110)表面 p(1×1)结构和 p(1×2)缺列再构结构吸附氧原子中，我们考虑了五种吸附位置:短桥位(short bridge，SB)，长桥位(long bridge，LB)，顶位(top.TP)，谷位(hollow，HL)，赝三度对称位(pseudothreefold，PT)，如图6所示.计算吸附能采用了如下公式:

其中EO2是孤立氧分子的总能，EAu-O是 Au(110)表面吸附氧原子系统的总能.

如表3所示，各位置的吸附能值均为负值，我们将这种吸附看作是吸热的过程.相反的，正的吸附能过程认为放热的过程.Au较于其他金属(Cu［45］，Ag［44］和 Ir［46］)更难发生氧吸附.本文的计算表明，在目前覆盖度的条件下，所有的氧原子吸附位置都是负吸附能(以氧分子作为参考点)，说明氧原子的吸附不是一个可以从氧分子出发自发分解的过程.由于在0.5 ML覆盖度下的PT1位置的吸附能的数值最小，说明这个位置的吸附在此覆盖度下具有最大的吸附能.我们推测，在更低的氧原子覆盖度下，这个位置的吸附能(相对于氧分子)可能变为正值，那么氧分子自发分解的吸附最可能发生在这个位置，这与文献［22］得出的结论一致.而且在文献［22］中，已经计算出在低氧覆盖度下，SB和PT1的吸附能值最先出现正值.

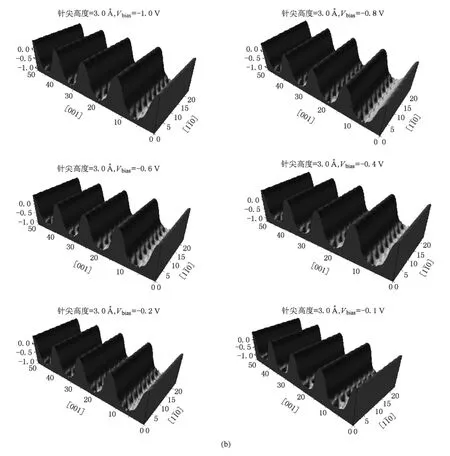
图4 Au(110)-(1×3)缺列再构表面的STM模拟图像 (a)STM形貌图;(b)3.0 针尖高度几种偏压下的线扫

图5 Au(110)-(1×2)针尖高度为5.0 ，Au(110)-(1×3)针尖高度为3.0 时，在不同偏压下的STM扫描时针尖起伏和偏压的关系

在上面的表格中，我们发现氧覆盖度1.0 ML时的LB(1×1)位置有些异常，故研究了氧覆盖为1.0 ML时，Au(110)-(1×1)表面的Au-O间距和原子位置弛豫情况(见表4).观察表中数据可以发现，在LB(1×1)位置，氧原子会进入到最表层和次表层之间，造成 Δd12/d0急剧膨胀，达到了 +46.6%(未吸附前，Δd12/d0=－12.5%)，这主要由于氧原子和金属层之间的排斥作用造成的(见图7)，也是使吸附能值出现异常的原因.

表2 Au(110)-(1×2)和Au(110)-(1×3)缺列再构表面的缺列深度，hij表示从表面算起的第i和j层Au(110)面间距离

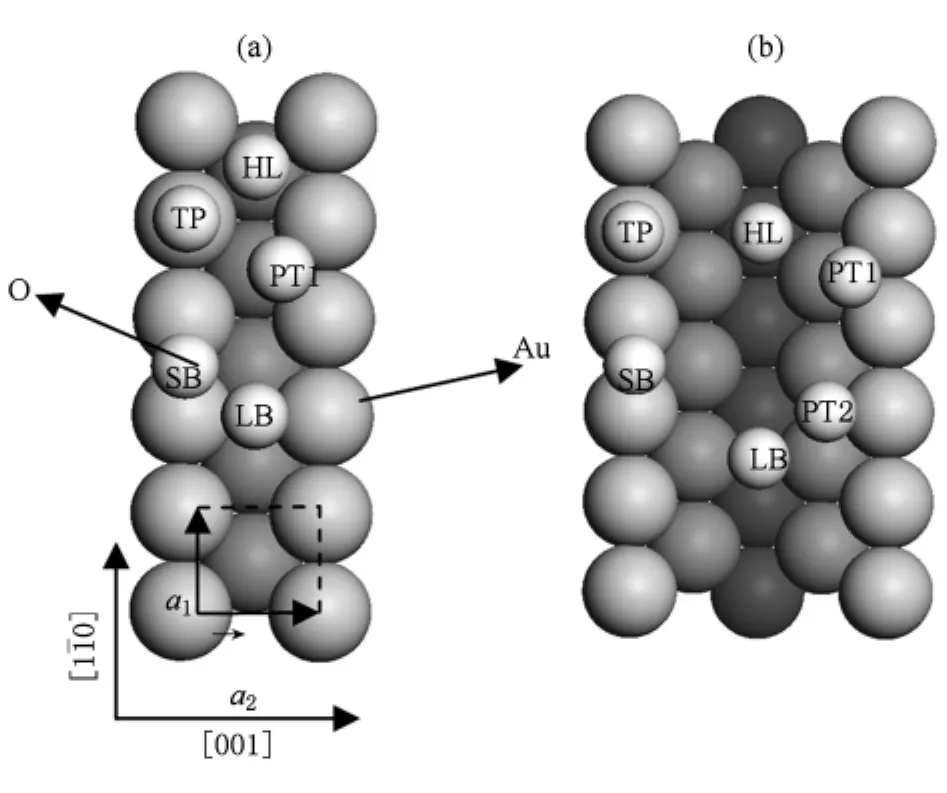
图6 (a)Au(110)-(1×1)表面氧吸附位置;(b)Au(110)-(1×2)缺列再构表面氧吸附位置

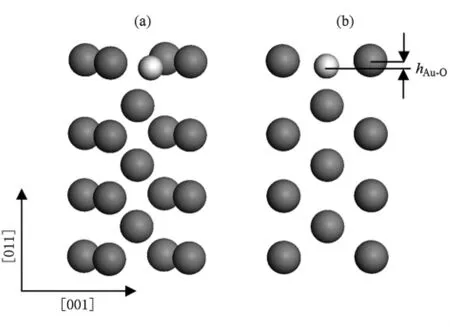
图7 在 LB(1×1)位置，氧吸附 Au(110)面的原子结构示意图 (a)为正面图;(b)为侧面图

表3 Au(110)-(1×1)表面(1.0 ML，0.5 ML)各位置的吸附能;Au(110)-(1×2)(0.5 ML)缺列再构表面各位置的吸附能

表4 氧覆盖度为1.0 ML时，Au(110)-(1×1)表面的Au-O间距和弛豫情况，hAu-O为吸附氧原子和第一层Au(110)面间的距离

4.结 论

用密度泛函理论和第一性原理总能计算研究了Au(110)表面p(1×2)和p(1×3)缺列再构的表面弛豫，表面能，功函数以及STM模拟图像;并且讨论了p(1×1)和 p(1×2)结构氧原子吸附问题.主要结果和结论如下:

1.Au(110)-(1×2)的外层表面间的弛豫分别是 －15.0%(Δd12/d0)和 －1.1%(Δd23/d0)，表面能σrelaxed=52.7 meV/2，功函数 Φ =5.00 eV;相应的，Au(110)-(1×3)的 Δd12/d0= －20.5%，Δd23/d0=+2.7% ，σrelaxed=53.4 meV/2，Φ =4.98 eV.

2.分别在不同偏压和针尖高度下，计算得到了Au(110)-(1×2)和(1×3)缺列再构表面的STM模拟图像，并且获得了恒流模式下的STM针尖起伏高度变化的模拟数据.模拟计算表明，STM图像中显示亮斑带状条纹和暗条纹彼此间隔排列，这是由于［1］方向的原子的缺失.由 Au(110)-(1×2)和Au(110)-(1×3)缺列再构表面的缺列深度比 STM扫描的针尖起伏都大些.

3.研究了Au(110)-(1×1)和(1×2)表面上，五个吸附位置:短桥位(short bridge，SB)，长桥位(long bridge，LB)，顶位(top，TP)，谷位(hollow，HL)，赝三度对称位(pseudo-threefold，PT)的氧吸附情况.在高氧覆盖度下，各吸附位的吸附能值均为负值，吸附过程可视为为吸热过程.我们推测，在低氧覆盖度下，在PT1位置，可能会出现正的吸附能值，发生吸附是吸热过程.在比较各位置的吸附能值时，发现LB(1×1)(氧覆盖度为1.0 ML)位置的吸附能值异常，研究弛豫情况及氧原子和第一层Au(110)面间的距离时，发现氧原子进入到最表层和次表层之间导致.所有的吸附能(以氧分子为参考点)都是负值，说明氧原子在 Au(110)表面的吸附是不可能自发发生的，Au(110)表面对于氧的吸附具有很高的化学惰性.

本研究所包含的部分科学计算在浙江大学物理系物理实验中心的计算集群上进行，特此致谢.

［1］ Hutchings G J 1996 Gold Bull.29 123

［2］ Hutchings G J 2002 Catal.Today.72 11

［3］ Haruta M，Kobayashi T，Sano H，Yamada N 1987 Chem.Lett.16 405

［4］ Haruta M，Tsubota S，Kobayashi T，Kageyama H，Genet M J，Delmon B 1993 J.Catal.144 175

［5］ Sault A G，Madix R J，Campbell C T 1986 Surf.Sci.169 347

［6］ Canning N D S，Outka D，Madix R J 1984 Surf.Sci.141 240

［7］ Gottfried J M，Elghobashi N，Schroeder S L M，Christmann K 2003 Surf.Sci.523 89

［8］ Linsmeier Ch，Wanner J 2000 Surf.Sci.454-456 305

［9］ Gottfried J M，Schmidt K J，Schroeder S L M，Christmann K 2002 Surf.Sci.511 65

［10］ Gottfried J M，Schmidt K J，Schroeder S L M，Christmann K 2003 Surf.Sci.525 184

［11］ Gottfried J M，Schmidt K J，Schroeder S L M，Christmann K2 003 Surf.Sci.525 197

［12］ Sturmat M，Koch R，Rieder K H 1996 Phys.Rev.Lett.77 5071

［13］ Koch R，Sturmat M，Schulz J J 2000 Surf.Sci.454-456 543

［14］ Moritz W，Wolf D 1979 Surf.Sci.88 L29

［15］ Bining G，Rohrer H，Gerber Ch，Weibel E 1983 Surf.Sci.131 L379

［16］ Gritsch T，Coulman D，Behm R J，Ertl G 1991 Surf.Sci.527 297

［17］ Olivier S，Tréglia G，Saúl A，Willaime F 2006 Surf.Sci.600 5131

［18］ Pyykk P 1988 Chem Rev.88 563

［19］ Pyykk P 2004 Angew.Chem.116 4512

［20］ Smit R H M，Untiedt C，Yanson A I，van Ruitenbeek J M 2001 Phys.Rev.Lett.87 266102

［21］ Thijssen W H A，Strange M，aan de Brugh J M J，van Ruitenbeek J M 2008 New J.Phys.10 033005

［22］ Landmann M，Rauls E，Schmidt W G 2009 Phys.Rev.B 79 045412

［23］ Landmann M，Rauls E，Schmidt W G 2009 J.Phys.Chem.C 113 5690

［24］ Perdew J P，Burke K，Ernzerhof M 1996 Phys.Rev.Lett.77 3865

［25］ Kresse G，Furthermüller J 1996 Comput.Mater.Sci.6 15 Kresse G，Furthermüller J 1996 Phys.Rev.B 55 11196

［26］ Vanderbilt D 1994 Phys.Rev.B 41 7892

［27］ Bl chl P E 1994 Phys.Rev.B 50 17953

［28］ Huang G Y，Wang C Y，Wang J T 2010 Chin.Phys.B 19 013101

［29］ Kresse G，Joubert J 1999 Phys.Rev.B 59 1758

［30］ Chiarotti G 1993 in Physics of Solid Surfaces-Structure，Landolt-B rnstein-GroupⅢ Condensed Matter(Vol.24a)(New York:Springer)

［31］ Monkhorst H J，Pack J D 1976 Phys.Rev.B 13 5188

［32］ Payne M C，Teter M P，Allan D C，Arias A，Joannopoulos J D 1992 Rev.Mod.Phys.64 1045

［33］ Huber K P，Herzberg G 1997 Constants of Diatomic Molecules，Molecular Spectra and Molecular Structure(Vol.Ⅳ)(New York:Van Nostrand Reinhold)

［34］ Stull D R，Prophet H 1971 JANAF Thermochemical Tables，2nd ed.

［35］ Fasolino A，Selloni A，Shkrebtii A 1993 in Landolt-B rnstein-GroupⅢ Condensed Matter，Physics ofSolid Surfaces-Structure(Vol.24a)(New York:Springer)

［36］ Moeller J，Snowdon K J，Heiland W 1986 Surf.Sci.178 475

［37］ Copel M，Gustafsson T 1986 Phys.Rev.Lett.57 723

［38］ Moritz W，Wolf D 1985 Surf.Sci.163 L655

［39］ Vlieg E，Robinson I K，Kern K 1990 Surf.Sci.233 248

［40］ Haberle P，Fenter P，Gustafsson T 1989 Phys.Rev.B 39 5810

［41］ Tersoff J，Hamann D R 1983 Phys.Rev.Lett.50 1998

［42］ Chen C J 1993 Introduction to Scanning Tunneling Microscopy(Oxford:Oxford University Press)

［43］ Tao X M，Tan M Q，Zhao X X，Chen W B，Chen X，Shang X F 2006 Surf.Sci.600 3419

［44］ Chen W B，Tao X M，Chen X，Tan M Q 2008 Acta.Phys.Sin.57 488(in Chinese)［陈文斌、陶向明、陈 鑫、谭明秋 2008物理学报57 488］

［45］ Cai J Q，Tao X M，Chen W B，Zhao X X，Tan M Q 2005 Acta Phys.Sin 54 5350(in Chinese)［蔡建秋、陶向明、陈文斌、赵新新、谭明秋 2005物理学报 54 5350］

［46］ Kaghazchi P，Jacob T 2007 Phys.Rev.B 76 245425

Density-functional theory investigation of atomic geometry and oxygen adsorption of Au(110)surface*

Wang Mang-Mang Ning Hua Tao Xiang-Ming Tan Ming-Qiu
(Department of Physics，Zhejiang University，Hangzhou 310027，China)(Received 18 April 2010;revised manuscript received 24 June 2010)

We have performed density-functional theory calculations of the atomic structure and the oxygen adsorption properties of Au(110)surfaces.The relaxations of missing-row reconstructed Au(110)-(1×2)surface are calculated to be－15.0%(Δd12/d0)and －1.1%(Δd23/d0).The relevant surface energy and workfunction are calculated to be 52.7 meV/2and 5.00 eV，respectively.In the case of missing-row reconstructed Au(110)-(1×3)surface the surface atomic relaxations are calculated to be －20.5%(Δd12/d0)and+2.7%(Δd23/d0)which are quite differente from those of Au(110)-(1 ×2).However，in the later case，the surface energy and workfunction are found to be very close to those of missing-row reconstructed Au(110)-(1 ×2)surface，i.e.，53.4 meV/2and 4.98 eV.We have simulated the scanning tunneling microscope(STM)images of both reconstructed surfaces and found that the missing row exhibits a remarkable hollow in the STM morphology.The further calculation of oxygen adsorption on both surfaces reveals that the adsorption energies in these cases are negative.These results indicate that the Au(110)surface is free from oxygen adsorption and reaction，showing highly chemical inertia.

missing-row reconstructed Au(110)surface，STM image，oxygen adsorption

.E-mail:mqtan@zju.edu.cn

*浙江省教育厅科研项目(批准号:Y200804278)资助的课题.

.E-mail:mqtan@zju.edu.cn

*Project supported by the Research Projects of Department of Education of Zhejiang Province(Grant No.Y200804278).

PACS:73.20.－ r，68.35.－ p，68.37.Ef，68.43.Fg