基于市场细分的两周期闭环供应链定价策略
2011-10-24达庆利
孙 浩,达庆利
(1.青岛大学 国际商学院,山东 青岛 266071;2.东南大学 经济管理学院,南京 211189)
基于市场细分的两周期闭环供应链定价策略
孙 浩1,达庆利2
(1.青岛大学 国际商学院,山东 青岛 266071;2.东南大学 经济管理学院,南京 211189)
文章建立了基于市场细分的两周期再制造闭环供应链的决策模型,得出了制造商的最优批发价格和回购价格、零售商对新产品和再制造产品的差异定价以及双方的利润,并分析了不同参数变化对于价格、回收率和利润的影响。通过算例验证了所得结论的正确性。
闭环供应链;市场细分;回收;再制造计
0 引言
逆向物流是近年来物流领域研究的热点之一。制造商通过对废旧产品的回收再制造,不仅可以减少污染,保护环境,而且可以获取额外的利润。如柯达制造的再生循环照相机、惠普生产的可重复填充利用的打印机墨盒,已为其带来可观的经济效益。逆向物流的产生使供应链结构从单一的传统正向供应链发展为包括逆向供应链在内的闭环供应链系统。而在闭环供应链中,制造商如何有效地引导回收商或零售商回收废旧产品以及如何制定相应的回收和回购价格、协调成员间的利润分配是其中重要的决策问题。
检索国内外相关研究发现,这些文献均假设制造商集所有的物流活动于一身,从系统整体的角度来研究最优的生产计划、回收再制造计划与产品定价的联合决策,鲜有文献将其扩展至分散式闭环供应链中。葛静燕从社会环保意识、新产品和再制造产品差异定价的角度比较了两种分散式回收模式(制造商回收和零售商回收)下的最优决策,并分析了社会环保意识对产品销量及双方利润的影响,但其只探讨了单周期、回收率为常数的情况。孙浩将模型推广至两周期环境中,研究在分散式决策下制造商的最优批发价格和回购价格、零售商对两种产品的差异定价、回收率以及双方的利润,并分析不同参数变化对于均衡解的影响,但其假设再制造产品在二手市场销售,而本文讨论的是两种产品同时在原市场销售、二者形成市场细分的情形。
1 问题描述与假设条件
1.1 问题描述
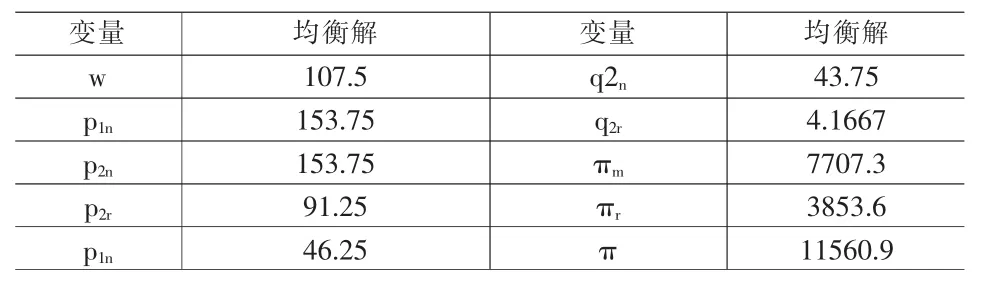
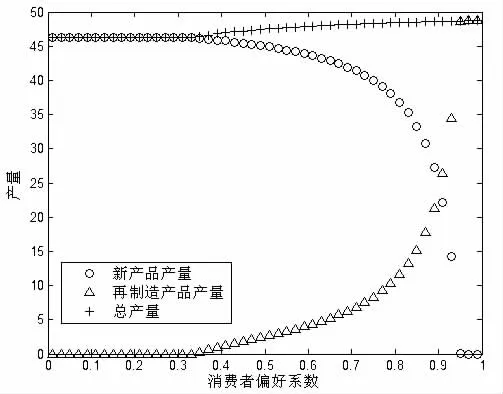
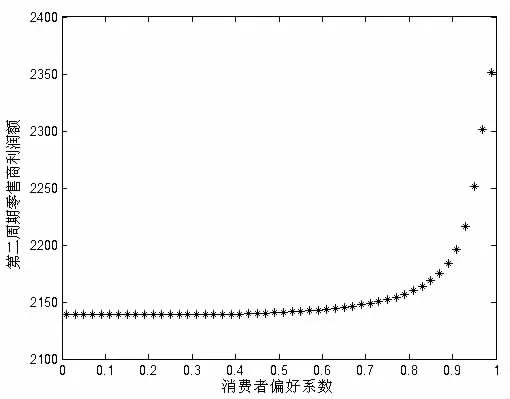
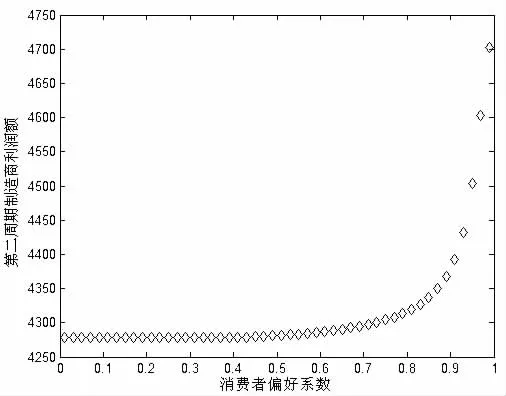
考虑如图1所示的零售商回收模式下两周期再制造闭环供应链。第一周期:零售商以价格w从制造商处批发新产品,以价格p1n销售给消费者(新产品销量为q1n),并在产品生命周期结束后从消费者处回收部分EOL产品,回收率为θ;第二周期:制造商以价格向零售商回购EOL产品,同时进行新产品的生产和EOL产品的再制造 (单位成本分别为cn和cr,cr 为了更清楚地阐述模型,作出如下假设: (1)只研究单一制造商和单一零售商的情况,且二者均为风险中性且完全信息。 (2)制造商是Stackelberg领导者,他对零售商有足够的渠道影响力。 (3)假设零售商已经构建了合适的回收物流网络,单位回收费用忽略不计,且第一周期零售商回收的EOL产品在第二周期均被制造商实施再制造。 (4)第一周期新产品的需求函数为,其中为市场容量。在第二周期,根据消费者效用理论,假设消费者对再制造产品的估价是对新产品估价的δ倍,即δ为消费者对再制造产品的偏好系数,且0<δ<1,则在市场细分情形下两种产品的需求量与价格之间的关系为: 上式表明新产品和再制造产品的需求量均随自身零售价的增加而减少,随对方零售价的增加而增加,即两种产品表现出一定的替代性。另外,随着消费者对再制造产品偏好系数的增加,再制造产品的需求量增加,新产品的需求量减少。 (5)考虑利润的时间价值,用ρ表示第二周期利润的时间折现率,其中ρ∈(0,1]。 (6)λw为再制造产品的批发价,其中参数 λ∈(0,1],其大小由再制造产品的质量、双方的讨价还价能力等多方面因素决定。 由于本文主要研究新产品与再制造产品如何进行市场细分及相应的定价、产量决策,所以首先考虑当消费者偏好系数时的情形,通过计算给出其均衡解及参数δ的取值范围,进而讨论当市场中分别只有新产品和再制造产品的情况。 (1)市场上同时存在新产品与再制造产品 由于制造商是Stackelberg领导者,因此决策顺序如下:在制造商首先确定批发价格w和回购价格b后,零售商根据制造商的决策确定价格p1n、p2n、p2r及回收率θ,该问题可采用逆向归纳法求解。另外由于零售商的决策是多周期动态规划问题,因此同样采用回溯法:首先假定第一周期的p1n确定,求解第二周期的最优定价p2n与p2r、及回收率θ,然后再代入第一周期的利润函数中求解p1n。 将式(1)代入(4),分别对 p2n,p2r求二阶偏导数,结果如下: 将以上反应函数代入式(3)的零售商利润中,对求一阶导数得到 再将式(9-11)代入制造商的利润函数中 分别对πM(w,b)求w,b的一阶和二阶偏导数: 所以πM是w和b的联合凹函数,其最优解对应于一阶导数的零点: 进而可求出 π*和 π*。 MR显然,由于≤(即 0≤θ*≤1),应满足式(25)的约束。 另外,要使市场上两种产品同时存在的假设成立,需满足式 (1)的约束,δ的取值必须限定于以下范围: 同理可推出只有新产品和只有再制造产品时δ需满足的条件,进而可求出两种情形下制造商、零售商的利润及系统总利润。 (2)只有新产品,δ∈(0,cr]cn 根据以上均衡解的表达式,可以得到以下结论: 性质1 新产品批发价格w*与参数ρ、λ和δ的取值均无关,再制造产品的转移价格b*与λ和δ的取值相关。另外两周期新产品的价格和相同。 证明:从相关价格变量均衡解的表达式可以看出。 本节首先给出参数值确定时两周期闭环供应链中决策变量的均衡解,然后通过仿真分析第二周期制造商和零售商的销量、利润随消费者偏好系数δ的变化规律。在满足式(25)的约束下取参数 准n=200,cn=15,cr=5,ρ=0.8,λ=0.8,δ=0.6。 表1 价格及利润变量的均衡解 从图1可以看出:在δ∈(0,0.333)部分,市场中只有新产品(可计算 cr/cn=0.333);当 δ∈[0.333,0.95),市场中既有新产品,也有再制造产品(可计算 1-(cn-cr)/准n=0.95);当 δ∈[0.95,1)时,市场中只有再制造产品。而且随δ的增加而减小,及总销量均随δ的增大而增大。这也验证了性质2的正确性。 图1 第二周期、及总销量随消费者偏好系数的变化情况 从图2和图3可以看出:在δ∈(0,0.333)部分,由于市场中只有新产品,及均与偏好系数δ无关;在δ∈[0,1部分,无论是两种产品都存在还是只存在再制造产品,及均随δ∈的增大而增大。这也验证了性质3的正确性。 图2 第二周期零售商利润随δ的变化情况 图3 第二周期制造商利润随δ的变化情况 本文建立了基于市场细分的两周期再制造闭环供应链决策模型,得出了制造商的最优批发价格和回购价格、零售商对新产品和再制造产品的差异定价以及双方的利润,并分析了不同参数变化对于价格、回收率和利润的影响。得到如下结论: (1)制造商对新产品的批发价格与参数ρ、λ及δ的取值均无关,而再制造产品的转移价格与λ和δ相关,且第一周期与第二周期新产品的销售价格相同。 (2)第二周期新产品的销量随着消费者偏好程度δ的增加而减小,再制造产品的销量及总销量均随δ的增大而增大。 (3)第二周期利润零售商和制造商的利润均随消费者偏好系数δ的增大而增大。 未来的研究是将本文的两周期模型扩展至多周期环境中,以及探讨需求不确定性对渠道成员最优决策的影响。 [1]Lebreton B.Strategic Closed-loop Supply Chain Management[M].Berlin,Heidelberg:Springer-verlag,2007. [2]Savaskan R C,Bhattacharya S,Wassenhove L N V.Closed-loop Supply Chain Models with Product Remanufacturing[J].Management Science,2004,50(2). [3]Savaskan R C,Wassenhove L N V.Reverse Channel Design:The Case of Competing Retailers[J].Management Science,2006,52(1). [4]黄祖庆,达庆利.直线型再制造供应链决策结构的效率分析[J].管理科学学报,2006,9(4). [5]Kerr W,Ryan C.Eco-efficiency Gains from Remanufacturing.A Case Study of Photocopier Remanufacturing at Fuji Xerox Australia[J].Journal of Cleaner Production,2001,9(1). [6]Lebreton B.Strategic Closed-loop Supply Chain Management[M].Berlin,Heidelberg:Springer-verlag,2007. [7]Bakal I,Akcali E.Effects of Random Yield in Reverse Supply Chains with Price-sensitive Supply and Demand[J].Production&Operations Management,2006,15(3). [8]Atasu A,Sarvary M,Van Wassenhove L N.Remanufacturing as a Marketing Strategy[J].Management Science,2008,54(10). [9]Heese H S,Cattani K,Ferrer G,et al.Competitive Advantage through Take-back of Used Products[J].European Journal of Operational Research,2005,164(1). [10]Ferguson M E,Toktay L B.The Effect of Competition on Recovery Management[J].Production and Operations Management,2006,15(3). [11]Mitra S,Webster S.Competition in Remanufacturing and the Effects of Government Subsidies[J].International Journal of Production Economics,2008,111(2). [12]Webster S,Mitra S.Competitive Strategy in Remanufacturing and the Impact of Take-back Laws[J].European Journal of Operational Research,2007,25(6). [13]Debo L G,Toktay L B,Van Wassenhove L N.Market Segmentation and Product Technology Selection for Remanufacturable Products[J].Management Science,2005,51(8). [14]徐峰,盛昭瀚,陈国华.基于异质性消费群体的再制造产品的定价策略研究[J].中国管理科学,2008,16(6). [15]葛静燕,黄培清,李娟.社会环保意识和闭环供应链定价策略研究——基于纵向差异模型的研究[J].工业工程与管理,2007,12(4). [16]孙浩,达庆利.基于产品差异的再制造闭环供应链定价与协调研究[J].管理学报,2010,7(5). [17]Bhattacharya S,Guide V D R,Wassenhove L N V.Optimal Order Quantities with Remanufacturing Across New Product Generations[J].Production and Operations Management,2006,15(3). F252 A 1002-6487(2011)04-0173-04 国家自然科学基金资助项目(70772059;70472033) 孙 浩(1981-),男,山东青岛人,博士研究生,讲师,研究方向:逆向供应链管理。达庆利(1945-),男,江苏南京人,教授,博士生导师,研究方向:逆向供应链管理等。 (责任编辑/易永生)1.2 模型假设
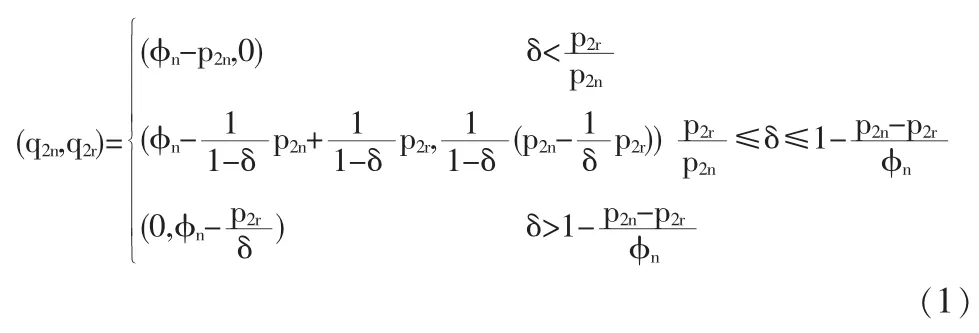
2 基于市场细分的两周期再制造闭环供应链决策模型
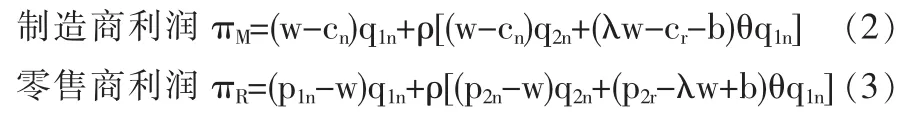
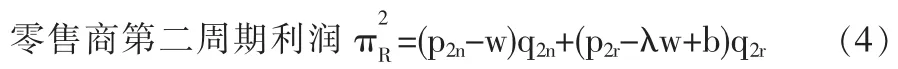


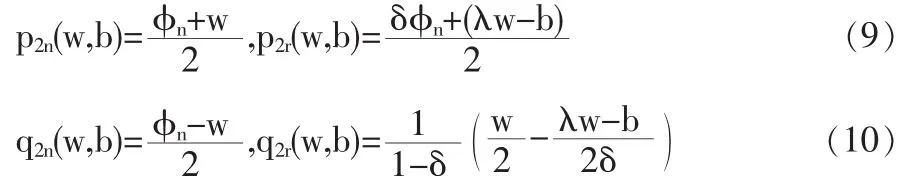
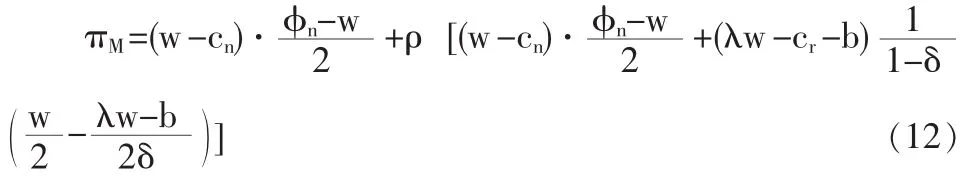

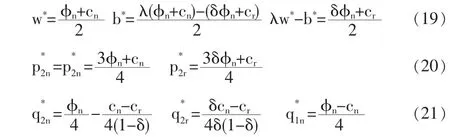



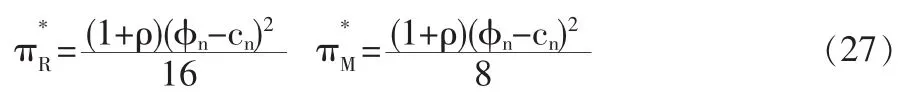
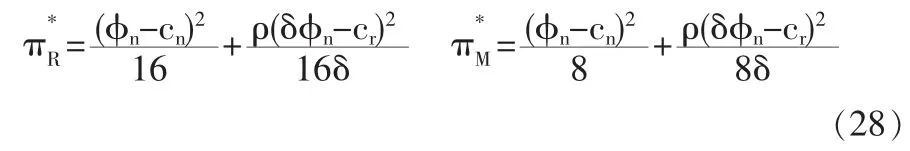
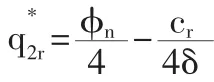
3 算例分析
4 结论
