基于函数型数据分析的数据挖掘功能研究

王凯平

（山东大学 管理学院，济南 250100)

基于函数型数据分析的数据挖掘功能研究

王凯平

（山东大学 管理学院，济南 250100)

数据挖掘功能是数据挖掘研究与应用的一个重要方面。数据挖掘功能用于指定数据挖掘任务中要找的模式类型。当前，数据挖掘的功能所处理的主要是传统的数据，对于函数型数据的研究还不是很多。文章探讨了数据挖掘中可以挖掘的几种函数型数据模式，包括数据描述、分类、聚类和回归。

函数型数据；数据挖掘；模式

0 引言

近年来，数据挖掘的研究与应用引起了统计学、计算机科学、管理学、金融学等学术领域以及众多知名企业的广泛关注。数据挖掘在功能模式、方法、应用领域和软件开发等各个方面都得到了广泛的研究。数据挖掘研究与应用的一个重要方面就是关于数据挖掘功能的研究。数据挖掘功能用于指定数据挖掘任务中要找的模式类型。数据挖掘的任务一般可以分为两类[1]：描述和预测。描述性任务刻划数据库中数据的一般特性。预测性任务在当前数据上进行推断，以进行预测。运用各式理论技术，数据挖掘可以建立的模式包括数据描述、分类、聚类、回归等[2]。

当前，数据挖掘的功能所处理的主要是传统的数据，即把数据作为离散的数据点来看待，这能够满足很多应用领域的需要。然而，随着社会的进步和科学技术的发展，有些领域中出现了一种新的数据——函数型数据。当观测的时间点十分密集时，这些数据就会呈现出一种函数特征。函数型数据是一系列的曲线或形状对象，更一般地，是一系列的函数型数据值。例如，在线拍卖数据是函数型数据的一个典型代表。在线拍卖不是传统拍卖在Internet上的简单移植，它在商务模式、买卖双方行为特征和拍卖方式等方面都有自身独特的性质，从而使得在线拍卖数据与传统的数据相比具有很大的区别。文献[3]详细分析了在线拍卖数据的函数型数据特点。

本文探讨了数据挖掘功能中可以挖掘的几种函数型数据模式，包括数据描述、分类、聚类和回归。

1 基于传统数据的数据挖掘功能模式

1.1 数据描述

数据描述的目的是对数据进行概括，以给出它的总体特征。最简单的数据描述方法是利用统计学中的方法，计算出数据库中各个数据项的总和、平均值、方差等。

1.2 分类

分类是找出描述并区分数据类别的模型（或函数），以便能够使用该模型（或函数）来确定未知类型的对象所属的类别。

目前对于传统数据的分类技术有很多种，例如Bayes分类、决策树分类、神经网络分类、k－最临近分类、遗传算法分类、粗集分类等等，不同的分类方法适用于不同特点的数据。下面介绍一下贝叶斯分类。

令q-维向量X代表一个观测对象，它来自于多个类中的某一个。假设第i个类的密度为fi(x)，先验概率为πi。由Bayes公式，有后验概率

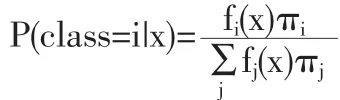
Bayes分类将X归于具有最高后验概率的那个类。如果我们进一步假设第i个类具有正态分布，其均值为μi，协方差阵为∑，则可以证明以上Bayes分类等价于按下述线性判别函数进行分类[4]

其中，

1.3 聚类

聚类是指按被处理对象的特征分类，将有相同特征的对象归为一类，其目的是将类间的差异找出来，同时也将类内成员的相似性找出来。例如，对在一个商场购买力较大的顾客居住地进行聚类分析，以帮助商场针对相应顾客群采取有针对性的营销策略。其与分类的区别在于聚类前并不知道会以何种方式或根据来分类。

目前的聚类算法大体上可以划分为以下几类[5]：层次的方法、划分的方法、基于密度的方法、基于网格的方法以及基于模型的方法等。

基于模型的方法为每一类假定了一个模型,寻找数据对给定模型的最佳拟合。假定观测xi,…xn来自于具有G个分量组成的混合分布。令fk(x|θk)为第k个类的密度，θk为参数，再令zi=(zi1,…,ziG)为第i个观测的类成员向量，其中

所有的zi都是未知的，一般通过两种方式处理：分类似然法和混合似然法。

(1)分类似然法

该方法将zi看作参数，模型通过最大化如下似然函数来拟合：

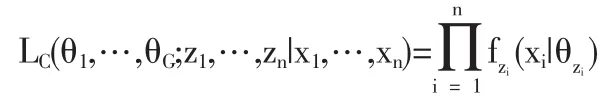
(2)混合似然法

该方法将看作是具有参数(π1,…,πG)的多项分布，其中 πk为观测属于第k个类的概率。参数由最大化下式来估计：

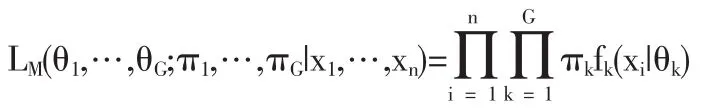
1.4 回归

回归是研究因变量与一系列的自变量之间相关关系的一个有力工具。确定了因变量与自变量的关系后，就可以通过回归模型根据自变量的观测值预测因变量的值。回归有三种类型：参数回归（包括线性回归和非线性回归）、非参数回归和半参数回归[6]。

(1)参数回归

参数回归包括线性回归（一元和多元线性回归）和非线性回归（如广义线性模型）。参数回归应用最为广泛，其原因在于：第一，对于某领域的专业人员来说，一个模型的参数经常会有重要的实际含义；第二个原因在于其统计上的简单性——对于整个函数的估计归结为推断几个参数值；第三个原因在于，如果参数假设是正确的，那么参数回归非常有效。

(2)非参数回归

非参数回归具有很大的灵活性，它并不对真实模型作结构方面的假设，或者说，它不假设真实模型可以被有限维参数所控制。非参数回归在降低模型偏差方面非常灵活，然而，在多变量情况下，由于维数问题的影响，它对真实函数的估计达不到合理的准确度。

(3)半参数回归

在参数回归和完全的非参数回归之间有许多可能的选择。最为典型的就是假设所估计的函数具有某种形式（如可加形式），然而这种形式并不同于完全的参数结构。由此产生的模型我们称为半参数回归模型。与参数回归相比，这种半参数模型能够降低模型错误所导致的偏差；而与非参数回归相比，它又比完全的非参模型要小的多，从而对于未知参数及函数的估计能够达到合理的准确度。典型的半参数模型，包括可加模型、部分线性模型及其推广模型。

2 基于函数型数据的数据挖掘功能模式

函数型数据分析的研究对象是一系列的函数型观测值x(t)。近年来，许多传统的统计方法被推广到了函数型数据的场合，具体可参见文献[7]。然而，在数据挖掘领域，对于函数型数据的研究还不是很多。本文从数据挖掘的功能出发，探讨了数据挖掘中可以挖掘的几种函数型数据模式，包括数据描述、分类、聚类和回归。

2.1 函数型数据描述

传统的描述统计量同样适用于函数型数据。例如，函数型数据的均值函数可以表示为，而方差函数为

2.2 函数型数据分类

由于函数型数据是无穷维的，因此，传统的基于有限维数据的分类方法不能直接应用于函数型数据。

令g(t)为从第i个类中随机抽取的个体曲线。假设如果g(t)属于第i个类，则其分布为如下的Gauss过程：

由于随机因素的影响，我们在不同的时间点t1,…,tn对于函数曲线的观测向量Y是有误差的，假设误差不相关，且均值为0，方差为σ2。则Y的分布为

N(μI,Ω+σ2I)，其中

可以将 μi和∑=Ω+σ2I代入（2）式得到 Bayes分类。 现有的函数型数据分类方法就是通过估计μi(t)和ω(t,t')，然后将其估计值代入（1）中进行分类。其估计方法通常有两种[4]：正则化方法和滤波方法。例如，滤波方法是使用基函数来估计μi(t)和 ω(t,t')。

2.3 函数型数据聚类

基于模型的函数型数据聚类方法与分类方法有共通之处。 对于曲线 g(t)，有（2）、（3）两式，函数型数据聚类就是首先估计μi(t)和ω(t,t')，然后根据其估计值进行聚类。以μi(t)为例，常用的滤波方法是使用基函数 准(t)=(准1(t),…,准p(t))来估计 g(t)，即g(t)=准(t)η，使用最小二乘法分别估计每条曲线的系数向量η，然后使用基于有限维数据的聚类方法对估计的系数向量进行聚类，所产生的聚类均值乘以准(t)后就得到了μi(t)的估计。ω(t,t')的估计与此类似。详细的聚类过程可参见文献[8]。

分层的聚类方法可参见文献[9]。

2.4 函数型数据回归

与传统的回归类似，函数型数据回归也分为参数、非参数和半参数三种形式。

(1)参数形式

参数形式的函数型数据回归分为线性和非线性两种情况，文献[10]考虑了函数型数据的广义线性模型，将线性回归与非线性回归统一在一个模型中进行研究，并给出了具体的估计方法。

(2)非参数和半参数形式

关于非参数和半参数形式的函数型数据回归是目前研究的一个热点领域，具体可参见文献[11,12]。

3 总结

当前，数据挖掘对于传统数据的各种功能模式已经得到了相当广泛的研究和应用，而对于函数型数据的研究还处于起步阶段。其原因在于，就函数型数据分析自身来讲，其研究时间并不长，很多问题并没得到完善的解决。

然而，许多学科其大量的方法和思想都来源于现实的需求。随着数据挖掘在各行各业的广泛应用，必然会越来越多的处理函数型数据、挖掘函数型数据的各种模式。这反过来也会促进函数型数据分析的不断深入和完善。

[1]J.W.Han,M.Kamber.Data Mining:Concepts and Techniques[M].Sinagpore:Elsevier,2006.

[2]朱世武,崔嵬,张尧庭,谢邦昌.数据挖掘运用的理论与技术[J].统计研究,2003,(8).

[3]Jank W,Shmueli G.Functional Data Analysis in Electronic Commerce Research[J].Statistical Science,2006,21(2).

[4]James G M,Hastie T J.Functional Linear Discriminant Analysis for Irregularly Sampled Curves[J].Journal of the Royal Statistical Society,Series B(Statistical Methodology),2001,63(3).

[5]中国人民大学统计系数据挖掘中心.数据挖掘中的聚类分析[J].统计与信息论坛,2002,17(3).

[6]Hürdle W,Müller M,Sperlich S,Werwatz A.Nonparametric and Semiparametric Models[M].Heidelberg:Springer Verlag,2004，(3).

[7]Valderrama M J.An Overview to Modelling Functional Data[J].Computational Statistics,2007,22(3).

[8]James G M,Catherine A.Clustering for Sparsely Sampled Functional[J].Journal of the American Statistical Association,2003，98(462).

[9]Ferreira L,Hitchcock D B.A Comparison of Hierarchical Methods for Clustering Functional Data[J].Communications in Statistics-Simulation and Computation,2009,38(9).

[10]James G M.Generalized Linear Models with Functional Predictors[J].Journal of the Royal Statistical Society,Series B (Statistical Methodology),2002,64(3).

[11]Ferraty F,Mas A,Vieu P.Nonparametric Regression on Functional Data:Inference and Practical Aspects[J].Australian&New Zealand Journal of Statistics,2007,49(3).

[12]Dabo-Niang S,Guillas S.Functional Semiparametric Partially Linear Model with Autoregressive Errors[J].Journal of Multivariate Analysis,2010,101(SI).

O212.4

A

1002－6487（2011）04－0160-02

山东省软科学研究计划项目（2009RKA036）；山东大学自主创新基金资助项目(2010TS073)

王凯平（1975-)，男，山东人，博士，讲师，研究方向：数据挖掘。

（责任编辑/易永生）