寿命产品可靠度的贝叶斯估计

徐 宝

(1.吉林师范大学 数学学院，吉林四平 136000；2.吉林大学 数学研究所，长春 130012)

寿命产品可靠度的贝叶斯估计

徐 宝1，2

(1.吉林师范大学 数学学院，吉林四平 136000；2.吉林大学 数学研究所，长春 130012)

在与信息论中的熵函数有关的一种新的加权对称熵损失函数下，用参数估计方法研究了寿命服从几何分布的产品可靠度的估计问题。得到了可靠度的贝叶斯估计的一般形式与精确形式并讨论了贝叶斯估计的可容许性。最后研究了可靠度的多层贝叶斯估计，数值算例表明研究结果能为实际生产提供稳健性较高的估计形式。

可靠度；贝叶斯估计；多层贝叶斯估计；稳健性

1 问题的提出

在现代实际生产中，许多产品都要求有很高的可靠性指标，因此必须对产品进行可靠性测试。若对产品的测试手段是成败型试验(如脉冲、振荡等冲击试验)，则其寿命是以成败次数来衡量的。在测试产品的寿命的研究中几何分布起着重要的作用。因此，对几何分布的可靠性分析具有理论和实际应用价值。在贝努里试验中，令θ为每次试验成功的概率(也称其为可靠度)，若进行了x+1次试验，前x次成功而第x+1次失败的概率为 P(X=x)=θx(1-θ),0<θ<1,x=0,1,2,…，则称随机变量X服从几何分布G(θ)。几何分布及其均值以及可靠度的贝叶斯估计问题已得到广泛研究[1-6]，本文在这些文献使用的与信息论中的熵函数有关的几种损失函数基础之上，提出一种新的损失函数——加权p，q对称熵损失函数

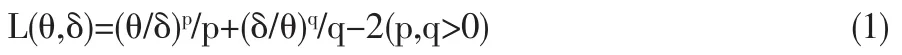
这里δ是待估参数θ的估计量。容易看出损失函数(1)关于待估参数与其估计量是p，q对称的，也就是交换二者以及p，q的位置，不影响损失函数的形式。这个特性是熵损失函数所不具备的，而且当p=q时，损失(1)具有与平方损失函数以及绝对损失函数一样的对称性。在这个损失函数下，本文研究几何分布可靠度θ的贝叶斯估计和多层贝叶斯估计及其性质。

2 可靠度θ的贝叶斯估计

这一部分在贝叶斯框架下，利用损失函数(1)来研究参数θ的估计及其性质。下面定理给出参数θ的贝叶斯估计。

定理 2.1令 X～G(θ)，在损失函数(1)下，对任何先验分布，参数θ的贝叶斯估计为

证明：设δ(X)为参数θ的任一估计，在损失函数(1)下，δ(X) 对应的贝 叶 斯 风 险 为 E[L(θ,δ)]=E{E[L(θ,δ)]|X}=E，上式左端E表示关于θ与样本x的联合分布取期望。欲求θ的贝叶斯解，只须关于δ极小化即可。易知(2)式是其唯一最小值点，从而得到θ的贝叶斯估计为(2)式。

下面考虑在给定先验分布π(θ)后，参数θ的贝叶斯估计精确形式及其性质。

定理2.2若参数θ的先验为贝塔分布Beta(a,1)=aθa-1,a>0为超参数，则在损失函数 (1)下θ的贝叶斯估计为δB(x)=，并且是θ的可容许估计。

证明:易知参数 θ 的后验密度为 h(θ|X)∝θx+a-1(1-θ),于是有

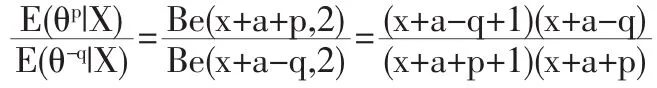
从而 δB(x)=，并且是可容许的。若不然，假设存在另一个估计 δ(x)优于 δB(x)，则必有 δ(x)的贝叶斯风险小于或等于δB(x)的贝叶斯风险，即δ(x)也是一个贝叶斯估计，这与θ的贝叶斯估计唯一性矛盾，从而δ(x)=δB(x)， 故 δB(x)是可容许的。

3 可靠度θ的多层贝叶斯估计

注意到θ的贝叶斯估计的精确形式中含有超参数α，若对超参数再给出一个先验，称之为超先验，由先验和超先验决定的一个新先验就称为多层先验。本文应用文[7]的结果，取超参数 α 的先验 π(a)为 U(1,c)，其中 2≤c≤6，则参数 θ 的多层先验密度为

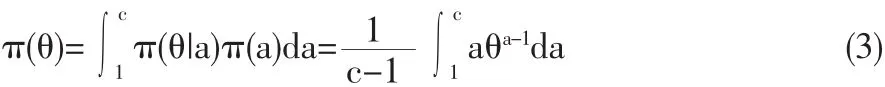
定理3.1在多层先验密度(3)下，几何分布可靠度θ的多层贝叶斯估计为

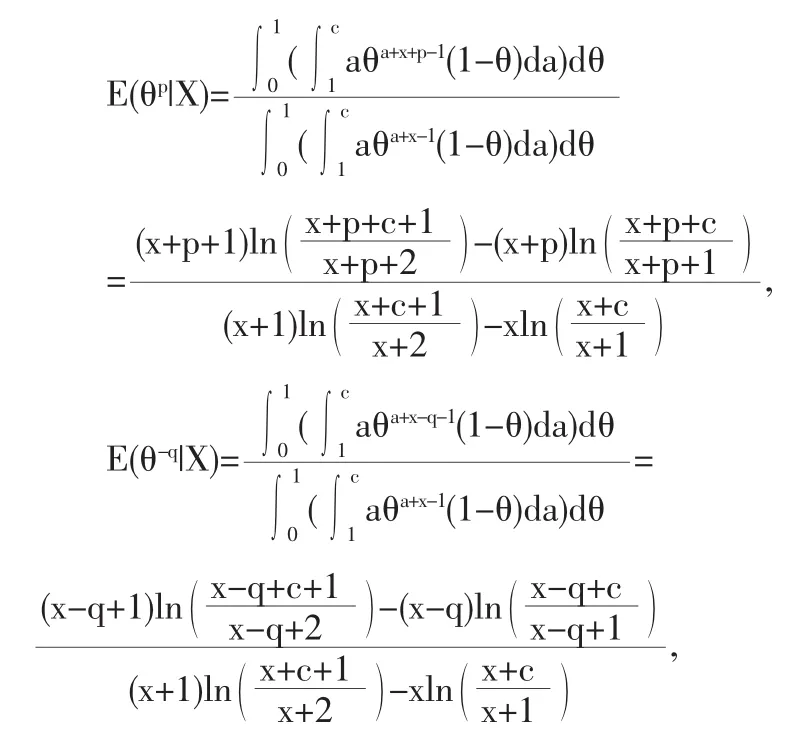
从而θ的多层贝叶斯估计为(4)式。

4 说明与讨论

表1 p=q=1时产品可靠度的多层贝叶斯估计

表2 p=1/2,q=3/2时产品可靠度的多层贝叶斯估计

表3 p=3/2,q=1/2时产品可靠度的多层贝叶斯估计

本文在贝叶斯框架下使用加权p，q对称熵损失函数研究了几何分布可靠度的估计问题，得到了与文[6]相似的估计形势。由于文[6]已经表明可靠度的多层贝叶斯估计稳健，而本文所使用的损失函数又是文[6]所使用的q对称熵损失函数的进一步推广形式，有两个可供调整的常数p与q，因此能更容易得到预期的估计效果。下面应用文[6]中的的数值例子给予说明。

设对某寿命产品进行了两批试验，两批试验数据结果分别为x=19和x=30，对 c(2≤c≤6)，给定 p，q的值来计算几何分布可靠度的多层贝叶斯估计，限定p+q=2，分别计算了(1)p=q=1，(2)p=1/2，q=3/2，(3)p=3/2，q=1/2 三种情形下几何分布可靠度的多层贝叶斯估计，结果由表1、表2、表3给出。

其中表1的结果与文[6]的结果一致。从上述三个表中可以看出随着产品可靠性的提高，其可靠度的估计的极差越小，估计越稳健，而且选择合适的p，q值可以得到更稳健的估计。

[1]Chen L S.Selecting the Best Geometric Distribution Based on Type-ICensored Data:a Bayesian Approach[J].Journal of Statistical Planning and Inference,2010,140.

[2]Anna D.Records from Geometric Distribution[J].Statistics and Probability Letters,2008,78.

[3]Ammar M S,Kundu D.Bayes Estimators for Reliability Measures in Geometric Distribution Model Using Masked System Life Test Data[J].Computational Statistics&Data Analysis,2008,52.

[4]周伟萍,张德然,杨兴琼.熵损失函数下几何分布参数的Bayes估计[J].山西师范大学学报(自然科学版)，2007，(4).

[5]周伟萍,张德然,杨兴琼.熵损失函数下几何分布可靠度的Bayes估计[J].数理统计与管理，2008，(1).

[6]熊常伟,张德然,张怡.Q对称熵损失下几何分布的参数估计[J].贵州师范大学学报(自然科学版)，2007，(3).

[7]韩明,崔玉萍.几何分布可靠度估计[J].运筹与管理，2001，(4).

O212.8

A

1002－6487（2011）04－0153-02

吉林省教育厅“十一五”科学技术研究项目(2010);四平市科技发展计划基金项目(2009016)

徐宝(1977-)，男，吉林四平人，博士研究生，讲师，研究方向：数理统计。

（责任编辑/易永生）