基于ARMA-GARCH模型的股市量价动态关系研究

李 丽

(深圳信息职业技术学院 信息经济系，广东 深圳 518029)

基于ARMA-GARCH模型的股市量价动态关系研究

李 丽1,2

(深圳信息职业技术学院 信息经济系，广东 深圳 518029)

文章以GARCH模型为基础，纳入ARMA结构的均值方程形式，建立了描述股价和成交量之间内在关系的ARMA-GARCH组合预测模型。基于股价和成交量的历史高频交易数据，对该模型进行了参数估计和检验，同时对我国股市量价动态关系进行了实证分析。研究结果显示，股价与成交量之间的动态条件相关关系并非常数，而是具有时变性。在整个样本区间，动态条件相关系数均为正，而且随着进出市场的信息流呈现出很强的波动性特征。

ARMA-GARCH模型；股价；成交量；动态相关性

股价与成交量之间的关系，至今已成为微观金融领域研究的热点问题，引起了大量学者的兴趣和关注。为了解释和确定股票量价间的关系，国内外学者从不同的角度、选取不同的市场进行了研究。本文以GARCH模型为基础，采用ARMA结构的均值方程形式，建立了描述股价和成交量之间的内在关系的ARMA-GARCH组合预测模型。基于2001年1月4日至2009年9月16日上证综指日收盘价与成交量的历史高频交易数据，本文对该模型进行了参数估计和检验。该模型从一个新的角度描述了股价和成交量之间的内在关系，在完善投资分析理论，为股票的量价分析提供理论支持等方面将具有一定的理论意义和实用价值。

1 DCC-GARCH基本模型及计量经济学检验

1.1 DCC-GARCH基本模型

考虑到股价与成交量序列存在条件异方差，在估计它们之间的条件相关性时，需要把这一特征考虑进来。Engle(2002)提出的DCC-GARCH模型提供了一种将条件波动和条件相关性结合起来的方法[14]。与GARCH类模型对条件波动建模一样，条件相关的当前值与其滞后值和滞后平方差有关。DCC-GARCH模型的条件方差-协方差矩阵为：

其中，rt是一个 n×n 向量，Ht是条件协方差矩阵，Rt={ρij}t是条件相关性矩阵。Dt=diag{}是从一元GARCH模型得到的n×n对角时变标准差矩阵。Dt的元素服从一元GARCH(p,q)过程：

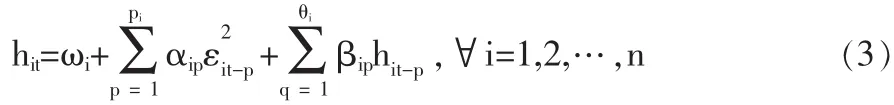
将rt除以它的条件标准差，得到标准化向量rt，εt～N（0，Rt）。

其动态相关结构设定为：

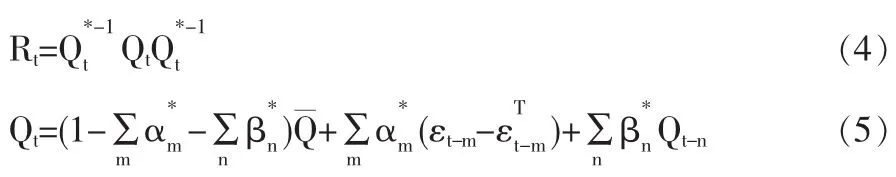
这里Q*t是包含Qt的对角元素平方根的对角矩阵，Qt是由第一阶段估计得到的条件方差-协方差矩阵。Q軍是从Qt计算得到的加权平均矩阵，是标准差的非条件协方差矩阵；εt-m,是标准化残差的滞后值；Q是条件协方差的滞后值。这t-n个模型需要估计额外两个参数：和。DCC-GARCH 模型可以运用(拟)极大似然法估计，对数似然式可以表示为：

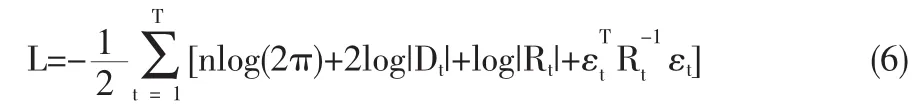
1.2 DCC-GARCH基本模型的计量经济学检验

本文选择2001年1月4日至2009年9月16日上证综指日收盘价与成交量数据，数据来源于清华金融数据库，剔除不匹配数据后，获得样本各2344个。为缓解波动程度，采用对数收益率，即令上证综指、成交量t日的值分别为p1,t和p2,t，则股价收益率SRt和成交量变化率VLt分别为SRt=logp1,tlogp1,t-1，VLt=logp2,t-logp2,t-1，从而得到数据各 2343 个。

对数据建模之前，为防止出现设定错误，有必要大致判断一下数据的统计特征，对数据的描述性检验结果如表1所示。

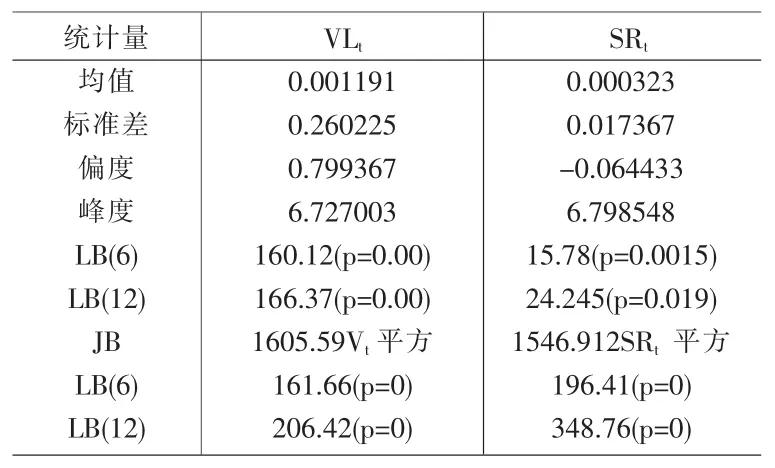
表1 序列的描述性统计

从表1可知，SRt与VLt的Jarque-Bera统计量均拒绝服从正态分布，而且具有“尖峰厚尾”性，因为它们的峰度均大于3。对SRt和VLt滞后6阶和12阶的Ljung-Box检验拒绝了白噪声的零假设，表明存在序列相关，而SRt和VLt平方的Ljung-box检验则表明序列存在ARCH效应。高波动性时期往往之前的波动性也很高，反之也成立，表明存在广泛证实的波动“成群”性。

为防止对非平稳数据回归出现“伪回归”，采用ADF对序列进行平稳性检验，选择显著性水平为1%作为判断标准，结果如表2所示。在1%显著性水平下，检验结果显著拒绝存在单位根的原假设，表明序列是平稳的。因此，采用对数收益率数据进行GARCH建模是可行的。

表2 ADF单位根检验

2 ARM A-GARCH组合预测模型的构建及估算结果

2.1 ARMA-GARCH组合预测模型的构建

估计DCC-GARCH，首先要估计各个收益率的单变量GARCH过程，然后用获得的条件方差hit去除残差得到标准化残差εit，用此标准化残差估计动态相关结构的参数。为了提高模型的拟合优度，下面对GARCH基本模型的形式进行改进。由上述检验可知，序列均存在序列相关，本文在建立单变量GARCH模型的均值方程时，采用ARMA结构。经过多次比较，最后得到均值方程形式为：

括号内分别是t统计量和p值。对上述两个方程残差进行Ljung-Box检验和ARCH-LM检验，结果如表3所示。Ljung-Box检验发现，残差不存在自相关，ARCH-LM检验表明残差序列存在显著的ARCH效应，因此可以进一步建立GARCH模型进行分析。

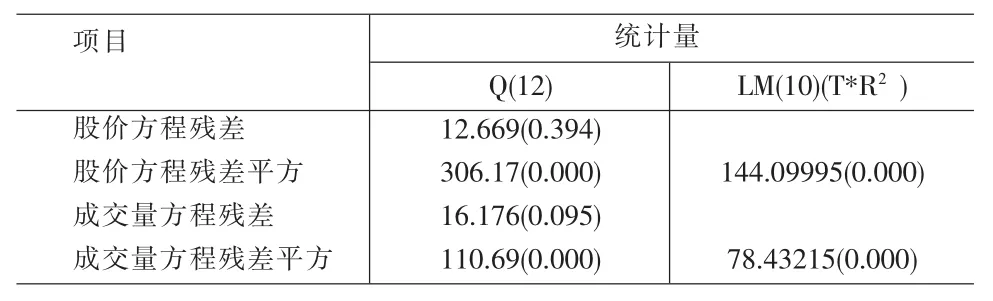
表3 ARMA模型残差检验

按照上面确定的均值方程，用GARCH(1,1)模型对收益率波动性重新拟合，结果如表4所示。

表4 GARCH(1,1)模型估计结果

对各单变量GARCH(1,1)模型的残差及其平方进行自相关和ARCH检验，发现残差序列已经无自相关和ARCH效应，说明模型的均值和方差方程设定合理，检验结果如表5所示。

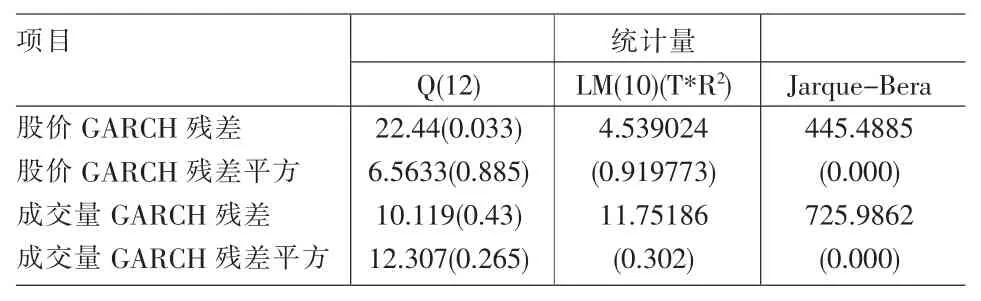
表5 GARCH模型残差检验

GARCH(1,1)估计结果显示，各参数估计量均非常显著，而且α+β接近于1，表明波动具有显著的持续性。

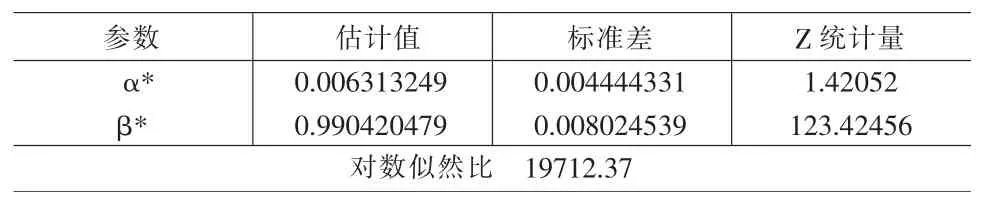
表6 DCC模型估计结果

2.2 ARMA-GARCH组合预测模型的估算结果

Jarque-Bera显示检验残差不服从正态分布，采用拟极大似然估计，得到DCC-GARCH的估计结果，如表6所示。

从估计结果可知，α*很小，表明滞后一期的标准化残差乘积对动态相关系数影响很小，β*非常接近1，表明相关性具有非常强的持续性。动态条件相关系数如图1所示。

动态条件相关系数是金融资产或金融市场趋同程度高低的重要指标。动态条件相关系数高说明资产价格走势趋同程度大，市场一体化程度高，反之，则说明在走势上出现了较大偏差。由于资产市场走势的背后蕴藏着各自的驱动因素，因此，可以透过股价与成交量走势的关系以及由此反映出来的动态条件相关系数对其背后的主导因素进行考察。

从图1可知，在整个样本区间，动态条件相关系数表现出很强的时变性，并且一直为正相关；其次，在时间变化路径上，动态条件相关系数的波动频率和幅度都非常大。从样本初期到2001年10月，动态相关系数在总体上趋于下降，但中间存在小幅波动。从2001年11月开始，动态相关系数开始上升，并一直持续到2002年6月下旬，之后很快下降，但又很快上升，并一直持续震荡性上升到2005年8月的最大点。随后，又持续大幅度下降到2007年6月初的低点。然后，直到样本快结束，动态相关系数呈现出波动程度较大的上升趋势，但在样本最后，似乎又呈现下降趋势。

2.3 实证结果阐释

股市本质上是信息汇总的场所，但不同的投资者对信息的解读不同，造成了异质投资者的产生。预期股价上涨的投资者产生了交易需求，而预期股价下跌的投资者则产生交易供给，交易供给与交易需求的共同作用促使交易行为的产生，也就是说，异质投资者对股价变动信念的不同引起了成交量的产生。对股票而言，市场出清时总存在一个均衡价格，这一价格可能高于股票原来的价格也可能低于原来的价格，这取决于市场对该股票价值的预期是上升还是下降，进而促使成交量的产生并与之对应。一个可能出现例外是当投资者对股价预期朝向同一方向变动时，股价会发生变动，但交易稀少。在具有对称信息时，成交量根据行为人异质性程度而递增；但如果存在信息不对称时，知情交易者与非知情交易者对信息的认知是不同的，不对称程度低时，由信息不对称导致的逆向选择促使交易量增加。若信息不对称程度高，那么具有私人信息的行为人行为就像一个垄断者，非知情人将拒绝交易，因为逆向选择效应超过交易的对冲动机，市场就可能崩盘。

中国是新兴市场，股市的发展在很大程度上依赖国家政策的干预。政策是对股市影响最大的信息，比企业或市场内在因素的改变对市场的影响更大。我国政府经常在股价低迷时进行政策干预，投资者基于这一预期，反应更加激进。另外，我国股市投资者主要是散户，这些投资者承受风险的能力差，容易对股市波动过度反应，急于购入或抛售股票，使市场投机氛围浓厚。而且，散户投资者过滤信息时，注重那些能够增强自信心的信息，而忽视那些伤害自信心的信息，即存在 “损失厌恶”，表现为投资者面对同样数量的收益和损失时，损失带来的效用缺失比收益带来的效用增加大，损失厌恶的投资者引发了交易量的产生。另外，个人投资者在获取、鉴别和利用信息方面的能力较差，收集信息渠道少，对信息缺乏深度解读的能力，而机构投资者拥有资金、信息等优势，可以利用大量的买单和卖单引导股价走势，引起个人投资者在操作上追随机构投资者，追涨杀跌，造成股价与成交量相关性的波动。

从市场微观结构来看，我国股市缺乏做空机制，机构和个人投资者都只能从上涨的股价中获利。政府、机构和个人都对股价上涨具有强烈偏好或意愿。共同愿望会造成市场自动调节机制失灵，股价的调整就只能依赖于外生的强制性措施，使得股价齐涨和齐跌。由于缺乏用于对冲和风险规避的金融衍生工具，使得在牛市中，投资者将资金不断投入股市，促使股价攀升，风险加大。面对加大的风险，投资者只能通过减仓来降低风险，而不能利用衍生品保值。在熊市行情中，投资者只能卖出股票，等待行情见底时建仓，而不能卖空衍生品来减轻股市下跌的压力。因而，股价与成交量之间的动态关系呈现出高波动性。

3 结论

通过对股价与成交量进行GARCH(1,1)估计，然后再对二者之间的动态条件相关关系(DCC)进行估计，得出如下结论：

(1)股价和成交量序列存在显著的ARCH效应，二者的波动具有显著的持久性。股价与成交量之间的动态相关关系并非常数，而是时变的，并且一直是正相关。

(2)DCC-GARCH估计表明，在整个样本区间，股价与成交量之间的动态条件相关系数呈现很强的波动性。

(3)股价与成交量之间的动态条件相关系数不仅取决于二者自身的波动性，还取决于它们对市场信息的响应，尤其是宏观货币政策引起的变化，促使动态相关关系发生结构性变化。

[1]陈怡玲,宋蓬明.中国股市价格变动与交易量关系的实证研究[J].管理科学学报,2000,(2).

[2]王杉,宋蓬明.中国股票市场的简单量价关系模型[J].管理科学学报,2006,(4).

[3]盛建平,高芳敏.成交量与回报率相关性实证研究[J].预测,2000,(5).

[4]Engle R.F.Dynamic Conditional Correlation-a Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models[J].Journal of Business and Economic Statistics,2002,20.

F830.92

A

1002－6487（2011）04－0144-03

李 丽(1982-)，女，湖北荆州人，博士后，讲师，研究方向：经济计量分析与预测等。

（责任编辑/易永生）