消费习惯、递归效用函数与股权溢价
2011-10-24徐成贤
陈 静,徐成贤
(西安交通大学a.经济与金融学院,西安 710061;b.理学院,西安 710049)
消费习惯、递归效用函数与股权溢价
陈 静a,徐成贤b
(西安交通大学a.经济与金融学院,西安 710061;b.理学院,西安 710049)
文章构造了基于习惯形成—递归效用函数的消费—资产组合投资模型,所提出的模型是对 Merton(1973)、Bakshi和 Chen(1996a)、Anne Epaulard 和 Aude Pommeret(2003)研究的推广。 通过对模型求最优解,并利用投资者的行为参数与消费习惯参数进行模拟计算,发现在不同的参数数值下,所得出的投资者相对风险规避系数是合理的。因此,论文提出的消费投资组合模型在一定程度上解释了股票溢价之谜。
递归效用函数;习惯形成;股权溢价
0 引言
传统的资产定价理论无法解释诸多金融市场异像,由此衍生出了诸如股票溢价之谜[1]以及无风险利率之谜[2]。基于传统理论所采用的效用函数所内含的常相对风险规避的偏好结构可能在现实中难以描述实现,很多学者尝试通过修正投资者的偏好结构对资产定价理论进行重构。Duesenberry将消费者的习惯会受过往消费水平的影响称之为“棘轮效应”,对应到资产定价的模型中,我们用消费习惯来表示。Campell和Cochrane[3]认为习惯形成描述了重复刺激会减弱投资者对于刺激的感知能力和反应能力。根据Constantinides[4]在Merton[5]研究,将消费习惯引入消费—资产组合模型,可以部分解释股票溢价之谜。传统的资产定价模型还有一个缺陷:即认为投资者的相对风险厌恶系数应该等于跨期替代弹性系数的倒数,这与两者一个为期内风险规避另一个为跨期风险规避的属性是相悖的。基于此,Epstein和Zin[6]在Kreps和Porteus[7]的理论框架上更加灵活的递归效用函数,利用两个独立参数分别刻画风险厌恶系数与跨期替代弹性系数,推广了传统的时间可分、状态可分效用函数。
已有文献很少将消费习惯与递归效用函数结合起来综合考虑,陈彦斌和徐绪松[8]选用传统的CRRA函数作为效用函数,并引入消费习惯考虑了基于该效用函数的消费投资组合模型。但是文中并没有采用递归效用函数,因此仍然没有区分投资者的两种不同风险偏好行为。基于此,本文拟在Anne Epaulard和 Aude Pommeret[9]的递归效用函数基础上,将投资者的消费习惯引入效用函数中,提出一个综合的效用函数模型。并在此模型基础上,求解基于此效用函数的最优消费与投资组合,在给出习惯—消费比的稳定分布后,计算投资者的平均相对风险规避系数。最好,通过对模拟投资者的行为参数与消费习惯进行分析,验证本文提出的模型对于股票溢价的解释能力。
1 基于消费习惯的递归效用函数
本文的代表性投资者目标函数设定为
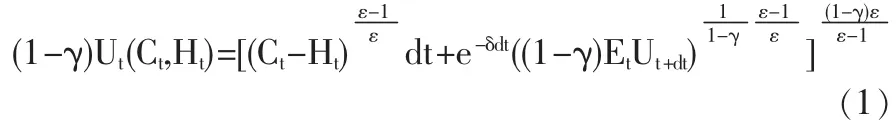
这里,γ≠1是相对风险规避系数,ε>0且ε≠1是跨期替代弹性,δ是主观体现因子。依据Constantinides(1990)[4]对习惯的定义,将Ht定义为习惯存量,即为过去消费率的加权平均和,具体形式如下

其中,参数b度量习惯相对与消费的强度,参数a度量过去消费进入习惯的衰减速度。a越大,决定Ht所给过去消费的权重就越小;b越大,在消费和习惯两者之间所给习惯形成的权重就越小。对式(2)微分得到

γ与ε为两个独立参数,当γ=1/ε时,递归效用函数就退化为时间可分的带消费习惯的幂效用函数,并且其相对风险规避系数就是γ,形式如下
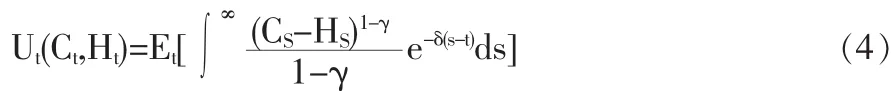
如果再假设,H0=0,即代表性消费者在0时刻的消费习惯为0,并且a=b=0,那么递归效用函数就退化为传统的时间可分的幂效用函数。
可以看出,本文所提出的递归效用函数形式与Anne Epaulard 和 Aude Pommeret(2003)[9]不同之处在于经济中代表性消费者的效用函数,不但依赖于当前的消费Ct,还依赖于习惯存量Ht。
2 消费—资产组合投资问题
本文只考虑一个没有税收并且没有摩擦的经济。假设经济中只存在一种商品,它可以用来消费,也可用作投资,并且只可以投资与以下两种商品:一种无风险资产和一种风险资产。假定无风险资产的收益率为常数r;风险资产的t时价格为pt,服从如下几何布朗运动:

其中,Bt是标准布朗运动;u和σ分别是单位时间内风险资产的收益率的条件均值和条件标准差,均为常数。令w为投资者投资于风险资产的比重。假定投资者没有劳动收入并且没有任何禀赋,因此,投资者为了使生命期内总效用最大,只有通过选择最优的消费分配和资产组合投资:

约束条件为:
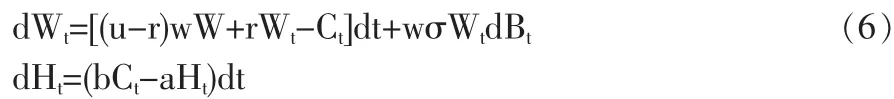
为了简便记号,在不引起混淆的情况下,下面省略记号t。
定理1 若投资者的效用函数为式(1),那么投资者规划问题的最优消费为:

最优资产组合规则为:

而且规划问题的值函数为:

式中参数θ、h和D为:
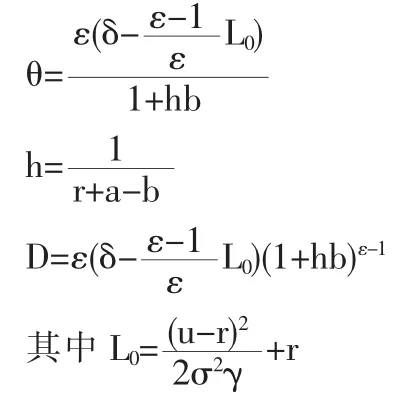
限于本定理证明占用篇幅较长,详细证明可以向读者索取。
从最优消费(7)和投资组合规则(8)可以发现,最优的消费与投资数量均为财富和习惯的线性函数。此性质与Merton(1973)[5]的基于消费的最优解、Bakshi 和 Chen(1996a)[10]的基于财富偏好的最优解以及陈彦斌、徐绪松(2005)[8]的基于财富和习惯的最优解的线性性质是一致的。但是,与前文不同:本文采用了递归效用函数替代传统的CRRA型效用函数,将相对风险规避系数和跨期替代弹性系数分开考虑,不难验证,上述三个模型的最优解均为定理1的特例,例如当γ=1/ε时,即 Constantinides(1990)[4]所采用的基于习惯形成的效用函数:此时,θ、h 和 D 与 Constaintinides(1990)[4]的解完全一样。
3 股票溢价问题
本段采用上一部分所得出的最优解进行分析,首先我们给出基于消费—消费比的稳定分布,然后通过对主观贴现因子和跨期替代弹性系数进行模拟分析,验证本文模型对于股票溢价的解释能力。
3.1 稳定分布
定义投资者的习惯-消费比率为

定义另外一个比率为

显然有

由于比率yt和zt是消费、习惯的函数,因此一般说来,这两个比率的分布函数随时间变化而变化。下面我们证明,只要满足一定的条件,比率yt和zt具有稳定分布函数的条件,并给出两者相应的稳定分布函数。
定理2 如果b+2(C0)2-A0-a-B0+2C0D0<0,那么
(1)扩散过程yt存在稳定分布,并且其概率密度函数有如下形式
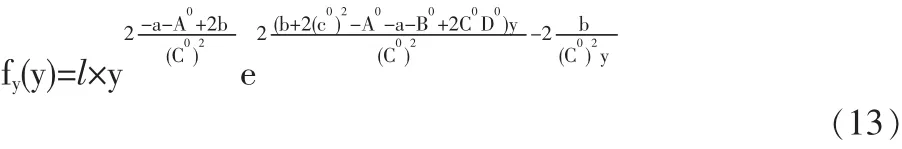
此处l是常数,以使fy(y)规范化。
(2)扩散过程zt存在稳定分布,并且其概率密度函数有如下形式

此处 0 证明 (1)对z=H/C使用Ito定理,有 此处,P(z)=A0+B0z,Q(z)=C0+D0z。 对y=z/(1-z)使用Ito定理,得到 根据Fokker-Planck公式,有 根据Merton(1975)[11]的相关研究,可知0和∞是y的不可达的边界点,所以y是一个没有吸收态的常返马氏过程,即y存在一个非平凡的严平稳分布。所以鄣fy=0。 因此,式鄣t(13)即为式(17)的解。 (2)根据 y和 z的定义,有 fz(z)=fy(y) 将式(13)代入上式,就得到所以的结果,即方程(14)。 用比率zt的概率密度函数来计算最优消费增长率的无条件均值和方差。下面的定理2给出最优消费增长率所服从的随机过程,无条件均值及其方差。 定理3 (1)最优消费的增长率服从如下扩散过程 其中,P(zt)=A0+B0zt,Q(zt)=C0+D0z,A0,B0,C0和 D0的定义同定理2。 (2)最优消费的无条件均值为 最优消费增长率的无条件方差为 证明:(1)对最优消费规则 C=H+θ(W-hH)=θW+(1-θh)H微分,可以得到消费所服从的随机微分方程 dC=θdW+(1-θh)dH 上式两边同除以消费,并根据式(22)得到 dC/C=θdW/C+(1-θh)(b-az)dt 结合财富的动态方程和最优资产组合,得到 利用 C=θW+(1-θh)H,可以得到 将W/C代入dW/C,有 再将dW/C代入dC/C,可以得到 (2)将P(zt)和 Q(zt)的表达式代入消费增长率,取期望与方差就得到所需的结果。 与 Constantinides(1990)[4]一致,定义投资者的相对风险规避系数(Relative Risk Aversion,简称RRA)为 将式(9)代入(21),得到 根据式(22)可以看出,RRA系数是随机的,并且可以表示为yt的函数,由于yt存在稳定的分布函数,因此,投资者的RRA系数也具有稳定分布,英寸,可以用其来计算代表性投资者的相对风险规避系数均值。 本部分拟利用本文提出的模型并使用数值模拟技术研究股权溢价问题。采用与Merha和 Prescott[1]的研究一致的数据,所选取模型的参数值为u=0.07,r=0.01。δ=0.037,因此,本文模型的参数,除了四元组(a,b,γ,ε),已经全部设定了。 考虑不同的四元组(a,b,γ,ε),计算平均 RRA 系数的值。表1和表2分别给出了当γ,ε取值给定时,不同的消费习惯参数 a,b所对应的 E(RRA)以及当 a,b取值给定时,不同的相对风险规避系数γ和跨期替代弹性系数ε所对应的E(RRA)数值。可以看出,两个表中的平均RRA系数都在3左右,因此,可以认为,本文所提出的消费—资产组合选择模型可以在一定程度上解释股票溢价之谜。 表1 γ=2.2,ε=2情形下不同a,b值对应的E(RRA)数值 表2 a=0.1,b=0.93情形下不同γ,ε值对应的E(RRA)数值 与Constantinides(1990)仅引入消费习惯不同,本文构造了一个新的消费投资组合模型,通过将习惯形成引入到投资者的效用函数中,可以将投资者的跨期替代与风险规避两种不同时际的风险偏好区别开。接着对模型计算最优解,并利用不同的参数模拟投资者的主观贴现因子和跨期替代弹性系数,发现在不同的参数数值下,投资者的相对风险规避系数的均值基本都小于3,这与传统的风险规避系数应该在2左右是相符的。因此,本文提出的消费投资组合模型在一定程度上解释了股票溢价之谜。 已有的一些文献很少结合财富偏好于递归效用函数进行分析,根据巴克希和陈(Bakshi and Chen,1996a)的研究,财富偏好可以一定程度上解释无风险利率之谜。基于此,本文后续研究,将结合本文的理论模型,适当引入财富偏好,进一步讨论结合消费习惯与财富偏好视角的消费投资组合模型。 [1]Mehra,R.,Prescott,E.C.The Equity Premium:A Puzzle[J].Journal of Monetary Economics,1985,(15). [2]Weil,Philippe.The Equity Premium Puzzle and the Risk-free Rate Puzzle[J].Journal of Monetary Economics,1989,(24). [3]Campbell,John Y.,John H.Cochrane.By Force of Habit:A Consumption-Based Explanation of Aggregate Stock Market Behavior[J].Journal of Political Economy,1999,(107). [4]Constantinides,G.M.Habit Formation,a Resolution of the Equity Premium[J].Journal of Political Economy,1990,(98). [5]Merton R.C.An Intertemporal Capital Asset Pricing Model[J].E-conometria,1973,(41). [6]Epstein,Larry G.,Stanley E.Zin.Substitution,Risk Aversion,and the Temporal Behavior of Consumption and Asset Returns,an Emprical Analysis[J].Journal of Political Economy,1991,(99). [7]Kreps,D.M.,E.L.Porteus.Temporal Resolution of Uncertainty and Dynamic Choice Theory[J].Econonometrica,1978,(46). [8]陈彦斌,徐绪松.财富偏好、习惯形成与股票溢价之谜[J].统计与决策,2005,(12). [9]Anne Epaulard,Aude Pommeret.Recursive Utility,Growth,and the Welfare Cost of Volatility[J].Review of Economic Dynamics,2003,6(2). [10]Bakshi,Gurdip S.,Zhiwu Chen.The Spirit of Capitalism and Stock-Market Prices[J].American Economic,1996a,(86). [11]Merton R.C.An Asymptotic Theory of Growth under Uncertainty[J].Review of Economics and Statistics,1975,(42). O212 A 1002-6487(2011)04-0141-03 国家自然科学基金资助项目(10971162) 陈 静(1963-),女,河北唐山人,博士研究生,研究方向:金融工程、证券投资分析。 (责任编辑/浩 天)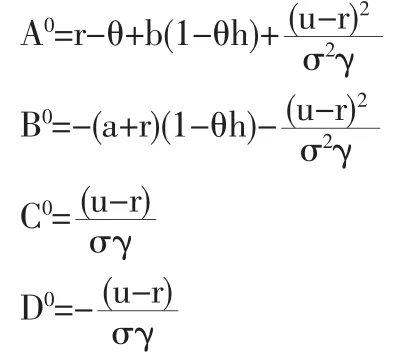
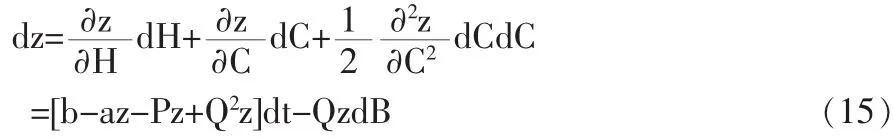
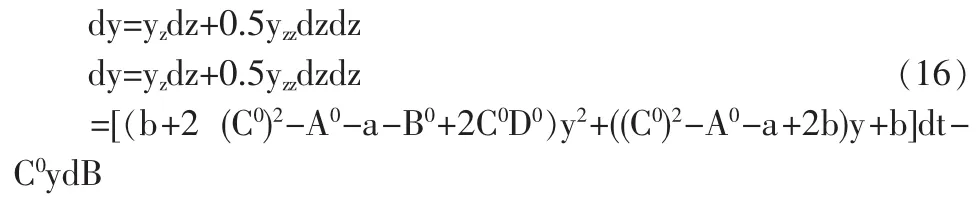
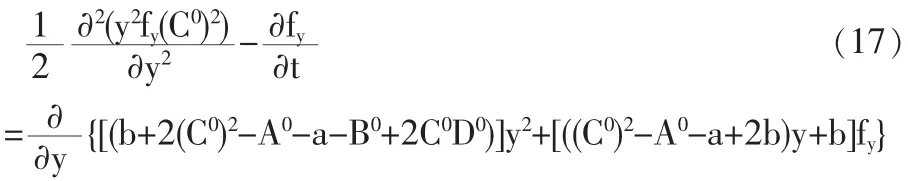


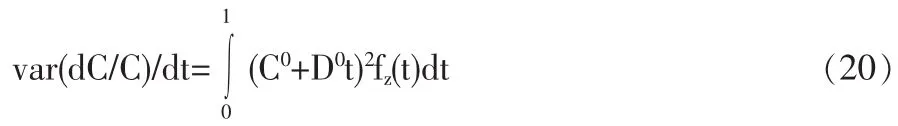
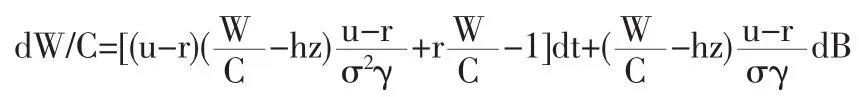


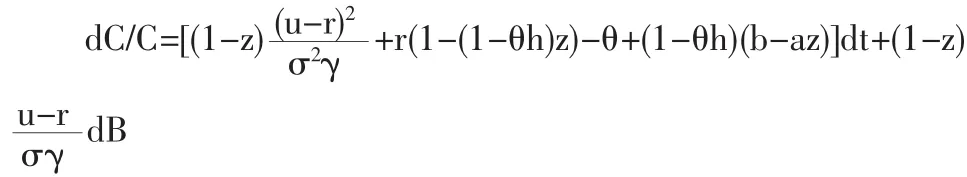
3.2 相对风险规避系数


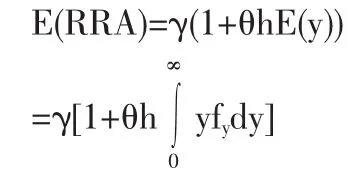
3.3 数值模拟


4 结论
