基于DEA的模糊点数据回归分析

彭 煜，张兴娟，贺 唐，陈思颖，盛文文

（西南科技大学 经济管理学院，四川 绵阳 621010）

基于DEA的模糊点数据回归分析

彭 煜，张兴娟，贺 唐，陈思颖，盛文文

（西南科技大学 经济管理学院，四川 绵阳 621010）

对每个训练数据的DEA有效值作为它的模糊隶属度，以表示训练数据对总体的贡献程度。从DEA的视角，获取模糊点数据，得到了基于模糊点数据的最小二乘估计，及其一些优良的统计性质。利用平均相对贴近度，给出了一个评价模型拟合效果的准则。通过数值实例的计算比较，表明了该方法的有效性。

数据包络分析（DEA）；模糊点数据；平均相对贴近度；回归分析

1 模糊点数据

在经典回归分析中，认为所有数据点对拟合曲线的贡献是相同的，但在很多实际问题中，每个数据对总体来说具有不同的意义，有些数据相比于其他数据来说显得更重要。

假设x是k维预报变量，Y是一维响应变量，(xj,yj)是训练样本。在这里我们给每个训练数据赋予一个模糊隶属度 θj（0≤θj≤1），将其认为是对应的数据点对总体的重要程度。称((xj,yj),θj)为 Rk+1中的模糊点，定义{(xj,yj),θj：j=1,2,…,n}为模糊点集。

设n个决策单元DMUj，j=1,2,…,n。每个DMUj都有k种输入 Xj=(x1j,x2j,…,xkj)，s 种输出 Yj=(y1j,y2j,…,ysj)，评价 DMUj0(xj0,yj0)相对有效性的BCC模型为：

其中θ为决策单元DMUj0的相对有效性值，把θ作为隶属度，赋予决策单元所对应的训练数据。

2 基于模糊点数据的最小二乘回归

2.1 最小二乘回归

假设有一个k维输入向量X=(x1,x2,…,xk)，用下面的模型预测输出Y：

其中β0,β1,…,βk是待估计的未知参数。对于训练数据集{(xi,yi);i=1,2,…,n}，其中 xi=(xi1,xi2,…,xik)t，它们满足：

其中 X,Y,β,ε 分别是：

误差项 εi，i=1,2,…,n，满足 Gauss-Markov 假设。

记e=Y-Xβ，选择系数β以最小化残差平方和：

2.2 基于模糊点数据的最小二乘回归

假设给定一个有模糊权重的训练点数据集：

((x1,y1),θ1),((x2,y2),θ2),…,((xn,yn),θn)

给定每个训练点xi∈Rk+1和模糊隶属度θi(0≤θi≤1),i=1,2,…,n，构建基于模糊点数据的线性回归模型：

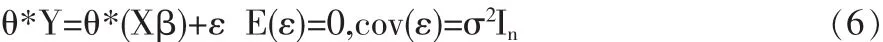
其中运算“*”的定义如下：记

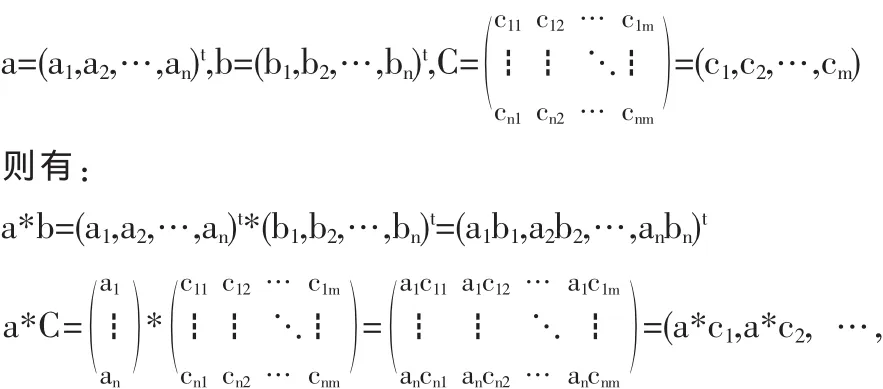
2.3 基于模糊点数据的最小二乘估计的性质

类似于文献[2]的方法，可以得到基于模糊点数据的最小二乘估计具有许多优良性质。

定理 2 对于基于模糊点数据的线性回归模型 （6），在CTβ的所有线性无偏估计中，最小二乘估计赞是唯一具有最小方差的估计。

误差向量E=θ*(Y-Xβ)，用基于模糊点数据的最小二乘估计赞代替其中的β，得到残差向量：

因此，对于基于模糊点数据的线性回归模型（6），用常规的方法可以证明下面的定理。

定理 4 假设误差向量 ε～N(0,σ2I)，则有：

对于模糊点数据的回归分析，我们定义样本相对平均贴近度。

定义：基于模糊点数据集：

按（6）进行线性回归。样本的平均相对贴近度为：

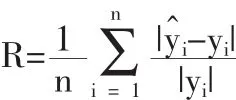
它反映了模型拟合值与样本观测值之间的平均相对接近程度。

3 数值实例

以国内生产总值GDP表示产出，资本形成总额表示资本投入，就业人数表示劳动投入，基于1990~2007年河南省的统计数据（来自2008年河南省统计年鉴），对生产函数进行回归分析，分别用两种不同的方法确定隶属度。

方法一。线性函数方法。文献[2]给出了确定模糊隶属度的线性函数和二次函数方法，下面按线性函数方法确定隶属度。对于给定的数据点序列：

其中t1≤t2≤…≤tn是数据点到达系统的时间。设si是ti的函数，认为最后一个点xn是最重要的并且选择sn=f(tn)=1，认为第一个点x1最不重要并且选择s1=f(t1)=σ。使得模糊隶属函数是时间的线性函数：

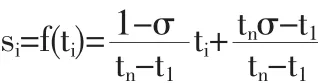
本文中令σ=0.9，计算出对应于1990~2007年度的18个隶属度取值如表1所示：

表1 线性函数法计算的各个训练数据的隶属度值

方法二。基于DEA方法确定的隶属度。将收集到的统计数据代人（1），并使用Matlab进行上机运算，得到的结果如表2。

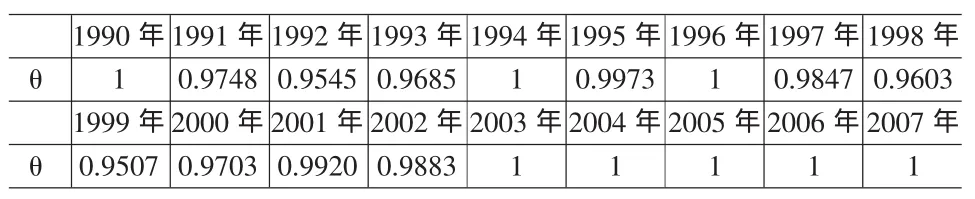
表2 DEA方法计算的各个训练数据的隶属度值

分别将上述两种方法得到的s、θ结果作为模糊隶属度，对河南省1990~2007年的数据进行回归分析，记两种方法得到的 GDP 拟合值分别为回归计算的结果为：

按传统的方法，对原始数据进行回归分析，得到的GDP拟合值为

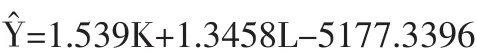
记真实的GDP值为Y，对三种回归分析的结果进行分析，分别计算如表3。

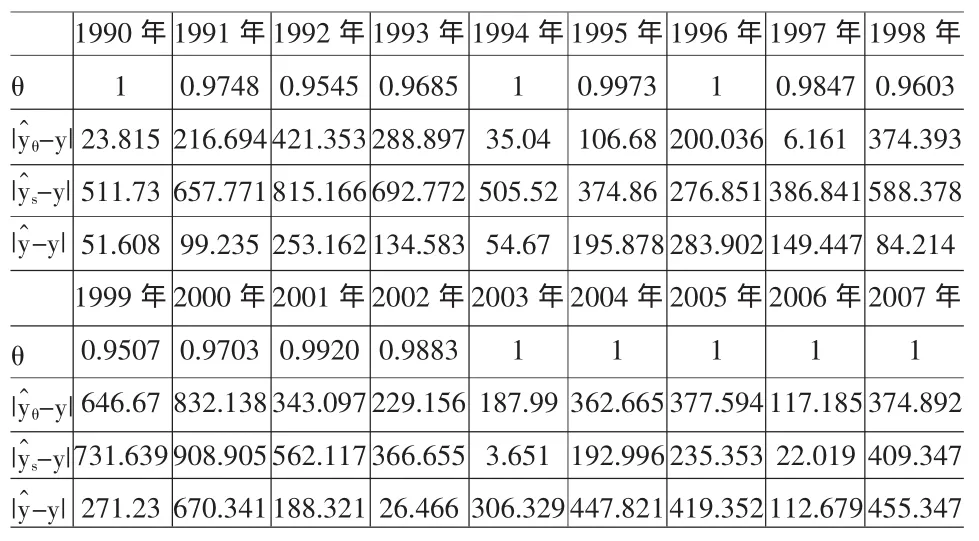
表3 三种回归分析的残差绝对值

从上面的计算可以发现，相应于1990年、1994年、1995年、1996年、1997年、2003 年、2004 年、2005年、2006 年及2007 年的数据对比来看，|都要小于，而这些年份恰好对应着较大的模糊权重。从而可以说明在模糊线性回归中，权重越大的模糊点数据对拟合曲线的贡献也就越大，这与文献[2]得出的结论是一致的。残差绝对值总量、平均相对贴近度的计算结果为：

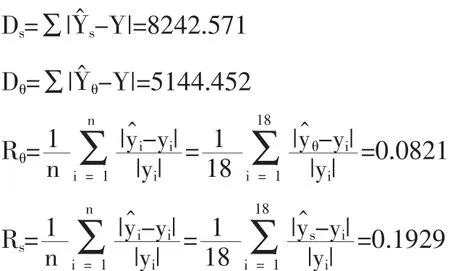
可以发现 Dθ

4 结论

用DEA的方法为数据确定模糊隶属度，从DEA的角度将模糊性引入回归分析中，是一种确定隶属度的客观方法。从理论分析和数值实例两个方面，表明该方法不仅具有优良统计性质，还从不同的角度进一步证明了模糊权重越大的数据对拟合曲线的贡献越大，与其它确定隶属度的方法相对比，基于DEA的隶属度确定法要优于传统的确定隶属度的方法。

[1]李正，宋保维，潘光，皮德福.无失效数据参数估计的模糊回归法[J].机械设计，2005,22（3）.

[2]沈菊红.基于模糊点数据的线性回归分析[J].黑龙江大学自然科学学报,2007，(6).

[3]沈菊红.基于模糊点数据的Logistic回归模型[J].宁夏师范学院学报（自然科学），2007，（3）.

[4]沈菊红.基于模糊点数据的线性回归模型在判别分析中的应用[J].宁夏大学学报（自然科学版），2008，（4）.

[5]王惠惠，魏立力.基于模糊点数据的回归变点识别[J].计算机应用,2007，(06).

[6]李竹渝,张成.模糊数据的回归模型结构分析[J].统计研究,2008,25(8).

[7]龙海亮.基于DEA回归的C-D生产函数分析[J].内蒙古农业科技,2008，(2).

[8]全林，罗洪浪．基于Bootstrap方法数据包络分析的回归分析[J]．上海交通大学学报，2005，39（10）.

[9]James Odeck.Statistical Precision of DEA and Malmquist Indices:A Bootstrap Application to Norwegian Grain Producers[J].Omega,2009,37.

（责任编辑/易永生）

C812

A

1002－6487（2011）03－0170-03

彭 煜（1963-），男，湖南永州人，博士，教授，研究方向：应用数学，决策分析。

张兴娟（1986-），女，甘肃古浪人，硕士研究生，研究方向：循环经济。