金融市场风险的极值模型及实证分析

2011-10-24黎德元叶金娥

统计与决策 2011年3期

关键词：门限极值度量

黎德元，叶金娥

（复旦大学管理学院，上海 200433）

金融市场风险的极值模型及实证分析

黎德元，叶金娥

（复旦大学管理学院，上海 200433）

风险值（VaR）是金融市场风险的度量指标，选择好的计算方法十分重要。文章主要应用极值理论中的门限模型来研究风险值，并对2000年以来深圳综指和上证指数的日对数收益率计算风险值和期望亏损，最后对两市的风险进行了比较。

极值理论；门限模型；风险值；期望亏损；广义帕累托分布

0 引言

随着全球金融市场的发展和金融创新的深化，金融市场的波动性和脆弱性也不断加剧。1987年华尔街的股市大崩盘，20世纪90年代长期资本管理公司的倒台，20世纪末的东亚金融危机以及2008年由美国次贷危机引发的全球金融海啸等，这一系列极端风险事件的出现，促使金融从业者和研究者寻求新的方法和工具，从而加深对金融风险管理的认识。按照国际清算银行的要求，银行和其他金融机构已经开始在遵循管制的基础上度量其面临的市场风险，并产生了一个全球一致的度量市场风险的概念——风险值（VaR）。J.P.Morgan在风险度量中将VaR定义为 “VaR是按照预定的置信度，对所持有头寸在某一间隔期上可能遭受损失的一个估计，对典型的交易活动，间隔期也许是一天，对资产组合管理也许是一个月或更长……”。简言之，VaR就是在一定的持有期及一定的置信度内，某金融工具或投资组合所面临的潜在的最大损失。

用统计语言来说，如果用△V(詛)表示金融资产头寸从第t期到第t+詛期的价值变动，置信度为1-p、时间跨度为詛的VaR满足：

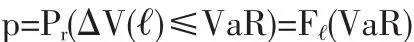
其中F詛是时间跨度为詛的金融资产头寸价值的分布函数。如果数据是收益率,那么这里的分布函数就表示收益率的分布。也就是说，多头资产持有者在时间跨度内詛的收益小于等于VaR(VaR为负时，表示损失)的概率为p。当资产价值增加 △V(詛)（△V(詛)>0）时，空头头寸持有者遭受损失，此时VaR定义为：

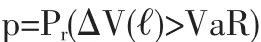
传统的VaR计算方法都考虑收益率的整体分布，例如假设收益率服从正态分布。极值理论研究分布的尾部。由于分布的尾部反映的是潜在的灾难性事件导致的金融机构的重大损失，所以风险管理者更注重分布的尾部。许多研究表明大多数金融数据是重尾的，因此传统的分布假设并没有很好地刻画尾部特征（参见文献[1]）。只对尾部进行假设，这是极值理论应用于VaR计算上的最大优势。

1 极值理论的门限模型

1.1 广义极值分布（GEV）

定理 1 假设随机变量 X，X1，X2，…，Xn，独立同分布于分布函数 F，Mn为样本最大值，即 Mn=max(X1，X2，…，Xn)。假设存在常数序列{an>0}和{bn∈R}使得对某个非退化的分布函数G有

其定义域为{z:1+ξ(z-μ)/σ>0}，μ，ξ∈R，σ>0。

称满足（1）的分布函数F属于G的极大吸引域，并记作F∈MAD(G)。其中，ξ为形状参数，σ为尺度参数。当ξ=0时，G相应地取其极限，即

1.2 广义帕累托分布（GPD）

定理2 假设X 茗F且F∈MAD(G)，则对于充分大的u，

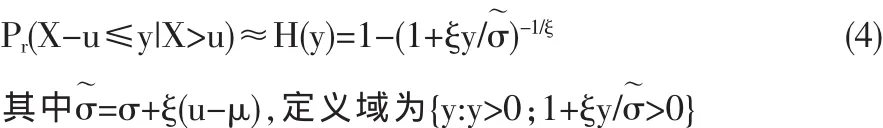
这里的分布函数H就称为广义帕累托分布，形状参数ξ与极值分布的相应参数相同。ξ=0时，H即为指数分布。定理1与2的证明可见参考文献[2]。

1.3 门限模型

所谓门限模型，就是取一个相对较大的阈值u（称为门限），并假设随机变量超出门限的部分近似为GPD。在门限模型中，需要选择一个合适的门限，然后估计参数，并用拟合的模型计算分位数、做模型诊断等。

2 模型的建立

2.1 门限选择

在给定门限u的情况下，提取出那些超过门限的观测值，并重新记为 x(1)，x(2)，…，x(k)，其中 k 为超过门限的观测值个数。定义超出量 yi=x(i)-u，i=1，2，…，k。根据定理 2，可以近似认为{yi，i=1，2，…，k}是来自 GPD 的一个样本。

门限选择要考虑到估计量的方差和偏差的平衡：如果门限过大，则实际使用数据量过少，造成估计量的方差较大；如果门限过小，则超出量的分布与GPD偏离会比较大。通常的原则是在保证极限分布能较合理地被GDP近似下，尽量选择较低的门限。有两种方法可用：其一是在参数估计前进行的探索性分析；另一方法是选择一系列门限，然后分别拟合模型，并根据参数估计的稳定性确定合适的门限。

具体地说，第一种方法以GPD的期望为基础。假设对于随机变量X，其关于某门限u0的超出量分布为GPD。当ξ≥1时，超出量的期望不存在。当ξ<1时，超出量的期望为：E（X-如果GPD对门限u成立，则对所有大于u

00的门限u也应当成立，只是尺度参数相应地变为σu。因此，

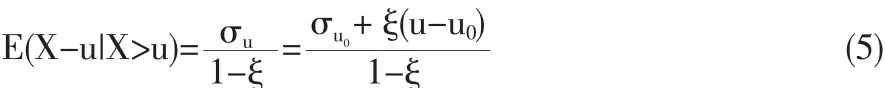
故可选取一系列门限值，用超出量的样本均值代替条件期望，得到一个轨迹图：

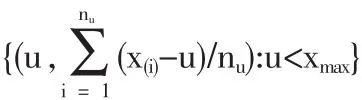
其中 x(1)，x(2)，…，x(nu)表示所有超过 u 的样本，xmax为所有样本的最大值。该轨迹图称为残余生命图(Residual Life Plot)。选择门限u0，使得对u>u0时轨迹为线性的。

另一个方法是从参数的稳定性考虑的。由定理2知道σu=σu0+ξ(u-u0)，则 σ*=σu-ξu 关于 u 不变。而形状参数 ξ关于u也是不变的。选取一系列u，分别估计出参数，画出轨迹图。选取门限u0使得ξ和σ*关于u>u0稳定。

2.2 参数估计

已经得到了门限u，GPD的参数可以由极大似然方法估计。对于ξ≠0，对数极大似然函数为：

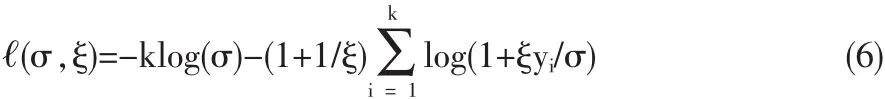
其中 ξ，σ 满足：1+ξyi/σ>0，i=1，2，…，k。对于 ξ=0，相应地有：

通常可由数值计算方法（如Newton-Raphson方法）求得参数的极大似然估计，并通过信息矩阵得到置信区间。

2.3 风险值与期望损失（ES）计算

假设X是一个表示损失的随机变量，通过上述方法可以求得给定门限u时X的条件概率，接着便可以计算出X在大于门限情形下的无条件概率。对x>u，

其中ζu=Pr(X>u)，可由k/n估计，其中k、n分别为超出量个数和样本量。令上式等于p就可求得1-p分位数，即风险值VaR1-p：

特别地，当 p=1/m，m为整数时，相应的分位数也称为“m次观测的回报水平”，即平均每m次才出现一次超过它的事件。

期望亏损（简称ES）是衡量风险的另一指标，定义为超出风险值VaR的损失大小的期望。当q>F(u)时，

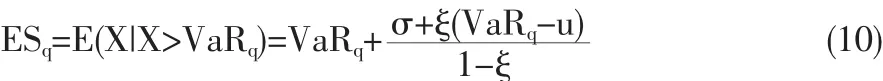
将σ，ξ的极大似然估计代入，便可得到风险值VaR的估计，继而得到期望损失ES。置信区间可通过delta法则或类似然方法求得，方法可参考文献[2]。

2.4 模型诊断

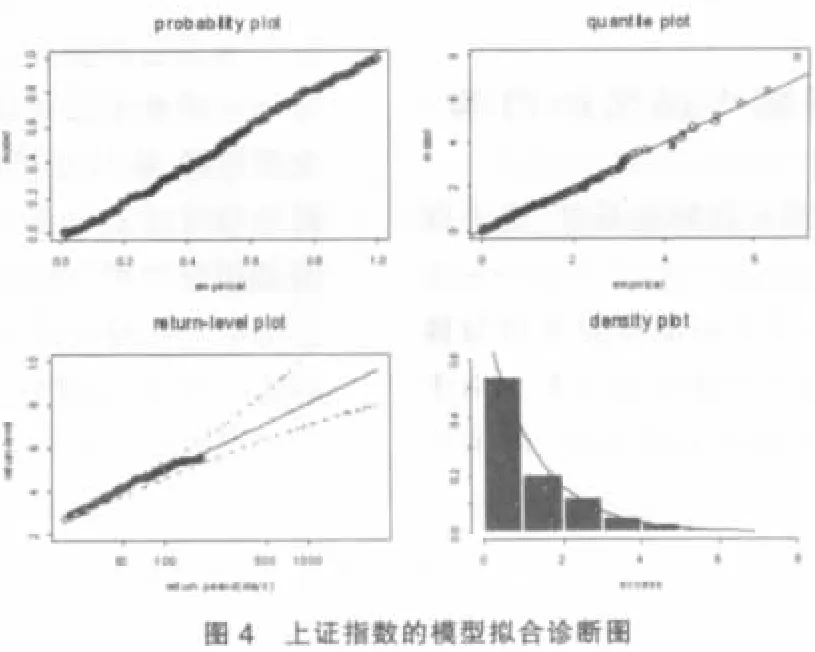
评估一个GPD拟合得是否好，常用方法是概率图、分位数图、return-level图、密度图。提取样本超出量并排序:y(i)，i=1，2，…，k

(1)概率图：比较经验分布函数和拟合的GPD:

其中H为拟合的GPD。

(2)分位数图:比较样本分位点和拟合的GPD的分位点

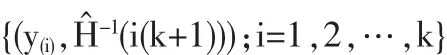
(3)return-level图：{（m，xm）}

xm为m次观测回报水平。常将坐标做“对数化处理”以加强观测效果。同时加入置信上下限和回报水平的经验估计。

(4)密度图：制作超出量的直方图，添加拟合的GPD的密度曲线，并比较。

3 对上证指数、深圳综指的实证分析

上证指数和深证综指分别是由上海、深圳证券交易所根据在各自交易所上市的股票，选择一定的成分股，用成份股的可流通数作为权数，采用综合法进行编制而成的股价指标。它们是中国反映股市总体走势的统计指标，具有良好的市场代表性。本文选取的数据为上证综指、深证综指于2000年1月—2010年6月间的各2524个日收盘价(数据来源：大智慧软件)。定义“日对数收益率”为：Xt=ln(Pt/Pt-1)*100，其中Pt为当日收盘价。所有计算通过S-plus统计软件实现，可以参考文献[4]中关于软件中Finmetrics模块的使用介绍。

3.1 基本描述和统计

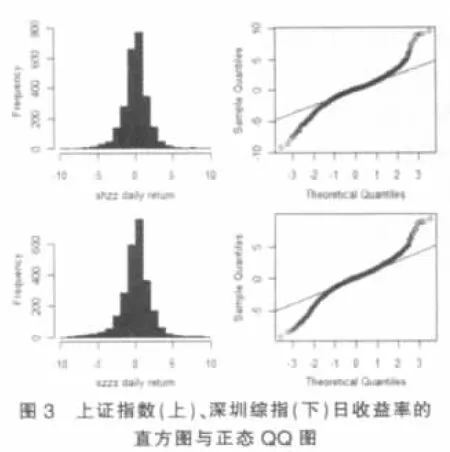
表1给出了深圳综指、上证综指收益率的基本描述性统计。图1、图2分别为两市指数、日对数收益率的走势，可以看到指数数据是非平稳的，而收益率数据近似平稳。图3为两市收益率的直方图、QQ图，可以看出与正态分布相比，它们的分布均尖峰厚尾。通过这些图表，可见两市的特征非常相似，分布左偏，尖峰厚尾。

3.2 模型拟合

由于对多头头寸持有者而言，他们常关心的是收益率的左尾，我们在运用本文所述方法时，用收益率数据的相反数建模，门限选择结合2.1节的2种方法综合确定，其余参数估计用极大似然法，而风险值（VaR)）及期望损失（ES）用类似然方法(Profile Likelihood)得到。

表2给出了模型拟合的参数选择和估计。图4给出了沪市的模型拟合诊断，可见GPD对尾部数据拟合得相当好。深市的模型拟合也是相当好，其拟合诊断图此处略去。

表 1 两市指数日对数收益率的基本统计量比较

表2 参数选择和估计比较

表3 不同置信度下的VaR估计及95%置信区间

表4 不同置信度下的ES估计及95%置信区间

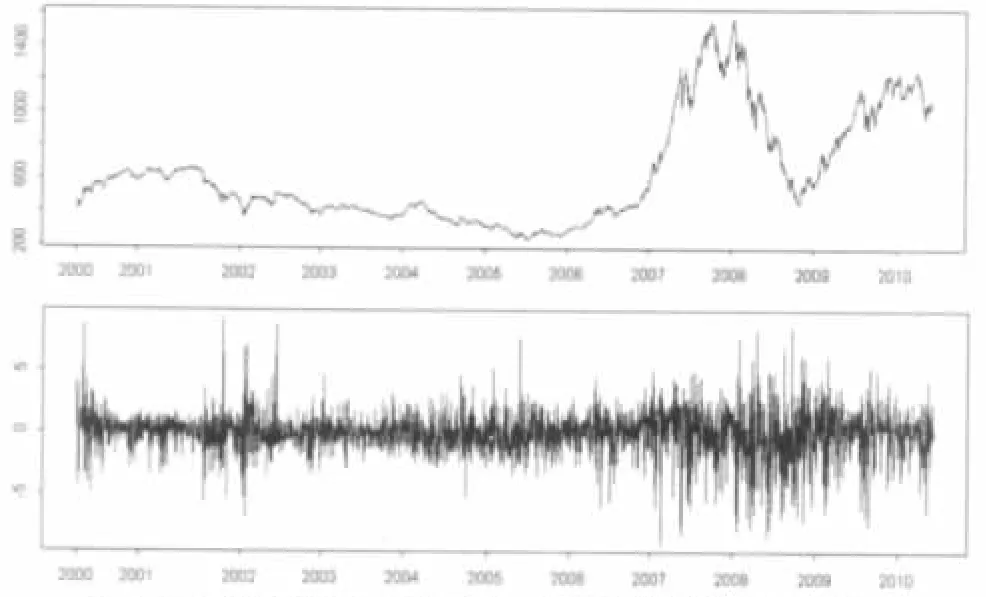
图1 深圳综指日收盘价走势图（上）、日对数收益率走势图（下）

3.3 风险分析

从表3、表4可以看出：相同水平下，深市的VaR及ES都要大于沪市，表明深市股票具有更大的波动性，即具有更大的市场风险。不过，两市指数统计特征相似，风险值接近，说明它们内部有着共动性，这实际上是由于两市都处于中国，受整个中国经济、政策等影响。

4 结论

本文主要介绍了极值理论中的门限模型，并应用于金融市场风险的度量。对2000年以来深圳综指、上证指数进行实证研究，计算风险值（VaR）和期望损失（ES），发现模型拟合得相当好。风险分析表明，深市股票具有更大的市场风险；但两市指数统计特征相似，风险值接近，说明它们内部有着共动性，这实际上是由于两市都处于中国，受整个中国经济、政策等影响。

在具有厚尾分布的金融市场，极值方法不需要对收益的整体分布做出假设，而是让数据来拟合分布的尾部，因此建模的风险减少了。这是极值方法最大的优点。正是由于极值理论在极端条件下估计风险的极大优越性，其在近期得到了广泛的运用，并且在金融风险度量与管理中的良好前景已得到越来越广泛的关注。文献[5]、[6]分别给出了商业银行操作风险、汇率市场风险的极值度量方法。

本文的不恰当之处是：文中门限模型的假设条件是随机变量序列独立同分布，而金融市场的数据往往不满足该条件。不过在一定条件下极值理论对平稳序列也是成立的，在模型运用过程中略作修改即可，可以参考文献[7]，关于VaR和ES的估计结果与假设独立的情况下比较接近。本文使用的收益率数据近似平稳，直接使用独立同分布条件下的门限模型已经拟合得相当好且使用简洁方便。