自适应两阶段设计的性质及样本容量的再估计
2011-10-24言方荣
言方荣
(中国药科大学 数学系,南京 210009)
自适应两阶段设计的性质及样本容量的再估计
言方荣
(中国药科大学 数学系,南京 210009)
临床试验的主要目的是在给定的一些可能有效的治疗中找到一个最佳治疗,并证明所找到的最佳治疗相对于试验控制组的优效性。文章探讨了自适应两阶段试验设计及其在临床Ⅱ/Ⅲ期中的应用,并证明了一些性质。通过计算机模拟给出了有效性检验的临界值与样本容量的关系,指出自适应两阶段试验所需的样本容量比传统的试验设计方法更少,有较高的伦理学价值和经济学价值。
临床Ⅱ/Ⅲ;自适应两阶段试验设计;优效性检验
0 引言
临床试验的主要目的是在给定的一些可能有效的治疗中找到一个最佳治疗,并证明所找到的最佳治疗相对于试验控制组的优效性。传统的临床试验是在临床Ⅱ期确定一个最佳治疗,在临床Ⅲ期证明治疗的优效性,将临床Ⅱ/Ⅲ期看成两个独立的过程。这一方法在实际应用中较为简单,但确存在较大的风险。一旦在第一阶段(临床Ⅱ期)选择了一个错误的最佳治疗,将影响整个试验过程,甚至导致试验的失败。Bischoh和Miller[1]提出了一个自适应两阶段试验设计方法,即将临床Ⅱ/Ⅲ期整合考虑,其基本思想是将第一期试验数据尽可能用到临床Ⅲ期的优效性检验中去,以期尽可能减少整个试验中的受试人数,并选择一个较为可靠的最佳治疗。这一方法有较好的伦理学和经济应用价值。近来相关文献都进行了研究(Bretz,F.[2])等本文将考虑在一般情形下自适应两阶段的相关性质及样本容量的再估计问题,并通过模拟证明自适应两阶段试验优于传统的试验设计过程。
1 自适应两阶段试验设计
假设第i个病人在第k段试验中接受第j个治疗,则

其中,i∈{1,2,…,n};j∈{0,…,t};k∈{1,2};Yijk是第 i个病人在第k段试验中接受第j个治疗观察值,j=0表示控制组,j∈{1,…,t}表示t个治疗组;μj为第j个治疗的平均效应。设 θ 表示最佳治疗方案,则θ赞=argmaxj=1,…,t{μj}。由自适应两阶段设计方法,在试验的第一阶段(临床Ⅱ期)观察Yij1,在试验的第二阶段(临床Ⅲ期)只观察 Yij2.(j∈{0,})。 经典的优效性检验可用如下多重假设检验表示Bechhofer,R.E.[3]:

而对自适应两阶段设计,利用第一阶段中期分析的结果,只需检验

设第j个治疗组有n1个样本,则在试验第一阶段


其中v是属性参数,[·]表示高斯取整函数。由(3)治疗组与控制组优效性的检验只需比较j=0和j=θ赞。记

下讨论基于(4)检验统计量的一些性质。
2 基本性质
定理 1 设 n1∈N,n2,min∈N0,V>0,α>0,μj,{j=0,1, …,t}是t+1个处理效应,则检验临界值u是如下方程的解


表1 样本容量n1与u、v的关系
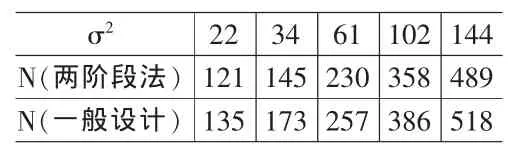
表2 试验样本容量的再估计
3 模拟研究
利用定理1及定理2,通过计算机模拟样本容量n1与临界值u与属性参数v的关系,未知方差σ2与试验所需总体样本容量的关系,并与一般的试验设计相比较。为方面起见,这里仅模拟j=0,1,2情形,即试验中有一个控制组,两个对照组。根据FDA相关规定取检验的水平α=0.025,检验功效1-β=80%,σ2={22,34,61,102,144},μ1-μ2≥△=4。模拟结果如表 1、表 2。
4 讨论
本文讨论了临床Ⅱ/Ⅲ试验设计的两阶段自适应设计法,将临床Ⅱ/Ⅲ过程看成是一个整体的过程。充分利用在试验第一阶段所获得的信息,将它作为第二阶段试验的依据,并用以估计试验中的未知方差。定理1和定理2分别讨论了自适应两阶段设计的一些性质和样本容量的再估计问题,给出了严格的证明。通过模拟,给出了临床Ⅱ期试验所需的样本容量和检验临界值的关系(见表1),并讨论了未知方差σ2与试验所需总体样本容量N的关系,并与传统的试验设计方法作比较(见表2)。结果表明,自适应两阶段设计方法明显优于传统的试验设计方法,大大减少了试验所需样本容量。由此可见自适应两阶段设计方法在临床试验设计中有明显的伦理学价值和经济学价值。当然,本文仅仅讨论了平衡设计的问题,即假定每组试验设计所需的样本容量是相等的,对于非均衡设计的问题有待进一步的研究。
[1]Bischoff,W.,Miller,F.Adaptive Two-Stage Test Procedures to
Find the Best Treatment in Clinical Trials[J].Biometrika,2005,92.[2]Bretz,F.,Schmidli,Racine,A.,Maurer,W.Confirmatory Seam
less Phase II/III Clinical Trials with Hypotheses Selection at Interim:General Concepts[J].Biometrical J.,2006,48.
[3]Bechhofer,R.E.,Dunnett,C.W.,Sobel,M.A Two-Sample
Multiple Decision Procedure for Ranking Means of Normal Popu
lations with a Common Unknown Variance[J].Biometrika,1954,41.[4]Liu,Q.,Pledger,G.W.Phase II and III Combination Designs to Accelerate Drug Development[J].Amer.Statist.Assoc,2005,100.
[5]Maca,J.,Bhattacharya,S.,Dragalin,V.,Gallo,P.,Krams,M.Adaptive Seamless Phase II/III Designs– Background,Operational Aspects,and Examples[J].Drug Informat,2006,40.
[6]Miller,F.Variance Estimation in Clinical Studies with Interim Sample Size Reestimation[J].Biometrics,2005,61.
[7]Wang,J.An Adaptive Two-Stage Design with TreatmentSelection Using the ConditionalError Function Approach[J].Biometrical,2006,48.
(责任编辑/亦 民)
O212
A
1002-6487(2011)03-0021-02
言方荣(1978-),男,江苏常州人,研究方向:生物统计。
