(001)面任意方向单轴应变硅材料能带结构*

马建立 张鹤鸣 宋建军 王冠宇 王晓艳

(西安电子科技大学微电子学院，宽禁带半导体材料与器件教育部重点实验室，西安 710071)

(2010年5月15日收到;2010年6月4日收到修改稿)

(001)面任意方向单轴应变硅材料能带结构*

马建立1)†张鹤鸣 宋建军 王冠宇 王晓艳

(西安电子科技大学微电子学院，宽禁带半导体材料与器件教育部重点实验室，西安 710071)

(2010年5月15日收到;2010年6月4日收到修改稿)

首先计算了(001)晶面单轴应变张量，在此基础上采用结合形变势理论的K·P微扰法建立了在(001)晶面内受任意方向的单轴压/张应力作用时，应变硅材料的能带结构与应力(类型、大小)及晶向的关系模型，进而分析了不同单轴应力(类型、大小)及晶向对应变硅材料导带带边、价带带边、导带分裂能、价带分裂能、禁带宽度的影响.研究结果可为单轴应变硅器件应力及晶向的选择设计提供理论依据.

单轴应变硅，K·P法，能带结构

PACS:71.15.－ m，71.70.Fk

1.引 言

应变硅由于具有载流子迁移率高、能带结构可调、并与硅的微电子技术相兼容等优异特性，成为提高器件与电路性能的首选方案［1］.在硅中引入应变的方法常见有衬底致双轴应变和工艺致单轴应变.与双轴应变相比，单轴应变以其在低应变和高垂直电场下可以更大程度地改善P-MOSFET(p-type metal-oxide-semi-conductor field-effect transistors)的性能，且工艺比双轴应变更容易实现等优点，而成为当今应变硅技术的主流.

应变硅器件和电路性能的增强主要得益于沟道中引入应力后诱导材料能带结构发生变化，进而使得载流子迁移率得到提高.研究表明:应变硅材料载流子迁移率不仅与应力(类型、大小)有关，还与衬底晶向密切相关［2］.因此，深入研究不同应力(类型、大小)及衬底晶向作用下应变硅材料的能带结构，对应变硅MOSFET器件导电沟道应力与晶向的合理选择，进而获得高载流子迁移率的应变材料，提高器件与电路性能具有重要的理论意义和应用价值.

目前，国外对应变硅的研究基本上集中在反型层及器件载流子输运、新型器件结构及其优化等方面，而针对应变硅材料能带结构的研究相对较少［3—5］.国内近年来在硅基双轴应变材料的能带结构方面开展了一些工作［6—9］，但对于单轴应力作用下应变硅材料能带结构的研究鲜有报道，理论研究滞后于应用研究.本文基于理论框架［10］，结合形变势理论，建立了在(001)晶面内受任意方向的单轴压/张应力作用时，应变硅材料的能带结构与应力(类型、大小)及晶向的关系模型，分析了不同单轴压/张应力作用下应变硅材料能带结构随晶向的变化情况.

2.能带模型

2.1.(001)晶面单轴应变张量计算

如图(1)所示，主晶轴坐标系为(x，y，z)，所施外力 T 为(001)面内任意方向的力，坐标系(x′，y′，z′)的 z′轴垂直于(001)面，x′轴沿着外力 T 所在的方向.在坐标系(x′，y′，z′)内，应力张量可表示为

为将应力张量 T′从坐标系(x′，y′，z′)转换到主晶轴坐标系(x，y，z)，需要一转变矩阵U，

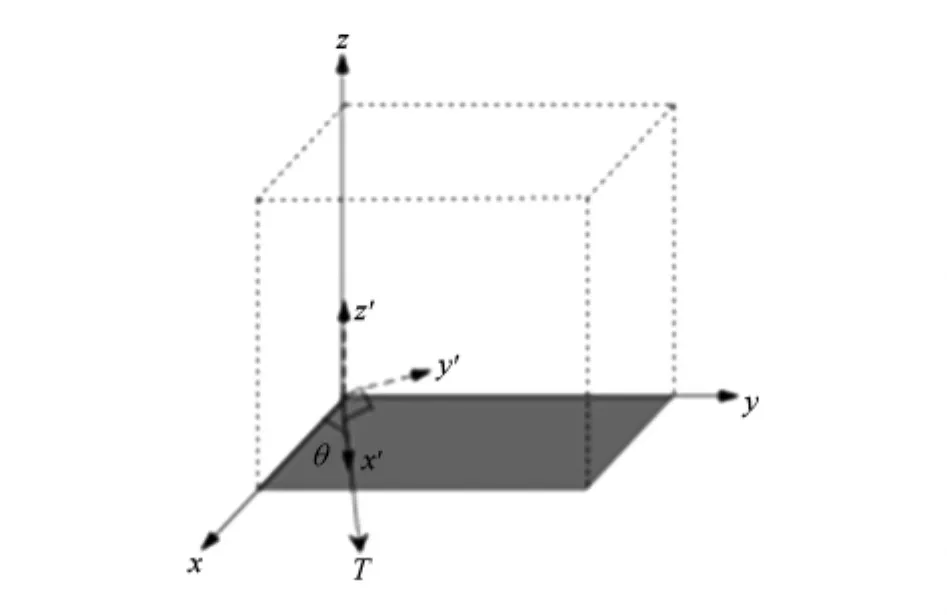
图1 (001)面单轴应变张量计算示意图

其中θ为方位角，即为x′轴与x轴的夹角.其具体转换公式为

式中 i，j，k 分别代表 x，y，z方向.

在弹性限度范围内由胡克定律知，应变张量与应力存在如下关系

式中sijkl为体硅材料的弹性顺度系数，具体数值见表1.

由(3)，(4)式即得在(001)晶面内受单轴应力作用时，应变Si材料单轴应变张量:

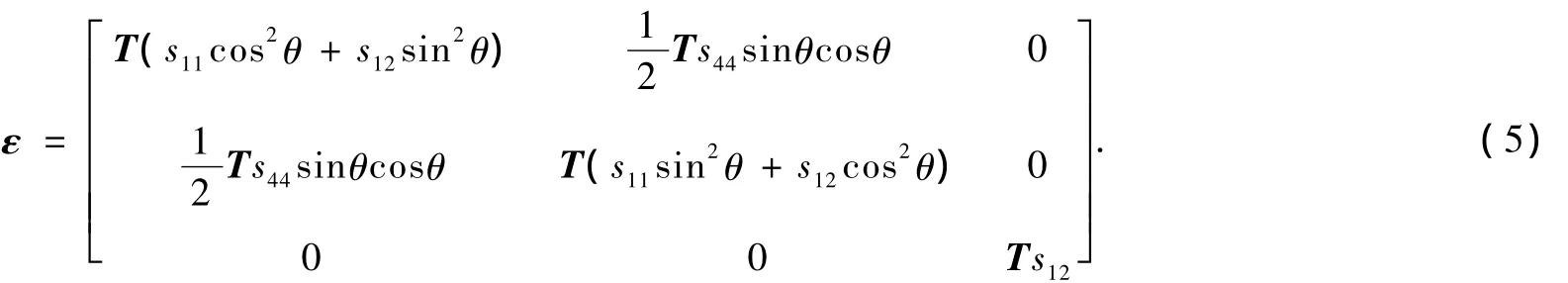
表1 导带、价带模型计算所用物理参数

2.2.导带模型

在体硅中，导带的极值在沿Δ轴方向(［100］方向)从布里渊区中心到布里渊区边界的0.85倍处，导带底是六度简并的Δ能谷(见图2(a)).在(001)面单轴应力作用下，原本简并的导带能级将发生分裂(见图2(b)).外加应力对硅材料导带边能级的移动可用形变势理论来描述［13］.具体计算公式为

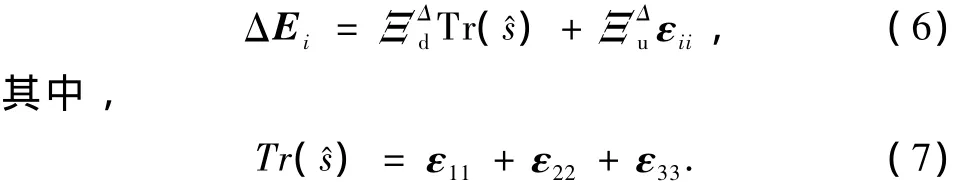
在单轴应力作用下应变硅材料导带底能级能量可表示为

将(6)，(7)式代入(8)式即可确定在单轴应力作用下应变硅材料导带底的能量.

2.3.价带模型

K·P微扰法是计算半导体材料在导带底和价带顶极值附近能带结构的一种有效方法，它能给出晶体在一些特殊对称点附近能带结构的全部信息.考虑到器件建模与仿真中需要用到应变硅材料价带带边(即k=0的Γ点处)参数模型，采用结合形变势理论的六能带 K·P微扰法，同时考虑自旋-轨道耦合效应求解Γ点处的薛定谔方程，通过价带形变势理论引入应变对能带结构的影响.薛定谔方程如下:

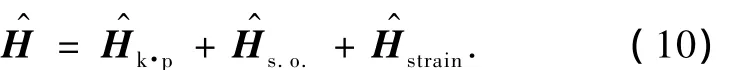
3.结果与讨论

图3为单轴不同压/张应力作用下导带底能量随应力方向的变化情况.从图可见，未受应力作用时，体硅导带底附近能谷是六度简并的(图3(b))，当有单轴应力作用时，简并被部分或全部消除.在1 GPa大小的单轴压应力作用下(见图3(a))，应力沿［100］方向作用时，导带底附近能谷分裂为一组二度简并的能谷和一组四度简并的能谷，其中二度简并能谷(沿(［100］与方向能谷)由于能量较低而成为导带带边;当所施应力由［100］方向变化到［110］方向时，能谷分裂为三组二度简并的能谷，此时，沿［100］与方向的能谷仍为导带带边;在应力方向为［110］方向时，能谷分裂为一组二度简并的能谷和一组四度简并的能谷，但这时四度简并的能谷(沿方向能谷)能量较低而成为导带带边;在应力方向由［110］变化到［010］时，能谷又分裂为三组二度简并的能谷，沿 ［010］与方向的能谷为导带带边;当应力方向变化到［010］方向时，三组二度简并的能谷重新又分裂为一组二度简并的能谷和一组四度简并的能谷，导带带边为二度简并的能谷(沿［010］，方向能谷).

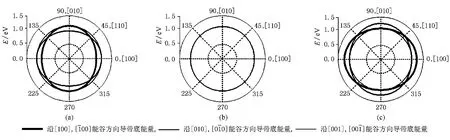
在1 GPa大小的张应力作用下(见图3(c))，在应力方向由［100］晶向变化到［010］晶向的过程中，导带底附近能谷的简并情况与压应力作用时的相同，不同的是当应力沿［100］方向时导带带边为四度简并的沿［010］，，［001］，方向的能谷，在应力方向由［100］晶向一直变化到［010］晶向的过程中，导带带边为二度简并的沿［001］，方向的能谷，当应力方向在［010］晶向时，这时导带带边又变为四度简并的方向沿［100］，，［001］，的能谷.(001)面其余方向施力时的能带简并分裂情况同上分析.

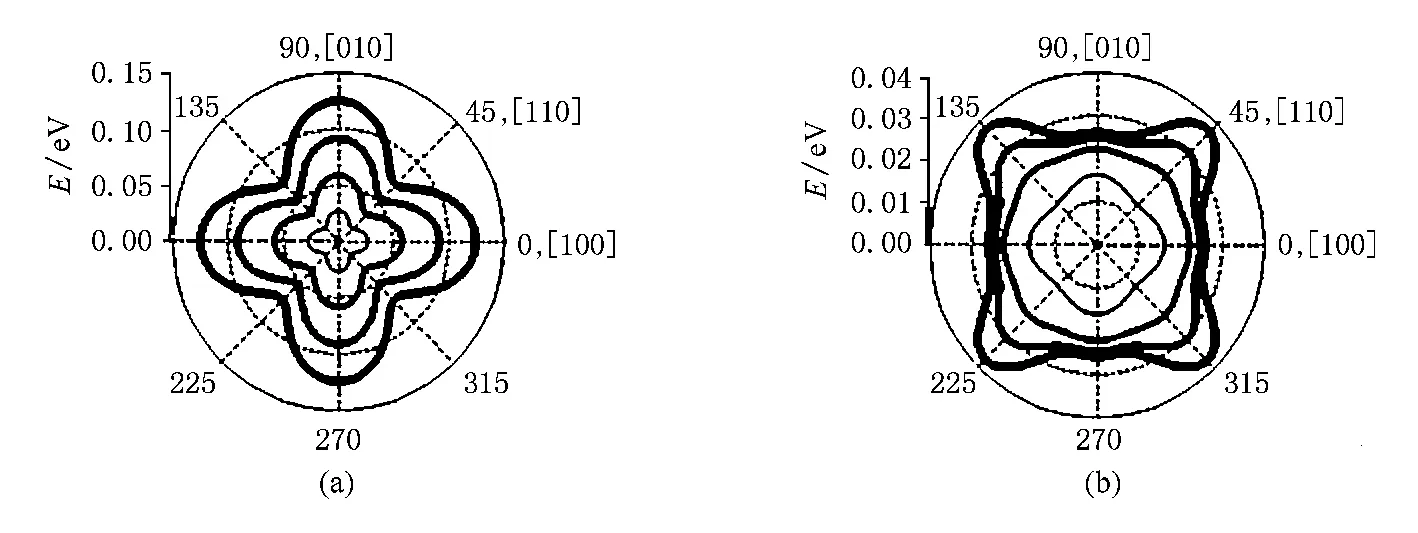
图4(a)为不同单轴压应力作用下导带分裂能随应力方向的变化情况.为避免重复，图中只给出所施应力方向由［100］方向变化到［010］方向时的情况.从图可知，当应力沿同一晶向作用时，导带分裂能随应力的增大而增大(图中线条越粗表示所施加的应力越大).在一定的应力作用下，当应力方向在(001)面内由［100］晶向逆时针变化到［010］晶向的过程中，应变硅材料的导带分裂能呈现出先减小后增大的趋势，且关于［110］晶向成轴对称分布，所施应力方向沿［110］晶向时，导带分裂能最小.不同单轴张应力作用下导带分裂能随应力方向的变化情况见图4(b)，其变化情况与压应力的相同.

图4 (001)面任意方向单轴应变硅材料导带分裂能随应力的变化情况 (a)单轴压应变(T=－2，－1.5，－1.0，－0.5，0 GPa)，(b)单轴张应变(T=0，0.5，1.0，1.5，2.0 GPa)

单轴不同压/张应力作用下价带Γ点处能量随应力方向的变化情况见图5.未受应力作用时，体硅材料价带的极值处于Γ点处计及，K·P项和自旋-轨道耦合效应，其能带由四度简并的Γ8能带(j=3/2，称为重空穴带和轻空穴带)以及二度简并的 Γ7能带(j=1/2，自旋-轨道裂开带)组成(见图5(b)所示)，Γ8与 Γ7能带之间裂距为 Δ(具体数值见表1).在1 GPa的单轴压应力作用下(见图5(a))，原来四度简并的Γ8能带在(001)面内的所有晶向均分裂为一组二度简并的能带(称为价带带边，与未应变的重空穴带对应)和一组二度简并的能带(称为亚带带边，与未应变的轻空穴带对应).且能带在能带的上方，自旋-轨道裂距较未应变时的有所增大;而在1 GPa的单轴张应力作用下(见图 5(c))，虽然张应变使得能带与能带在(001)面内的所有晶向均分裂，但能带在能带的下方，且自旋-轨道裂距在应力接近［110］晶向时比未应变时的有所降低.

单轴不同压/张应力作用下Γ点处价带分裂能随应力方向的变化情况可从图5中提取数据获得(见图6).当应力沿同一晶向作用时，价带分裂能随应力大小的增大而增大(图中线条越粗表示所施加的应力越大).在一定大小的单轴应力作用下，对压应变来说，应力方向在［110］晶向时，价带分裂能最小，方向在［100］及［010］向时，价带分裂能最大(见图6(a)).而对张应变来说，应力方向在［110］晶向时，价带分裂能最大，方向在［100］及［010］晶向时，价带分裂能相对较小(见图6(b)).在同样大小的应力沿同一晶向作用时，压应变下产生的价带分裂能大于张应变产生的价带分裂能.

禁带宽度是半导体材料中一个重要的物理参数，其大小的确定对于材料、器件设计至关重要.图7示出了单轴不同压/张应力作用下禁带宽度(导带带变能级与价带带变能级之差)随应力方向的变化情况.由图可见:当所施加的应力其方向在(001)面内由［100］晶向逆时针变化到［010］晶向的过程中，在所有晶向中，禁带宽度随所施加应力的大小增大而减小(图中箭头线所指方向为应力大小增大的方向)，这与双轴应变下禁带宽度随应力大小的变化情况相同［7］.在一定大小的单轴应力作用下，单轴压应力沿［110］方向作用时禁带宽度出现最大值，而单轴张应力下的禁带宽度随应力方向变化不明显.

图7 (001)面任意方向单轴应力对硅材料禁带宽度的影响 (a)单轴压应变(T=－2，－1.5，－1.0，－0.5，0 GPa)，(b)单轴张应变(T=0，0.5，1.0，1.5，2.0 GPa)

4.结 论

本文计算了(001)晶面单轴应变张量，建立了当硅材料在(001)晶面内受任意方向的单轴压/张应力作用时，应变硅材料的能带结构与应力(类型、大小)及晶向的关系模型，并从中提取出导带分裂能、价带分裂能、禁带宽度相关参数.结果表明:

1)在不同单轴压/张应力作用下，导带、价带的简并被部分或全部消除;

2)所施加的单轴应力其方向在(001)面内由［100］晶向逆时针变化到［010］晶向的过程中，在所有晶向中，导带分裂能、价带分裂能随应力大小的增大而增大，禁带宽度随应力大小的增大而减小;在同样大小的应力沿同一晶向作用时，压应变下产生的价带分裂能大于张应变产生的，而导带分裂能在压应变下产生的和张应变的基本相同.

［1］Song J J，Zhang H M，Dai X Y，Hu H Y，Xuan R X 2010Acta Phys.Sin.59 580(in Chinese)［宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜2010物理学报59 580］

［2］Sun G Y，Sun Y K，Nishida T，Thompson S E 2007Appl.Phys.Lett.102 084501

［3］Fischetti M V，Ren Z，Solomon P M，Yang M，Rim K 2003J.Appl.Phys.94 1079

［4］Phama A T，Jungemann C，Meinerzhagen B 2008Solid-State Electronics52 1437

［5］Ungersboeck E，Dhar S，Karlowatz G，Sverdlov V，Kosina H，Selberherr S 2007IEEE Trans.on Electron Dev.54 2183

［6］Song J J，Zhang H M，Hu H Y，Dai X Y，Xuan R X 2007Chin.Phys.16 3827

［7］Song J J，Zhang H M，Dai X Y，Hu H Y，Xuan R X 2009Acta Phys.Sin.58 7947(in Chinese)［宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜2009物理学报58 7947］

［8］Cheng B W，Yao F，Xue C L，Zhang J G，Li C B，Mao R W，ZuoY H，Luo L P，Wang Q M 2005Acta Phys.Sin.54 4350(in Chinese)［成步文、姚 飞、薛春来、张建国、李传波、毛容伟、左玉华、罗丽萍、王启明2005物理学报54 4350］

［9］Song J J，Zhang H M，Dai X Y，Hu H Y，Xuan R X 2008Acta Phys.Sin.57 7228(in Chinese)［宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜2008物理学报57 7228］

［10］Xie X D，Lu D 1998Energy Band Theory of Solids(Shangai:Fuda University Press)p58(in Chinese)［谢希德、陆 栋1998固体能带理论(上海:复旦大学出版社)第58页］

［11］Madelung O 2003Semiconductors:Data Handbook，Data in Science and Technology(3rd ed)(German:Springer Press)p16

［12］Kasper E 2002PropertiesofStrainedandRelaxedSilicon Germanium(Beijing:National Defense Industry Press)p114

［13］Smirnov S，Kosina H 2004Solid-State Electronics48 1325

［14］Manku T，Nathan A 1993J.Appl.Phys.73 1205

PACS:71.15.－ m，71.70.Fk

Energy band structure of uniaxial-strained silicon material on the(001)surface arbitrary orientation*

Ma Jian-Li†Zhang He-Ming Song Jian-Jun Wang Guan-Yu Wang Xiao-Yan
(Key Laboratory of Ministry of Education for Wide Band-Gap Semiconductor Materials and Devices，School of Microelectronics，Xidian University，Xi’an 710071，China)
(Received 15 May 2010;revised manuscript received 4 June 2010)

The strain tensor arising from uniaxial stress along an arbitrary direction on the(001)surface of Si is calculated.With these uniaxial strain tensor，the band structure of silicon material under arbitrary uniaxial stress on the(001)surface is calculated using K·P perturbation theory coupled with linear deformation potential theory.The relation between energy band structure and stress parameters(type，direction，magnitude)was obtained.Finally，the uniaxial stress induced band structure change，such as that of the conduction band(CB)and the valence band(VB)edge levels，CB and VB splitting energy and the bandgap is demonstrated.Results of these band structure can be used as a guide for the design and the selection of the optimum strain and crystal orientation configuration of uniaxial strained silicon devices.

uniaxial strained silicon，K·P method，energy band structure

*国家部委项目(批准号:51308040203，6139801)，中央高校基本科研业务费项目(批准号:72105499)和陕西省自然科学基础研究计划(批准号:2010JQ8008)资助的课题.

*Project supported by the National Ministries and Commissions of China(Grant Nos.51308040203，6139801)，the Fundamental Research Funds for the Central Universities of China(Grant No.72105499)and the Natural Science Basic Research Plan in Shaanxi Province of China(Grant No.2010JQ8008).