横磁模式下二维非磁化等离子体光子晶体的线缺陷特性研究*

章海锋 刘少斌 孔祥鲲

1)(南京航空航天大学信息科学与技术学院，南京 210016)

2)(中国人民解放军炮兵学院南京分院，南京 211132)

3)(镇江船艇学院，镇江 212003)

(2010年7月18日收到;2010年8月6日收到修改稿)

横磁模式下二维非磁化等离子体光子晶体的线缺陷特性研究*

章海锋1)2)刘少斌1)†孔祥鲲1)3)

1)(南京航空航天大学信息科学与技术学院，南京 210016)

2)(中国人民解放军炮兵学院南京分院，南京 211132)

3)(镇江船艇学院，镇江 212003)

(2010年7月18日收到;2010年8月6日收到修改稿)

采用等离子体的分段线性电流密度卷积时域有限差分算法研究了横磁波入射时具有单一线缺陷的二维非磁化等离子体光子晶体的缺陷模特性.从频域角度分析得到微分高斯脉冲的透射系数，并讨论该光子晶体的晶格常数、介质圆柱半径、周期常数、缺陷层参数和等离子体参数对缺陷模特性的影响.结果表明，改变周期常数、缺陷层位置和等离子体碰撞频率不会改变缺陷模的频率，改变缺陷层介质圆柱的相对介电常数、半径和缺陷层到介质层的中心距离可以在不改变禁带宽度的前提下实现对缺陷模的调节，改变晶格常数、介质圆柱半径和等离子体频率能同时实现对禁带宽度和缺陷模的调节.

等离子体，光子晶体，缺陷模，时域有限差分算法

PACS:52.77.－ j，42.40.－ w，52.65.－ y，52.27.Lw

1.引 言

光子晶体是由折射率不同的介质在空间交迭而成 的 一 种 周 期 性 结 构，最 早 由 John［1］和Yablonovitch［2］等提出，人们根据空间分布的不同将光子晶体划分为一维、二维和三维光子晶体.光波在光子晶体中传播时受到周期性的散射和衍射作用，使得光子晶体具有一定的光子禁带隙，即频率落在带隙中的电磁波禁止传播.当光子晶体引入缺陷后，破坏了原有光子晶体的周期性和对称性，光子禁带中就会出现频带较窄的缺陷模.这些特性使得光子晶体具有十分广泛的应用前景［3—9］.等离子体光子晶体的概念是由 Hojo和 Mase［10］提出的，它是一种由等离子体和其他介质组成的光子晶体.等离子体是一种具有耗散和色散特性的介质，它的折射率由入射波频率决定，这使等离子体光子晶体具有一些特殊的禁带特性［11，12］.另一方面等离子体的物理特性可以通过外磁场和等离子体密度和碰撞频率等参数控制，这给禁带的调制带来了便利.因此等离子体光子晶体已经成为国内外学者研究的热点.目前，大量的研究工作集中在一维等离子体光子晶体禁带和缺陷模的特性上.Hojo和 Mase［13］对电磁波在一维非磁化等离子体中的传播特性进行了研究，指出电磁波传播模式主要由等离子体密度决定.Shiveshwair和 Mahto［14］对等离子体光子晶体的滤波特性进行了研究，指出改变等离子体密度和等离子体层的厚度可以实现对禁带的调节.Li等［15］通过对色散关系的计算得到了明显的通带和禁带，得出了等离子体光子晶体的色散规律.刘少斌等［16，17］对一维等离子体光子晶体的缺陷模特性进行了研究，指出无论是磁化还是非磁化的条件下，都可以通过引入缺陷层实现光子局域态，并且通过改变等离子体参数实现了光子晶体的可调谐滤波.对二维等离子体光子晶体的工作主要集中在色散特性的研究和实验验证上.亓丽梅等［18，19］对二维磁化和非磁化等离子体光子晶体的色散特性进行了研究，指出改变外磁场和等离子体参数可以实现对色散特性的调整.Sakai等［20］用实验方法验证了二维等离子体光子晶体的禁带特性并对电磁波的传播现象给出了新的模型和解释.而关于二维等离子体光子晶体缺陷模的理论研究还不够深入.在工程上人们可以将含有线缺陷的二维非磁化等离子体光子晶体制成可调谐滤波器、功分器、耦合腔体和波导等微波器件.因此研究二维非磁化等离子体光子晶体的缺陷模特性很有价值.

本文以微分高斯脉冲为激励源，在理想情况下用等离子体的分段线性电流密度卷积时域有限差分(PLCDRC-FDTD)算法［21，22］对横磁(TM)波在具有单一线缺陷的二维非磁化等离子体光子晶体中的传播进行了仿真.缺陷模特性由仿真计算得到的透射系数获得.然后以晶格常数、介质圆柱半径、周期常数、等离子体参数和缺陷层参数为参量对缺陷模特性进行了分析.

2.数值计算方法

时域有限差分(FDTD)法是一种计算精度很高的数值方法，计算过程考虑了所有的电磁损耗，且十分适用于对复杂结构和多介质电磁问题的计算.PLCDRC-FDTD算法具有很高的计算精度，特别适用于对色散介质的计算.计算过程中用到的电场和卷积项的迭代公式如下:

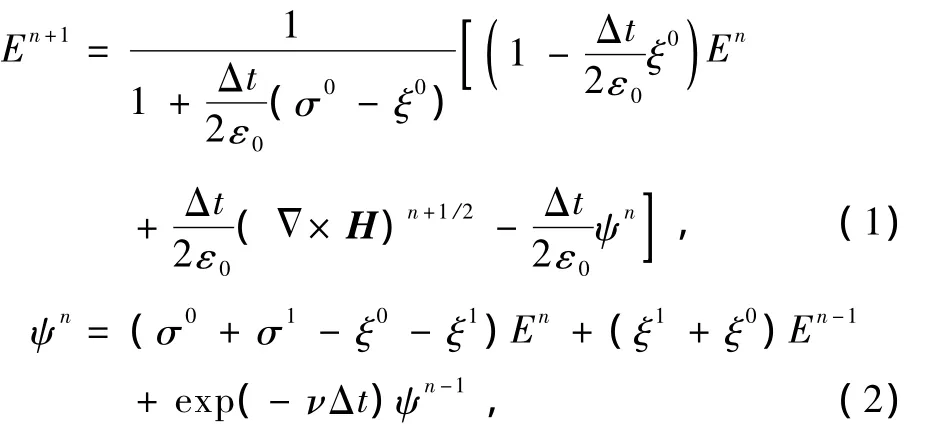
式中各参量定义详见文献［22］.等离子体磁场迭代方程以及电介质部分电场和磁场的迭代公式与常规FDTD算法相同.

3.数值计算的参数与物理模型

图1给出了仿真计算的物理模型，在等离子体中排列着周期分布的介质圆柱，栅格为正方形.线缺陷层是沿+y轴方向填充介质圆柱.所有的介质圆柱在z轴方向上为无限长，TM波沿+x轴入射，其频率范围取0—30 GHz.用a表示晶格常数，b表示缺陷层到介质层的中心距离，N表示该光子晶体的周期常数，M表示缺陷层在该光子晶体中的位置.R为介质圆柱的半径，r为缺陷层介质圆柱的半径.仿真计算的初始参数设定如下:周期常数N=10，介质圆柱的半径R=2.5 mm，晶体格常数a=10 mm，介质圆柱的相对介电常数ε1=7，缺陷层位置参数M=6，缺陷层介质圆柱的半径 r=2.5 mm，常数b=10 mm，缺陷层介质圆柱的相对介电常数ε2=4.5，等离子体频率ωp=4.8π×109rad/s，等离子体碰撞频率ν=2.7×109rad/s.

根据Courant稳定性条件，用220×220个计算网格来剖分大小为110 mm×110 mm的光子晶体，用于计算的空间步长取0.5 mm，时间步长取1 ps.吸收边界采用完全匹配层，占据5个网格，分布在计算空间的四周.沿+x轴传播的入射电磁波为微分高斯脉冲，该脉冲的表达式如下:

式中取常量A=4.67 V/m，τ=20.入射波的高频分量越多τ值越小.整个计算时间进行10000步.通过傅里叶变换将得到的电场分量由时域转换到频域来求透射系数，再用透射系数的频谱来表征缺陷模.图2给出了缺陷层介质圆柱的相对介电常数ε2分别取2，4.5，7，11的透射系数频谱.由图2可知，二维非磁化等离子体光子晶体含有单一线缺陷时禁带中存在着明显的缺陷模.下面就以晶格常数、介质圆柱半径、周期常数、等离子体参数和缺陷层参数为参量对其缺陷模特性进行讨论.

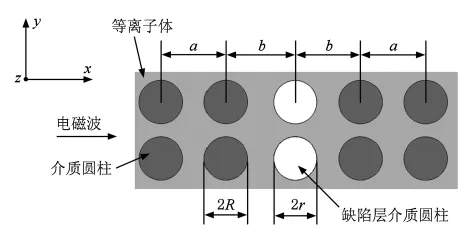
图1 仿真计算的物理模型

4.计算结果与讨论

4.1.ε2对缺陷模的影响

图3给出了ε2取值1—14的三维透射系数频谱.由图2和图3可知，二维非磁化等离子体光子晶体引入线缺陷后，禁带中将会出现较为明显的单模缺陷.禁带宽度不会发生明显变化，但是透射系数峰值将会发生较为明显的变化.缺陷层介质圆柱的相对介电常数ε2由1变化到14的过程中，缺陷模频率先向低频方向移动，缺陷模透射峰值逐渐增大，当ε2增加到7时，缺陷模将会和禁带的下边带重合，此时缺陷模消失.再继续增大ε2，在禁带的上边带将产生一个新的缺陷，进一步增大 ε2的值，缺陷模将向低频方向移动，逐渐靠近禁带中心，缺陷模透射峰值也将随之逐渐减小.缺陷模的移动呈现周期性变化，因此可以通过改变ε2使得缺陷模频率涵盖禁带所有频率，给设计带通滤波器带来了便利.另一方面，缺陷模频率几乎与 ε2呈线性变化，所以可以通过这一性质实现对缺陷层介质的相对介电常数的测量，使得含线缺陷的二维非磁化光子晶体有了更为广阔的应用前景.

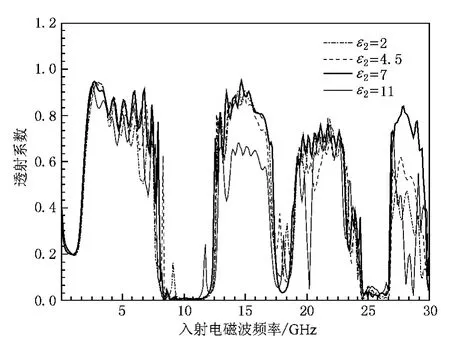
图 2 ε2=2，4.5，7，11 的透射系数频谱

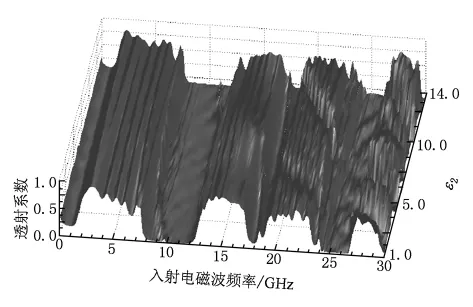
图3 ε2取值1—14时的三维透射系数频谱

4.2.周期常数和缺陷层位置对缺陷模的影响

图4给出了周期常数 N分别取9，11，15，20的透射系数频谱.由图4可知，周期常数N对禁带带宽无影响.缺陷模频率几乎不会随着N的增大而发生改变，但是缺陷模透射峰值会随着N的增大逐渐减小.当N等于20时，此时禁带中的缺陷模已经完全消失.这是因为缺陷模的产生主要源于缺陷层介质圆柱对入射电磁波的反射、散射和耦合作用，当缺陷层介质圆柱反射和散射的电磁波和行进中的电磁波发生干涉时，导致电磁能发生汇聚而在禁带中出现缺陷模.另外等离子体本身又是一种耗散性介质，电磁波在其中传播时电磁波的一部分能量将转换成为等离子体的内能.周期常数N越大意味着对缺陷模的衰减作用越强，因此缺陷模透射峰会随着N的增大而减小.图5为缺陷层位置参数M分别取 2，3，4，5，6，7，8，9，10 的透射系数频谱. 由图 5可知，缺陷模频率大小与参数M无关，参数M只会影响缺陷模透射峰值的大小.线缺陷对周期性和对称性破坏越大，入射波在缺陷层中的谐振和耦合作用就越强，缺陷模透射峰值就越大.因此 M=6时缺陷透射峰值最大.综上所述，增加周期常数N和改变缺陷层位置M只会影响缺陷模峰值的大小而不能改变缺陷模频率.

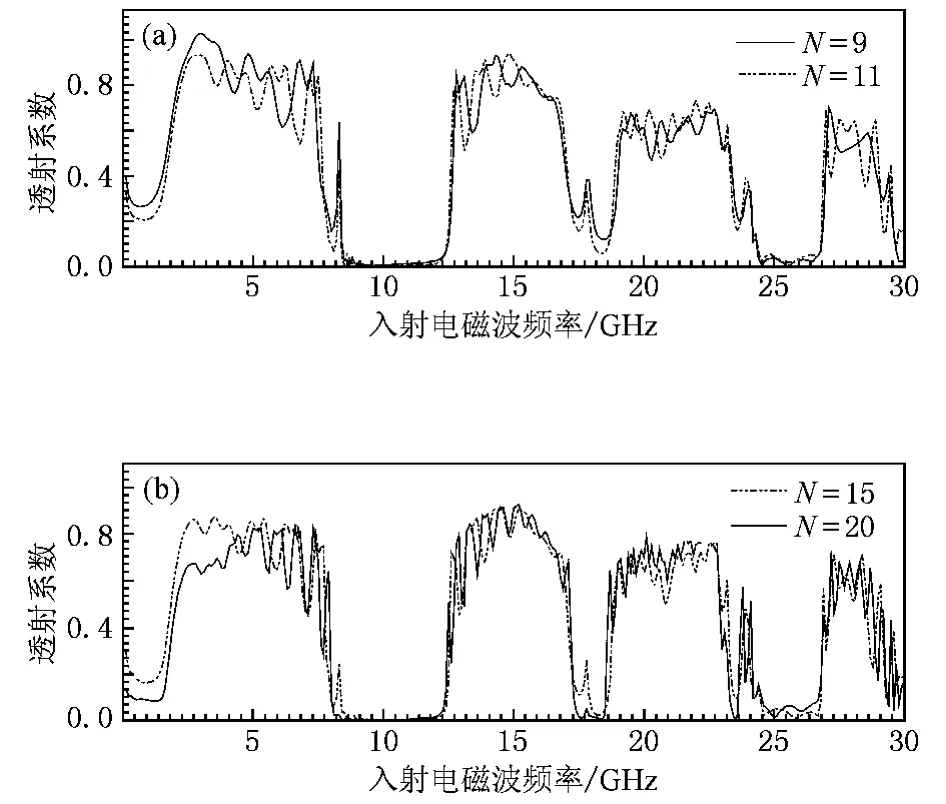
图4 不同周期常数的透射系数频谱 (a)N=9，11，(b)N=15，20

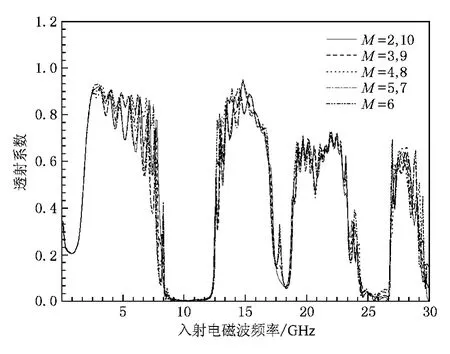
图 5 M=2，3，4，5，6，7，8，9，10 的透射系数频谱

4.3.R和a对缺陷模的影响

图6给出了介质圆柱半径 R分别等于1，2.5，3.5，5 mm的透射系数频谱，图7给出了介质圆柱半径R=0.5—5 mm的三维透射系数频谱.由图6和图7可知，光子禁带的带宽会随着R的增大而逐渐减小，禁带的中心频率向低频方向移动.同时缺陷模频率也将向低频方向移动，缺陷模透射峰值逐渐减小.当R增大到a/2时，已不存在光子禁带和缺陷模.这是因为当R=a/2时彼此相邻的介质圆柱已经相切，此时的光子晶体已变成用非磁化等离子体填充相对介电常数为ε1的介质构成的二维光子晶体.介质背景的介电常数相对等离子体来说较大，此时在TM模式下光子晶体不会有明显的禁带，自然缺陷模也不存在.图8给出了晶格常数a分别等于9，10，14，15 mm 的透射系数频谱，图 9给出了晶格常数a取值5—15 mm的三维透射系数频谱.由图8和图9可知，光子禁带的带宽会随着a的增大而逐渐减小，禁带的中心频率向低频方向移动，光子禁带的数目将逐渐减少.缺陷模将会随着a的增大而向低频方向移动，缺陷模透射峰值逐渐减小，直至最后完全消失.改变R和a的大小实质上是改变填充率f(f=πR2/a2)的大小.改变R时，填充率 f的变化范围是［0.009，0.785］，改变 a时，填充率f的变化范围是［0.087，0.785］.如果填充率取值较大，如f≥0.785时，等离子体光子晶体的性质将发生变化，此时在TM模式下不能产生光子禁带和缺陷模.如果填充率取值较小，如f∈［0.009，0.089］时，等离子体光子晶体产生的禁带中不存在缺陷模，因为此时填充的介质圆柱对入射电磁波的反射、散射和耦合作用较弱，入射电磁波能量大部分已经被等离子体吸收，很难在缺陷层中谐振出较为明显的缺陷模.

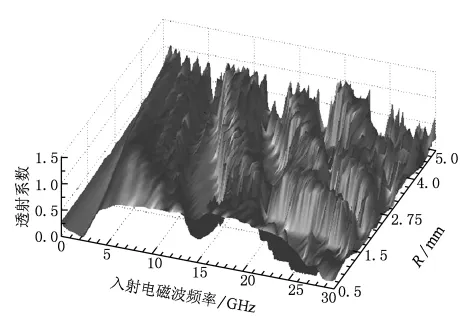
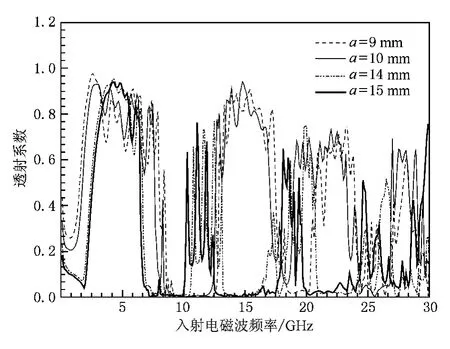
图 8 a=9，10，14，15 mm 的透射系数频谱

综上所述，要产生明显的缺陷模，等离子体光子晶体的填充率最小应满足 f∈［0.158，0.240］，此时减小R和a的大小可以实现对禁带的拓展，禁带的中心频率向高频方向移动.在禁带中有明显的缺陷模，且缺陷模频率向高频方向移动，缺陷模透射峰值也将同时增大.在填充率一定的情况下，改变介质圆柱半径R和晶格常数a的大小，可以在拓展禁带带宽的同时实现对缺陷模频率和透射峰值的调整.

4.4.r和b对缺陷模的影响

图10给出了缺陷层介质圆柱半径r分别等于2，2.5，3.5，4 mm 的透射系数频谱，图 11给出了缺陷层介质圆柱半径r取值1—5 mm的三维透射系数频谱.由图10和图11可知，改变 r的大小，对禁带带宽几乎没有影响，只对透射系数峰值有影响，禁带中会出现较为明显的缺陷模.缺陷模频率将随着r的增大，先向低频方向移动，当 r增加到一定值时，缺陷模与禁带下边带重合，此时缺陷模消失.再继续增大r，在禁带的上边带将出现一个新的缺陷模，同时随着 r的增大向低频方向移动.缺陷模透射峰值大小是随着r的增大先增大后减小.这是因为电磁波通过缺陷层时受到介质圆柱反射和散射作用而发生谐振，而这种电磁波的谐振作用将汇聚很高的电磁能，因此会隧穿出缺陷而透过光子晶体.r的增大意味着缺陷层介质圆柱和介质层介质圆柱间的相干路径的增大，发生干涉的波长也随之增大，因而缺陷模的频率减小. 图 12 给出了 b分别等于 5，7.5，10，12，15 mm的透射系数频谱，图13给出了 b取值5—15 mm的三维透射系数频谱.由图12和图13可知，改变b的大小几乎不会影响禁带的宽度，禁带中存在明显的缺陷模，缺陷模频率随着b的增大而向低频方向移动，当b增大到一定值时，缺陷模将隐入禁带的下边带，并且在禁带上边带产生一个新的缺陷模，再继续增加b值，缺陷模频率将向低频方向移动.透射峰值随着b的增大先逐渐减小然后逐渐增大，最后再逐渐减小.这主要是源于缺陷层的介质圆柱对电磁能量的耦合作用.当b较小，如b等于5 mm时，缺陷层和介质层的圆柱相切，电磁能量主要以耦合的形式通过缺陷层，但是随着b的增大缺陷层对能量的耦合作用将逐渐减小，所以缺陷模透射峰值表现为逐渐减小，但是当b增大到一定值时，电磁波将会在缺陷层圆柱的反射和散射作用下而发生谐振，缺陷层对电磁能量的耦合作用将变得很小，缺陷层可等效为一个谐振腔，而电磁能量会因为谐振作用而汇聚，表现为缺陷模的透射峰值逐渐增大，如果再继续增加 b，等离子体对电磁能量的耗散作用将变大，电磁能量转化为等离子体的内能，表现为缺陷模透射峰值的减小.综上所述，可以根据入射电磁波的频率选择合适的r和b值来获得特定的缺陷模.

图10 不同缺陷及介质圆柱半径的透射系数频谱 (a)r=2，2.5 mm，(b)r=3.5，4 mm

图11 r取值1—5 mm的三维透射系数频谱

图12 不同中心距离的透射系数频谱 (a)b=5，7.5 mm;(b)b=10，12，15 mm

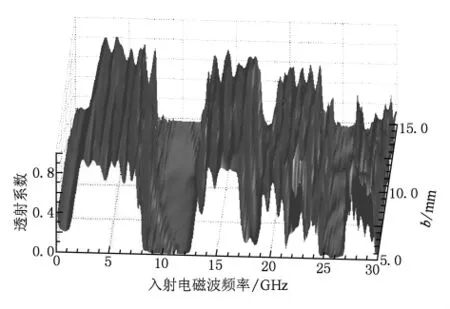
图13 b取值5—15 mm的三维透射系数频谱

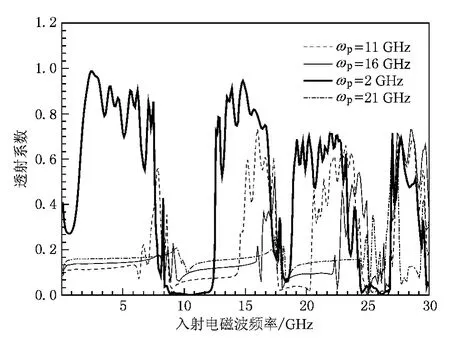
图 14 ωp=2，11，16，21 GHz的透射系数频谱

4.5.等离子体参数对缺陷模的影响

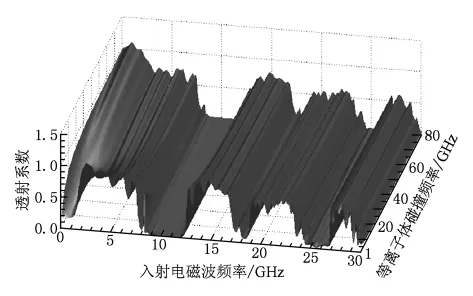
图 14 给出了等离子体频率 ωp=2，11，16，21 GHz的透射系数频谱.图15给出了等离子体频率ωp取值1—35 GHz的三维透射系数频谱.由图14和图15可知，等离子体频率对禁带和缺陷模有明显的调节作用，可以在实现改变禁带的同时实现对缺陷模的移动.等离子体频率越大缺陷模频率越高，缺陷模透射峰值越小，禁带带宽也越宽.如ωp=35 GHz时，禁带中已经不存在缺陷模.当缺陷模频率接近截止区［23，24］时，等离子体对缺陷模的衰减主要是共振衰减，这使得缺陷模透射峰值会有一个突然减小的过程.图16给出了等离子体碰撞频率ν=2，30，50，62 GHz的透射系数频谱.图17给出了等离子体碰撞频率ν取值1—80 GHz的三维透射系数频谱.由图16和图17可知，缺陷模频率不会随着等离子体碰撞频率的增加而改变，等离子体碰撞频率的改变只能调节缺陷模透射峰值的大小，即随着等离子体碰撞频率的增加缺陷模透射峰值先是减少然后增加最后趋于一个定值，这一点完全符合衰减常数与等离子体碰撞频率的关系［23，24］.

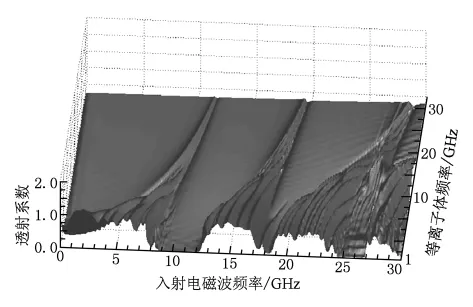
图15 等离子体频率ωp取值1—35 GHz的三维透射系数频谱

综上所述，改变等离子体频率不仅可以调节缺陷模频率和透射峰值的大小，同时也可以实现禁带拓展.调节等离子体碰撞频率的大小不能改变缺陷模频率的大小，仅能改变缺陷模透射峰值的大小.

5.结 论

本文以微分高斯脉冲为激励源，用等离子体的PLCDRC-FDTD算法对TM波在具有单一线缺陷的二维非磁化等离子体光子晶体中的传播进行了仿真计算.分析了晶格常数、介质圆柱半径、周期常数、等离子体参数和缺陷层参数对缺陷模特性的影响.计算结果表明:仅通过增加光子晶体的周期常数，改变线缺陷层的位置和增加等离子体碰撞频率不能改变缺陷模频率的大小，也不能实现缺陷模的移动，仅能改变缺陷模透射峰值大小.可以在不改变禁带宽度的前提下通过改变缺陷层介质圆柱的相对介电常数、半径和缺陷层到介质层的中心距离实现对缺陷模的频率和透射峰值的调节，其实质是调节电磁波在缺陷层中的耦合和谐振作用来实现对缺陷模的调节.改变晶格常数、介质圆柱的半径和等离子体频率可以在改变禁带宽度的同时实现对缺陷模频率和透射峰值的改变.但是当等离子体频率远远大于入射电磁波频率时，将不存在缺陷模.调节介质圆柱的半径和晶格常数的大小，实质上是调节填充率的大小，填充率设定在一定的范围内(如f∈［0.158，0.240］)时，可以通过改变R和a这两个参数来同时实现对禁带宽度和缺陷模的设定.上述分析表明，合理地选择介质圆柱的半径、晶格常数、周期常数、缺陷层参数和等离子体参数可以实现对缺陷模的调谐.

［1］John S 1987Phys.Rev.Lett.58 2486

［2］Yablonovitch E 1987Phys.Rev.Lett.58 2059

［3］Yakoyama H，Nishi K，Anan T 1992Opt.Quant.Electron.24 245

［4］Zhou W D，Sabarinathan J，Bhattacharya P，Kochman B，Berg E W，Yu P C，Pang S W 2001IEEE J.Quant.Electron.37 1153

［5］Villeneuve P R，Fan S，Joannopoulos J D 1996Phys.Rev.B 54 7837

［6］Feng T H，Dai Q F，Wu L J，Guo Q，Hu W，Lan S 2008Chin.Phys.B 17 4533

［7］Zhao X X，Zhu Q F，Zhang Y 2009Chin.Phys.B 18 2864

［8］Ma J Y，Liu S J，Zhang D W，Yao J K，Xu C，Jin Y X，Shao J D，Fan Z X 2008Chin.Phys.B 17 3704

［9］Fan S，Villeneuve P R，Joannopoulos J D 1997Phys.Rev.Lett.78 3294

［10］Hojo H，Mase A 2004J.Plasma Fusion Res.80 89

［11］Liu S B，Hong W，Yuan N C 2006Int.J.Infrar.Millim.Waves27 403

［12］Liu S B，Mo J J，Yuan N C 2005Acta Phys.Sin.54 2804(in Chinese)［刘少斌、莫锦军、袁乃昌2005物理学报54 2804］

［13］Hojo H，Mase A 2009J.Plasma Fusion Res.8 477

［14］Shiveshwari L，Mahto P 2006Solid State Communications138 160

［15］Li W，Gao H，Gong M L，Liu S G 2004Chin.Phys.13 1296

［16］Ma L，Zhang H F，Liu S B 2008Acta Phys.Sin.57 5089(in Chinese)［马 力、章海锋、刘少斌 2008物理学报57 5089］

［17］Zhang H F，Ma Li，Liu S B 2009Acta Phys.Sin.58 1071(in Chinese)［章海锋、马 力、刘少斌2009物理学报58 1071］

［18］Qi L M，Yang Z Q，Lan F，Gao X，Li D Z 2010Chin.Phys.B 19 034210

［19］Qi L M，Yang Z Q，Lan F，Gao X，Shi Z J，Liang Z 2010Acta Phys.Sin.59 0351(in Chinese)［亓丽梅、杨梓强、兰 峰、高 喜、史宗君、梁 正2010物理学报59 0351］

［20］Sakai O，Sakaguchi T，Tachibana K 2007Contrib.Plasma Phys.47 96

［21］Liu S B，Yuan N C，Mo J J 2003IEEE Microw.Wireless Compon.Lett.13 187

［22］Liu S B，Yuan N C，Liu S Q，Mo J J 2003IEEE Proc.Microw.Anten.Propag.152 189

［23］Zhuang Z W，Yuan N C，Liu S B，Mo J J 2005Plasma Stealth Technology(Beijing:Science Press)p13(in Chinese)［庄钊文、袁乃昌、刘少斌、莫锦军 2005等离子体隐身技术 (北京:科学出版社)第13页］

［24］Liu S B，Liu S，Hong W 2010Finite Difference Time Domain Method for Dispersive Media(Beijing:Science Press)p315(in Chinese)［刘少斌、刘 崧、洪 伟2010色散介质的时域有限差分算法(北京:科学出版社)第315页］

PACS:52.77.－ j，42.40.－ w，52.65.－ y，52.27.Lw

Defect mode properties of two-dimensional unmagnetized plasma photonic crystals with line-defect under transverse magnetic mode*

Zhang Hai-Feng1)2)Liu Shao-Bin1)†Kong Xiang-Kun1)3)
1)(College of Information Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)
2)(Nanjing Branch，Artillery Academy of the Chinese People，s Liberation Army，Nanjing 211132，China)
3)(Zhenjiang Watercraft Collegeg，Zhenjiang 212003，China)
(Received 18 July 2010;revised manuscript received 6 August 2010)

The piecewise linear current density recursive convolution finite-difference time-domain method of plasma is used to study the defect mode properties of transverse magnetic wave propagation in the two-dimensional unmagnetized plasma photonic crystals with a line-defect layer.In frequency domain，the transmission coefficients of electromagnetic differential Gaussian pulses are computed，and the effect of lattice constant，dielectric column radius，periodic constant，parameters of plasma and parameters of line-defect layer on defect mode properties of two-dimensional unmagnetized plasma photonic crystals are analyzed.The results illustrate that the frequency of defect mode cannot be tuned by changing periodic constant，position of the defect layer and plasma collision frequency，but be tuned by changing relative permittivity and radius of dielectric column in the defect layer，and central distance between defect layer and dielectric layer with the width of prohibit band gaps fixed.Furthermore，the defect mode and the width of prohibit band gaps can also be tuned by changing lattice constant，dielectric column radius and plasma frequency.

plasma，photonic crystals，defect mode，finite-difference time-domain method

*国家自然科学基金(批准号:60971122)和国家航空科学基金(批准号:2009ZA2008)资助的课题.

†通讯联系人.E-mail:lsb@nuaa.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.60971122)and the Aviation Science Foundation of China(Grant No.2009ZA2008).

†Corresponding author.E-mail:lsb@nuaa.edu.cn