基于 Gogny相互作用的非对称核物质同位旋的相关性质
2011-10-20杨艳芳陈列文
陈 融, 杨艳芳, 陈列文
(1.上海大学理学院,上海 200444;2.上海交通大学 物理系,上海 200240)
基于 Gogny相互作用的非对称核物质同位旋的相关性质
陈 融1,2, 杨艳芳1, 陈列文2
(1.上海大学理学院,上海 200444;2.上海交通大学 物理系,上海 200240)
基于有限程的 Gogny相互作用,系统研究同位旋非对称核物质的状态方程 (equation of state,EOS)及其单粒子势和它们的同位旋相关性.通过对比各类模型以及实验值,说明现有的 D1,D1S和 D1N这 3组 Gogny参数的不足之处,指出探寻新的 Gogny核力参数的必要性.
Gogny相互作用;非对称核物质;状态方程;同位旋
本工作研究的是零温均匀无穷大非对称核物质,该系统仅由中子和质子组成,且只考虑强相互作用.虽然在实际情况下,人们研究的往往是有限大核物质,但本研究依然可以根据均匀无穷大零温系统这个再考虑模型推导出的一系列物理量,结合表面能、库仑的相互作用等进行修正,进而给出和实验相吻合的结果.同时,很多真实的物理系统可以很好地看成是无穷大核物质,如中子星的内部、重原子核(如208Pb)内部等.
1 Gogny相互作用
Gogny两体相互作用的一般形式为[2]
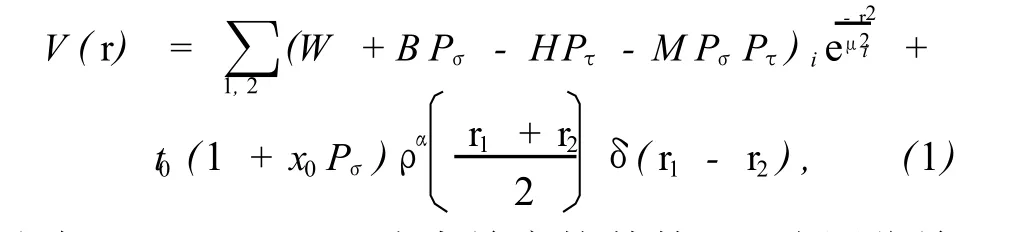
式中,r=r1-r2,Pσ为自旋交换算符,Pτ为同位旋交换算符.从式 (1)可以看到,Gogny相互作用由 11个含量纲参数 (W1,W2,B1,B2,H1,H2,M1,M2,μ1,μ2,t0)和 2个不含量纲的参数 (x0,α)共 13个参数构成 (此式省略了自旋轨道耦合项,因为该项不适用于均匀无穷大核物质).
文献[2-9]均未明确给出基于 Gogny相互作用的单粒子势和每核子能量的具体表达式.本研究给出了基于 Gogny相互作用的零温均匀无穷大非对称核物质的单粒子势和每核子能量的表达式,这对研究相关的物理量具有重要意义.同时,本工作也将系统地研究同位旋非对称核物质的状态方程和单粒子势及其同位旋相关性.
2 计算与分析
本研究根据已有的 3组 Gogny相互作用参数D1[2],D1S[10],D1N[11],并结合其他核力模型和实验数据,分析了非对称核物质中每核子能量随密度的变化关系、单粒子势随单核子能量的变化关系、对称势随核子动能的变化关系、等压压缩系数随同位旋不对称度的变化关系、有效质量的同位旋劈裂以及对称能随密度的变化关系等.此外,还计算了饱和密度处对称核物质性质以及对称能的高阶特征参数,讨论了等压不可压缩系数同位旋依赖的抛物线近似.本研究中所有的物理量均采用自然单位制.
2.1 每核子能量与对称能
每核子能量 E(ρ,δ)是在数密度为ρ=ρn+ρp,同位旋不对称度为δ=(ρn-ρp)/ρ的核物质中,平均每个核子的总能量.非对称核物质的状态方程(equation of state,EOS)就是每核子能量 E(ρ,δ)的表达式.基于 Gogny相互作用的 EOS为

式中 ,fτ=2h-3Θ [pf(τ) -p]为零温时质子 (或中子 )的 Fermi分布函数 (Θ [pf(τ) -p]为阶跃函数 ),RT=t0αρα+1[3-(2x0+1)δ2]/8为核物质的重排项,pFn,pFp分别为中子和质子的 Fermi动量.
图 1给出了 3组参数 (D1,D1S和 D1N)下,不同δ时的每核子能量随密度的变化关系.由图 1可见,对于 3组 Gogny相互作用参数,E(ρ,δ)随同位旋不对称度δ的提高而增加,这说明 E(ρ,δ)是同位旋相关的,当δ=0时,即为对称核物质.研究发现,对任意一组参数,δ=0时的 E(ρ,δ)均在 ρ0=0.16 fm-3左右达到极小值,约为 -16 MeV(即ρ0=0.16 fm-3称为饱和密度),和实验值相符.当δ较大时,E(ρ,δ)在密度很小情况下会出现先增后减再增的现象,甚至当δ大于某个临界值δc后,E(ρ,δ)会随密度单调上升,此时就不存在饱和密度.计算表明,D1参数的δc约为 0.79,D1S的δc约为 0.78,D1N的δc约为 0.83.
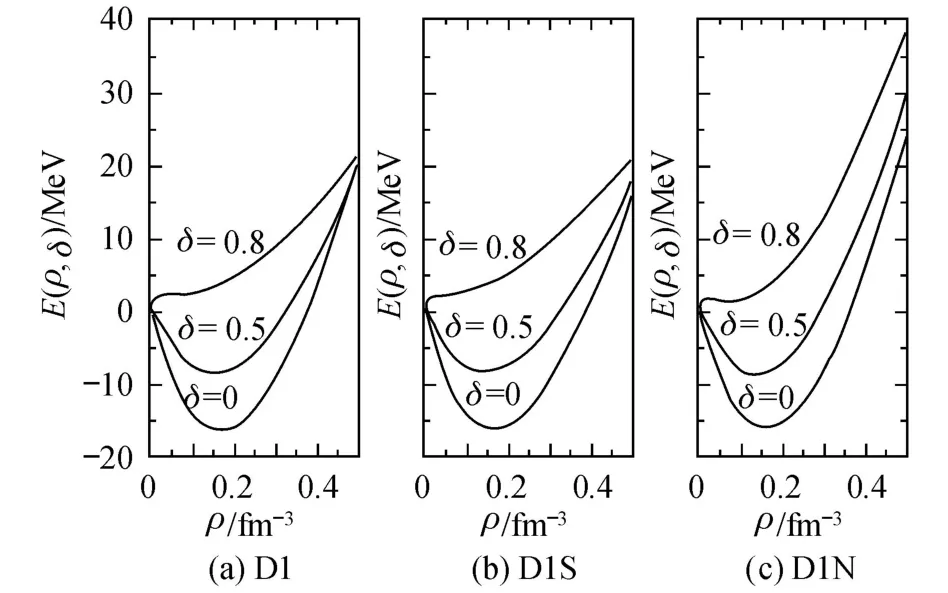
图 1 不同δ下 3组参数每核子能量随密度的变化Fig.1 Relationship between density and energy per nucleon w ith d ifferentδ
在核天文学中,对称能是与中子星中质子的比例、中子星的演化、中子星的半径和密度等密切相关的重要物理量,因此,有关对称能的研究一直是人们十分感兴趣的问题[1].
将每核子能量 E(ρ,δ)泰勒展开[12],其中的就是非对称核物质的对称能Esym(ρ).可以看出,对称能为核子数密度ρ的函数,与δ无关.图 2给出了 3组参数的对称能随密度的变化关系.可以看出,3组参数的对称能随密度都呈先增后减的趋势.在ρ0=0.16 fm-3附近,3组参数的对称能和实验值 30 MeV吻合得很好.目前,关于对称能在密度较大区域究竟是增还是减,并不十分清楚.
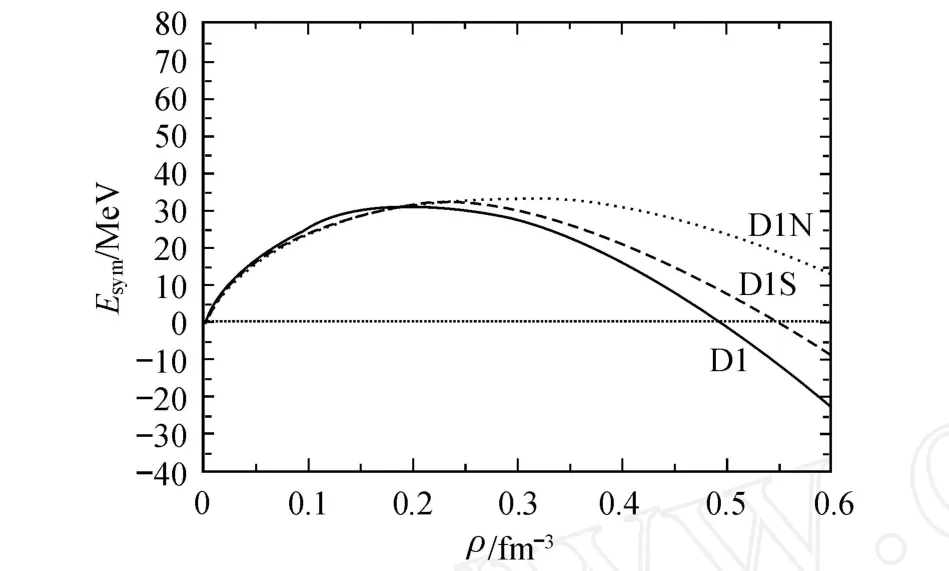
图 2 3组参数下对称能随密度的变化Fig.2 Relationship between density and symmetry energy under three param eter sets of Gogny interaction
2.2 单粒子势(光学势)随核子能量的变化
单粒子势 U(ρ,δ,p,τ)=Uτ表示动量为 p的核子在核子数密度为ρ,同位旋不对称度为δ的核物质中感受到的所有来自其他核子的作用.基于Gogny相互作用的单粒子势可表示为


式中,τ为同位旋第三分量的大小,中子τn=-1/2,质子 τp=-1/2,kfτ=(3π2ρτ)1/3为质子 (或中子 )的Fermi波矢 ,pfτ= ħkfτ为质子 (或中子 )的 Fermi动量.
图 3给出了单粒子势 (光学势[13-15])随单核子能量 E-M的变化关系,其中单核子能量 E-M=可见,3组Gogny参数在能量较大时,单粒子势始终小于 0 MeV,这与实验值 30 MeV不符 (见图 3中 Hama[16]的 Fit 1和 Fit 2).这说明现有的 3组 Gogny相互作用参数还有待改进.
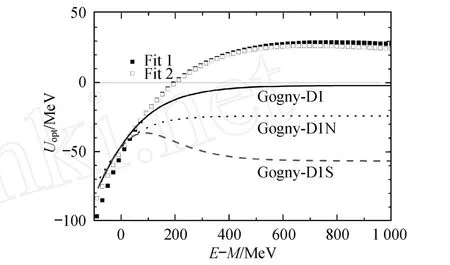
图 3 单粒子势(光学势)随核子能量的变化Fig.3 Relationship between single nucleon energy and single par ticle poten tial(optical poten tial)
2.3 对称势
研究非对称核物质中的对称势,对理解核物理和天体物理中的许多重要物理问题具有重要意义[1].零温时的对称势 Usym定义为
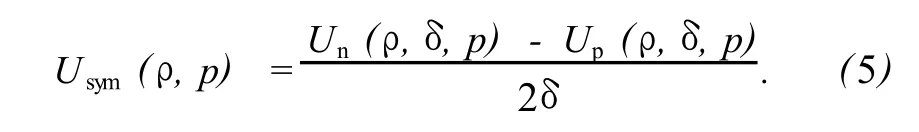
研究表明,Usym(ρ,p)的大小对δ不敏感.为方便起见,取δ=0.5,则对称势简化为

由于中子和质子的质量十分接近,因此,可以看成是质量 m0=939 MeV/c2的核子.图 4给出了对称势随核子动能 Ekin的变化关系.由图可知,D1给出的结果与唯象的动量相关相互作用 (momentumdependent interaction, MD I) 模 型[13-14,17-18]、DBHF(Dirac-Brueckner-Hartree-Fock)理论、非相对论BHF(Brueckner-Hartree-Fock)理论以及相对论冲击近似 (relativistic impulse app roximation,RIA)等微观理论给出的结果类似[15],这与目前公认的结果比较接近:即随着核子动能的增大,中子的单粒子势会逐渐变小,最终会小于质子的单粒子势,使得对称势为负[15].相比较而言,D1S和 D1N这两组参数虽然在核子动能很低的情况下给出的结果与微观理论的结果比较吻合,但当动能继续增大时,特别是动能大于 100 MeV后,对称势将大大偏离实验值.
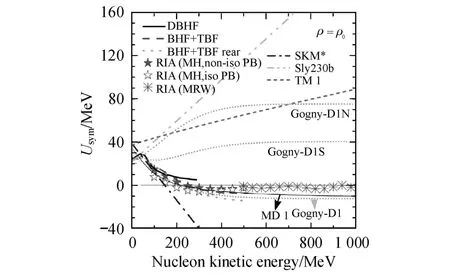
图 4 对称势随核子动能的变化Fig.4 Relationship between nucleon k inetic energy and symmetry potential
2.4 有效质量
在核物理中,另一表征单粒子势性质的物理量为核子的有效质量m*τ.有效质量反应了核子单粒子势的动量相关性[1],其定义式为

在 Gogny相互作用中,非对称核物质中质子和中子的有效质量随动量 p的变化是不同的,这被称为有效质量的同位旋劈裂.
图 5给出了δ=0.5时 3组参数饱和密度时的有效质量随动量的同位旋劈裂.图 6给出了δ=0.5时,在各密度的 Fermi动量处的有效质量随密度的同位旋劈裂.由图 5和图 6可见,D1N给出的最新结果与 D1,D1S区别较大.在图 5中,当动量很大时,3组参数所给出的质子和中子的有效质量都趋于它们的静质量,而最新的D1N参数表现出的中子有效质量始终小于质子的有效质量.在图 6中,D1N给出的结果与 D1,D1S区别更为明显.随密度增大,D1和D1S参数的同位旋劈裂较缓慢.而 D1N参数的同位旋劈裂则随密度的增大变化得很快,并且中子的有效质量几乎总是小于质子的有效质量.但是在丰中子核物质中,已有的研究认为中子的有效质量要比质子大[12],这样看来,D1N的结果不够理想.

图 5 有效质量随动量的同位旋劈裂Fig.5 Isosp in splitting of effectivemass w ith momentum
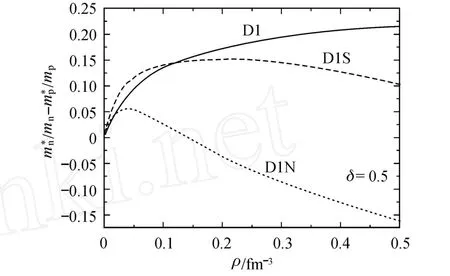
图 6 Ferm i动量处有效质量随密度的同位旋劈裂Fig.6 Isosp in splitting of effectivemass w ith density at Ferm imomentum
2.5 饱和密度处的性质
饱和密度 (每核子能量取极小值时的密度)处的核物质的性质一直是本研究比较关心的问题.这里主要研究不可压缩系数 (等压压缩系数)在饱和密度处的性质.最近的研究表明,δ的高阶项对于确定极其丰中子的中子星外壳内缘分离出液态核时的转变密度起着非常重要的作用[12].

不可压缩系数 K为描述核物质性质的一个重要参量[12],可以用来描述系统的力学稳定性等性质,其定义式为式中 ,为压强.K(ρ,δ)在饱和密度 ρ0处可写为 Ksat(δ),称为等压压缩系数 (isobaric incompressibility)[19].

为了研究等压压缩系数的性质,将对称核物质的每核子能量 E0(ρ)=E(ρ,δ=0)在 ρ0处展开到第四阶,即式中,反映了在具有不对称度δ的非对称核物质中,饱和密度处的不可压缩系数相对于对称核物质 (δ=0)饱和密度处的不可压缩系数的偏移,或者说,反映了等压压缩系数Ksat(δ)对同位旋的依赖性.图 7和图 8分别给出了 3组参数下的等压压缩系数随δ以及δ2的变化关系.

图 7 3组参数等压压缩系数随δ变化Fig.7 Isobar ic incompressib ility vs.δunder three param eter sets
由图 7可见 ,对于 3组 Gogny参数 ,Ksat(δ)随δ的增大总是减小的,最终在临界值δc处,Ksat(δ)仍然大于 0,这说明在饱和密度处,系统总是力学稳定的.由图 8可见,(Ksat-K0)随δ2的变化曲线几乎可以用 Ksat,2δ2这条直线来代替 ,这说明 Ksat(δ)很好地满足了抛物线近似,也说明当斜率参量L比较小时,Ksat(δ)的高阶量对 Ksat(δ)影响不大.
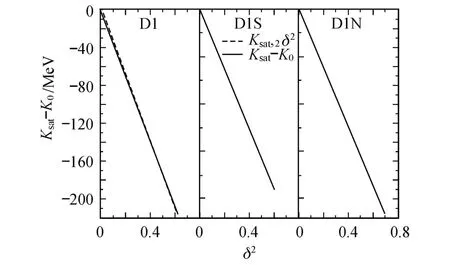
图 8 3组参数的等压压缩系数随δ2的抛物线近似Fig.8 Parabolic approximation betweenδ2and isobar ic incompressibility under three param eter sets
最后,根据计算结果,本研究在表1中给出一些高阶量和关键参数的具体值,其中ρ0为δ=0时的对称核物质的饱和密度,E0/A为对称核物质饱和密度处的每核子能量的值.可以看出,3组参数下的ρ0,E0/A,Esym(ρ0)的值与实验值比较吻合.但是需要指出的是,这 3组参数下斜率参量 L的最大值均不超过 33.6 MeV,这和实验值 L=60.0 MeV相比,还是偏小的.这也说明现有的 3组 Gogny相互作用参数还有待改进.

表1 3组参数下一些高阶量和关键参数Table 1 Values under three sets of Gogny parameter s
3 结 束 语
本工作基于 Gogny相互作用,研究了零温均匀无穷大非对称核物质的同位旋相关性.结果发现,现有的 D1,D1S和 D1N 3组参数都与实验值 (趋于30 MeV)差距比较大,不能很好地描述非对称核物质的单粒子势;同时,D1S和 D1N也不能很好地描述对称势.另外,从研究的有效质量同位旋劈裂的结果来看,D1N参数给出的结果和预期值相差较大.此外,还研究了等压不可压缩系数 Ksat(δ)的同位旋随不对称度δ的变化关系,讨论了 Ksat(δ)的同位旋依赖的抛物线近似.结果发现,Ksat(δ)能很好地满足抛物线近似,这说明 Ksat(δ)的高阶量对于这 3组Gogny相互作用参数的影响不大.本研究还计算了饱和密度处的对称核物质的性质及对称能的高阶特征参数,列出了一些关键值.过小的L值也说明了寻找新的 Gogny相互作用参数的重要性.
从对比各类模型以及实验值的综合结果来看,现有的D1,D1S和D1N这 3组 Gogny相互作用参数还存在不足,所以给出新的更好的 Gogny相互作用参数是十分必要的.
[1] DECHECHARGÉ J,GOGNY D.Hartree-Fock-Bogolyubov calculationswith the D1 effective interaction on spherical nuclei[J].Physical Review C,1980,21(4):1568-1593.
[2] SKYRME T.The effective nuclear potential[J].Nuclear Physics,1959,9(4):615-634.
[3] DAS C B,GUPTA S D,GALE C,et al.Momentum dependence of symmetry potential in asymmetric nuclear matter for transport model calculations[J]. Physical Review C,2003,67(3):034611.
[4] ZHANG Y J, SU R K, SONG H Q, et al.Thermodynamical p roperties and Coulomb instabilities in hot nuclear systems with the Gogny interaction[J].Physical Review C,1996,54(3):1137-1143.
[5] ÁNGELES M,GARCÍA P.Magnetization of a neutron p lasmawith skyrme and Gogny forces in the presence of a strongmagnetic field[J].Physical Review C,2008,77(6):065806.
[6] KUCHAREK H,RING P,SCHUCK P.Pairing properties of nuclear matter at finite temperature[J].Z Phys A:Atomic Nuclei,1989,334:119-124.
[7] 陈融.非对称核物质的状态方程 [D].上海:上海大学,2009.
[8] FELDMEIER H,L INDNER J.Field-dependent coup ling strength for scalar fields[J].Zeitschrift für Physik A Hadrons and Nuclei,1991,341(1):83-88.
[9] DANIELEW ICZ P. Determination of the mean-field momentum-dependence using ellip tic flow[J].Nuclear Physics A,2000,673:375-410.
[10] CHAPPERT F,GIROD M,HILARIRE S.Towards a new Gogny force parameterization: impact of the neutron matter equation of state[J].Physics Letters B,2008,668:420-424.
[11] SONG H Q,ZHENG GD,SU R K.Critical phenomena in nuclear matterwith Gogny interaction[J].J Phys G:Nucl Part Phys,1990,16:1861-1871.
[12] RING P,SCHUCK P.The nuclear many-body p roblem[M].New York:Sp ringer-Verlag,1980:147-177.
[13] LÁSZLÓ P,CSERNA I G F,CHARLES G,et al.Nuclear equation of state with momentum-dependent interactions[J].Physical Review C,1992,46(2):736-747.
[14] CHEN L W,KO C M,L I B A.Determination of the stiffness of the nuclear symmetry energy from isospin diffusion[J].Phys Rev Lett,2005,94:032701.
[15] L IB A,CHEN L W,KO CM.Recentprogress and new challenges in isospin physics with heavy-ion reactions[J].Physics Reports,2008,464:113-281.
[16] COOPER E D,HAMA S,CLARK B C,et al.Global Dirac phenomenology for proton-nucleuselastic scattering[J].Physical Review C,1993,47(1):297-311.
[17] 徐骏.非对称核物质热力学性质、中子星结构和蒙特卡罗算法相关问题的研究[D].上海:上海交通大学,2008.
[18] WELKE G M,PRAKASH M,KUO T T S,et al.Azimuthal distributions in heavy ion collisions and the nuclear equation of state[J]. Physical Review C,1988,38(5):2101-2107.
[19] CHEN L W,CA I B J,KO C M,et al.Higher-order effects on the incompressibility of isospin asymmetric nuclear matter[J].Physical Review C,2009,80(1):014322.
Isosp in Dependent Proper ties of Asymmetr ic Nuclear M atter Using Gogny Interaction
CHEN Rong1,2, YANG Yan-fang1, CHEN Lie-wen2
(1.College of Sciences,ShanghaiUniversity,Shanghai200444,China;2.Department of Physics,Shanghai Jiao Tong University,Shanghai200240,China)
Using the finite-range Gogny interaction,the equation of state(EOS)and the single-particle potential as well as their isosp in dependence in isosp in asymmetric nuclear matter is studied.By comparison with othermodelsand empirical values,we show the limitation of the Gogny interactionsD1,D1S and D1N,and necessity of a new parameterization of Gogny interaction.
Gogny interaction;asymmetric nuclear matters;equation of state(EOS);isospin
O 571
A
1007-2861(2011)02-0164-06
10.3969/j.issn.1007-2861.2011.02.011
2009-09-23
国家自然科学基金资助项目(10575071,10675082);上海市青年科技启明星计划资助项目(06QA 14024),国家重点基础研究发展计划 (973计划)资助项目 (2007CB815004);上海市重点学科建设资助项目(S30105)
杨艳芳 (1973~),女,副教授,博士,研究方向为物理学.E-mail:yangyangzhaoyb@yahoo.com.cn
(编辑:刘志强)
自量子色动力学 (quantum chromodynamics,QCD)被提出以来,人们对强相互作用有了进一步的认识.虽然QCD可以描述强相互作用,理论上也应该可以推导出核力,但是在使用 QCD解决具体问题时,其复杂性令其难以直接求解.而核物理研究的一个极为重要的部分,就是找到真正的“核力”.为此,人们构造了含经验参量的简化模型来处理与核力相关的具体问题,如基于零程的 Skyrme相互作用的Hartree-Fock理论和基于介子交换模型的相对论平均场理论等.
1980年,Gogny等[1]提出了 Gogny相互作用,修正了 Skyrme作用的一些不足之处,并对 Gogny相互作用进行了计算,给出了与实验吻合得更好的结果.因此,本研究使用 Gogny相互作用.
