考虑停车视距的优化速度函数
2011-10-20董力耘李兴莉戴世强
宋 涛, 董力耘, 邝 华, 李兴莉, 戴世强
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.广西师范大学物理科学与技术学院,广西桂林 541004;3.太原科技大学应用科学学院,山西太原 030024)
考虑停车视距的优化速度函数
宋 涛1, 董力耘1, 邝 华2, 李兴莉3, 戴世强1
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.广西师范大学物理科学与技术学院,广西桂林 541004;3.太原科技大学应用科学学院,山西太原 030024)
在分析优化速度函数性质的基础上,提出有理函数型优化速度函数的一般表达式.该函数以曲线拐点对应的临界间距为特征控制参数,并能构造非凹基本图.利用临界间距的重尺度化关系式,采用停车视距构建一种新的优化速度函数,以表征人-车-路环境交互影响下的司机驾驶行为.与其他优化速度函数对比分析后可以发现,新的优化速度函数能够更好地反映与驾驶行为关联的流密关系数据散布、通行能力变化等实际交通特征.
优化速度函数;非凹基本图;临界间距;停车视距;驾驶行为
1995年,del Castillo等[1]提出了由速度-密度(简称速密)关系曲线描述的几类函数形式,并据此给出了构建凹的基本图的方法.但直到目前为止,尚未有关于构建非凹基本图以及同时描述 S形速密和速度-间距 (简称速距)关系曲线的普遍方法.这里“非凹基本图”是指流密关系函数不仅是凹函数形式的基本图,也并非单纯的凸函数.以前研究的基本图通常是凹的,而非凹基本图中存在拐点,使得函数的凹性发生变化.表现在中小密度范围内呈现凹性,大密度范围内呈现凸性.本研究分析了优化速度函数的数学性质,提出以 S形曲线拐点对应的临界间距为关键控制参数的函数形式,依此构建一类优化速度函数簇,并同时获取非凹基本图.将临界间距重尺度化为停车视距后,新的优化速度函数能够反映交通流受到人-车-路交互环境的影响情况.对比分析正常和限速路况下速距和流密关系曲线,并考虑司机的驾驶行为可以发现,新的优化速度函数既能反映经验观测中的流密关系形状,又可描述数据散布、道路通行能力变化等多种交通现象.
1 优化速度函数的数学性质和新的函数表达式
目前,在优化速度类模型中,一般使用 S形曲线的速距关系函数又称优化速度函数 (optimal velocity function,OVF)来构造非凹基本图.针对高速路交通流建模,常见的有两类优化速度函数:一类是 Bando等[5]根据日本高速公路实测交通数据提出的 tanh型函数

另一类则是Mahnke等[9]对比德国高速公路的实测交通数据[8]提出的二阶 Hill型函数

式中,h为车头间距.优化速度函数 Vopt(h)反映了车辆在定常均匀态下,速度与 h之间的单值映射关系.
研究表明[1,7,10-13],优化速度函数必须满足以下数学性质:
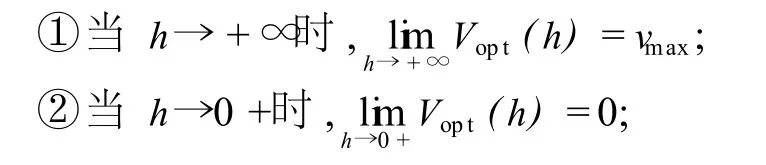
③存在 hstop>lc的某个值,使得 h∈[0,hstop]时,Vopt(h)≡0;
④当 h>hstop时,Vopt(h)>0且有界;
⑤当h>hstop时,V′opt(h)>0,即Vopt(h)是关于h的单调递增函数;
⑥存在 hI>hstop的某个值,使得 hstop<h<hI时,V″opt(h)>0,而h>hI时,V″opt(h)<0.
上述 5点性质中:vmax表示 OVF的上界值,由车辆自身和当前路况同时决定;hstop表示堵塞车头间距,对应于现实的特征堵塞密度ρjam,其值大于车长lc.OVF的单调性和可微性则可表征交通流中连续光滑过渡机制的可能存在性[1].近期,众多研究人员[7,10-12]指出:性质⑥是优化速度函数必备的,即OVF必须是 S形曲线,(hI,Vopt(hI))为其拐点.V′opt(h)在h>hstop时,仅有一个最大值V′opt(hI),这样就可根据模型的稳定性判据,划分“稳定→不稳定→稳定”三个连续的交通区域,从而能够自发地产生稳定的时停时走波或扭结反扭结波.对于 S形的OVF,其关键参数 hI通常认为是车辆之间是否产生相互作用的特征距离,这也意味着在车头间距处于hI附近时,司机驾车很难维持稳定车速 Vopt(hI),从而产生不稳定性.因此,本研究中称 hI为临界间距(critical headway).目前,OVF中的临界间距是通过数据拟合的手段来确定的[5,9],且仅在 tanh型优化速度函数中显式表达,即式 (1)中的“25”.
经过研究发现[13],可以通过有理函数显式表达临界间距作为控制参数,这样便可据此构建新的OVF表达式,并预期获得非凹基本图.不妨令 h^-1=(h-hstop)/hstop,即选取特征长度 hstop无量纲化 h.不失一般性,期望的优化速度函数可记为

式中,n>1且为整数.为了便于分析,有以下假设:

(3)令 aj=bj=0,j=1,2,…,n-1,且记 D:=b0/bn(b0,bn>0),则 VRopt满足 OVF的数学性质④,⑤和⑥.

另外,由式 (6)可知,vmax,hstop和 hI为量纲控制参数,其中 vmax和 hstop一般被视为交通流的特征参数,可取定值[1],而 hI的取值可由数据拟合的方法确定[5].本研究则给出另一种解决方案,即采用一种特征距离重尺度化的方法确定临界间距 hI的数值.
2 临界间距的重尺度化和停车视距
临界间距可视为车辆从相互作用转变为非相互作用的一种特殊的“距离长度”[5,7,9].由于车辆的行驶受到司机以及道路环境的影响,临界间距是人-车-路环境下司机驾车行为的一种表征,与司机的驾车特性和习惯密切相关.
众所周知,司机通常会保持一个安全行车距离.以当前车速行驶的车辆在到达前方的“固定物体”之前安全停车的距离称为停车视距[2-3](stopp ing sight distance,SSD).SSD由感觉-反应距离 dr:=v0τ和制动距离组成,其中τ为司机的感觉-反应时间(percep tion-response time,PRT),v0为司机在感觉接受信息时的车速,G为车辆的自身重量,Gb为配备制动器闸的轮轴所能支撑的重量,g为重力加速度,μ为车辆轮胎与道路表面的摩擦系数.可以看出,停车视距依赖于车速、司机驾驶行为以及道路和车辆自身性能的特征长度.
这里需特别指出的是,PRT作为交通流理论中描述司机行为的一项关键参数,之前一直是作为常值被引入微观交通流建模的[2-3,5,7].但近期的研究发现[3,14],PRT事实上是一个时变量,不存在用一个所谓较好的常值来代替.针对各类行车事件以及司机的生理和个性差异,PRT的取值是变化的,统计后的典型值也各不相同,例如高预期性事件的 PRT为0.70~0.75 s,意外物体和突发事件出现时的 PRT分别为 1.57和 2.45 s,最大的正常的 PRT也会高达6 s.因此,正常的 PRT取值范围[3]为τ∈[0.5,6],故此也有关于采用随机变量形式 PRT的交通流建模研究[15].
另外,制动距离 db中的一个重要控制参数为摩擦系数μ,它主要受车轮的结构和材料以及道路表面形状与材质影响,天气条件变化对其的影响也很大.一般建议的取值为干燥水平道路μ=0.65,潮湿水平道路μ=0.35[2-3].
工程上为了保证安全性,取 v0=vmax和G=Gb来计算 SSD[2-3],因此 ,有
式 (8)满足人们考虑发生的“最坏可能情况”.
通过对一系列优化速度函数进行比较分析可知[13],临界间距一般为堵塞车头间距的 2~5倍,即13~50 m量级,这与实际交通流情形吻合.但是,直接将式 (8)作为临界间距的计算公式引入式 (6)是不合适的,因此,需要先将 SSD重尺度化.
假设停车视距和临界间距的重尺度化关系为
式中,m>0且为有理数.考虑上述 hI与 hstop的倍数关系,可用不等式

表征停车视距与特征参数 hstop之间的尺度联系.用重尺度化的 SSD代替式 (6)中的临界间距,从而得到一类可表征驾驶行为的优化速度函数.
3 考虑停车视距的优化速度函数
由于引入了停车视距作为重尺度化的临界间距的表征,可以在一定程度上表示司机在人-车-路环境交互作用下的一种驾驶行为.我们将这种表征驾驶行为(driving behavior,DB)的优化速度函数称为DBOVF,其具体表达式为

式中,停车视距的计算公式见式 (8).考虑到有三次可微性质的 OVF具有持续研究的可能性[7,11-12],我们选择 n=3,根据式 (10),可确定 m=1.8.其他参数建议取值[1]分别为m.下文就 PRT是统计平均意义上的固定值情况进行分析,取正常行驶条件下司机的感觉-反应时间τ=1.5 s[2-3,12,14],μ为 0.65和 0.35分别对应普通和低摩擦路况情形.对限速情况的 OVF和 FD也进行了详细的对比讨论,而对 PRT为时变量的情况以及与OVF相关的动力学模拟研究,则另文专述[13].
图 1综合显示了正常和限速条件下以及经过参数标定的优化速度函数的比较结果.我们分别就优化速度函数和基本图进行对比分析,其中正常路况下 vmax值取 33 m/s,限速条件下 vLmax值取25 m/s.从图1(a)可以看出,DBOVF在普通路面上的表现和Bando OVF接近一致,特别是在 20~30 m处曲线重合,在 48 m处达到 vmax值的 95%,在稍大于41 m处分别达到 vmax值 95%的 Bando和 Mahnke OVF.另外,在低摩擦力路面上,由于考虑驾驶安全,DBOVF的取值整体上低于正常路面行车速度,这和我们预期的一致.图 1(b)则给出了关于流量的宏观量级比较,显然,DBFD也能正确预测道路的实际通行能力,在密度为 30 veh/km时流量达到最大值 2 632 veh/h,略低于 Bando基本图预测的在 29 veh/km处达到最大值 2 785 veh/h.而Mahnke基本图由于标定时仅和畅行交通的数据一致,没有拥挤交通数据的验证,因而无法合理预测拥挤交通范围内的速度和流量.整体而言,对于普通高速路的流密关系,三类基本图的表现在自由流区域一致,而低摩擦力路面的DB基本图整体小于正常路面的现象也符合常理.在正常路面条件下,Bando和 DB基本图均显示流量在各自的ρjam密度的 20%处达到最大,而低摩擦力路面的临界密度小于此值主要是由于安全驾驶导致的制动距离增大的缘故.
文献[5]建议在限速情况下采用小参数修正OVF的方法,即图 1(c)和 1(d)中的Bando与Mahnke的优化速度函数就是这样描述的,而 DBOVF则直接使用了 vLmax替代原有的 vmax,不过需注意 SSD中的 vmax也要同时被替换.为了合理反映司机的 PRT变化,取 0.7,1.5,2.5 s依次表征司机在高预期性事件、突发事件以及安全行驶下的PRT值.另外,为了反映由于天气变化的影响而引起的限速,我们也考虑了潮湿和干燥路面摩擦系数的变化.图 1(c)显示了一系列速度变化的结果,可以看出,司机在紧张的高预期心理活动下,速度值均偏高,反映了小尺度的PRT具有促使司机加快行程的作用.而基于安全因素的考虑,司机在潮湿路面上驾车时会小心翼翼,速度值偏低,反映了司机针对天气变化对路面的影响和车辆制动考虑下安全驾驶的行为.

图 1 正常路况和限速条件下优化速度函数以及基本图的对比Fig.1 Compar ison of optimal veloc ity functionsand fundam ental d iagram s under normal and speed lim it road cond itions
图 1(d)刻画了限速条件下基本图的变化.基本图反映了直接用小参数修正原有 OVF可能存在过多折减通行能力的弊端.一般而言,限速会增大司机的 PRT,这是由于驾驶员需要更多时间判断限速区的路况[3].限速区的临界密度会增大,这也是由于司机谨慎驾驶造成的,DBOVF能很好地预测该现象.即使不考虑道路摩擦系数的变化,我们也可以看出,在限速时考虑不同 PRT值的 DBFD涵盖了密度为 20~100 veh/km的二维区域,这与实测的流密关系在中高密度值范围的数据散布现象一致,说明仅考虑司机的驾驶行为也可以导致流密数据散布的结果,补充了现有基本图仅为单值曲线,不考虑人类行为的唯一平衡态的认识.事实上,Bando FD曲线的大部分区域也是落在DBFD的范围之内的.此外,我们也可看到,PRT值的降低即司机的反应速度加快,可以增大临界密度值从而提高道路流量,这是符合经验观测结果的.
需要特别指出的是,优化速度函数式 (11)的指数集 (n,m)并非仅有 (3,1.8)一个选择.在考虑仍然使用停车视距重尺度化临界间距的情况下,指数集 (n,m)选择为 (2,1.2)也可以得到很好的结果[13].如要考虑利用现有标定的临界间距数值,例如 Bando OVF中的 25 m,则使用式 (6),选择 n=5和 hI=25 m同样有令人满意的结果[13].因此,完全可以利用式(6)构建一类优化速度函数簇在实际情况中使用.例如,对于现今使用高摩擦系数路面-彩色防滑路面作为新型交通管理方式的交通流建模,采用考虑停车视距优化速度函数的微观模型已预测出其他模型不能正确模拟的交通波速降低和堵塞消散现象[16].
4 结 束 语
本研究通过分析优化速度函数的数学性质,从有理多项式函数出发构造了一类以临界间距为关键参数的优化速度函数,并给出了一般函数表达式.据此,提出了以临界间距为特征参数构建优化速度函数且获取非凹基本图的方法.随后利用重尺度化的方法,将临界间距表述为停车视距的概念,以表征司机在人-车-路环境交互影响下的驾驶行为.考虑停车视距的优化速度函数在与经典的优化速度函数的比较中显示了一定的优越性,并且一系列图谱刻画了因司机心理活动不同而产生的对优化速度和基本图的影响,弥补了以往单值平衡态基本图因不考虑人的因素而无法准确预测流密关系数据散布的缺陷,加深了人们对交通流的认识.
致谢:感谢孟剑平博士对本研究工作给予的研究建议和积极讨论.
[1] DEL CASTILLO J M,BEN íTEZ F G.On the functional form of the speed-density relationship—(Ⅰ):general theory [J]. Transportation Research Part B:Methodological,1995,29(5):373-389.
[2] LEUTZBACH W.Introduction to the theory of traffic flow[M].Berlin:Springer,1988.
[3] GARTNER N H,MESSER C J,RATHI A.Revised monograph on traffic flow theory[M].Washington D C:Federal Highway Administration,1999.
[4] KERNER B S,KONHÄUSER P.Structure and parameters of clusters in traffic flow[J].Physical Review E,1994,50(1):54-83.
[5] BANDO M,HASEBE K,NAKANISHI K, et al.Phenomenological study of dynamicalmodelof traffic flow[J].Journal de Physique I France,1995,5(11):1389-1399.
[6] L I T.Nonlinear dynamics of traffic jams[J].Physica D,2005,207(1/2):41-51.
[7] W ILSON R E.Mechanisms for spatio-temporal pattern formation in highway traffic models[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,2008,366:2017-2032.
[8] KERNER B S,REHBORN H.Experimental properties of complexity in traffic flow [J]. Physical Review E,1996,53(5):R4275-R4278.
[9] MAHNKE R,KAUPUZS J.Stochastic theory of freeway traffic[J].Physical Review E,1999,59(1):117-125.
[10] NAGATANI T.The physics of traffic jams[J].Reports on Progress in Physics,2002,65(9):1331-1386.
[11] GASSER I,SIRITO G,WERNER B.Bifurcation analysis of a classof‘car following’traffic models[J].Physica D,2004,197(3/4):222-241.
[12] OROSZ G,W ILSON R E,KRAUSKOPF B.Global bifurcation investigation of an optimal velocity traffic modelwith driver reaction time[J].Physical Review E,2004,70(2):026207.
[13] 宋涛.非对称多运动相交通流的建模和模拟 [D].上海:上海大学,2011.
[14] GREEN M. “How long does it take to stop?”methodological analysis of driver perception-brake times[J].Transportation Human Factors,2000,2(3):195-216.
[15] MENG J P,SONG T,DONG L Y,et al.Stochastic carfollowing model for explaining nonlinear traffic phenomena[C]∥The Eighth International Conference on Traffic and Granular Flow.2009.
[16] SONG T,WEI Y F,DONG L Y,et al.Optimal velocity model based on stopping sight sistance:a case study of modeling color antiskid pavement[C]∥The Eighth International Conference on Traffic and Granular Flow.2009.
Optimal Velocity Function Consider ing Stopp ing Sight D istance
SONG Tao1, DONGLi-yun1, KUANGHua2, L IXing-li3, DA IShi-qiang1
(1.Shanghai Institute of Applied Mathematics and Mechanics,ShanghaiUniversity,Shanghai200072,China;2.College of Physics and Technology,GuangxiNormal University,Guilin 541004,Guangxi,China;3.School of App lied Science,Taiyuan University of Science and Technology,Taiyuan 030024,Shanxi,China)
Thispaper dealsw ith the op timal velocity function for traffic flow,characterized by a rational function form.The critical headway is taken as the control parameter and used to establish the nonconcave fundamental diagram.A new optimal velocity function considering stopping sight distance is proposed to describe human driving behavior in the driver-vehicle-road environment by rescaling the critical headway.Compared with other classical optimal velocity functions and related fundamental diagrams,the new function has advantages in explaining real traffic features such as scattering densitydependent flow data and variable highway capacity.
optimal velocity function;non-concave fundamental diagram;critical headway;stopping sight distance;driving behavior
O 29
A
1007-2861(2011)02-0147-06
10.3969/j.issn.1007-2861.2011.02.008
2010-10-19
国家重点基础研究发展计划 (973计划)资助项目 (2006CB705500);国家自然科学基金资助项目 (10532060,10962002,10902076,10972135);山西省自然科学基金资助项目(2010011004);上海大学研究生创新基金资助项目(SHUCX080161)
董力耘 (1971~),男,副教授,博士,研究方向为交通流理论.E-mail:dly@shu.edu.cn
(编辑:孟庆勋)
流量-密度 (简称流密)关系曲线又称基本图(fundamental diagram,FD),其形状和性质一直是交通流理论研究中的基本问题.传统研究[1-3]认为,流密关系函数应是凹的,即流量函数 Q″(ρ)≤0.但 20世纪 90年代中期,Kerner等[4]和 Bando等[5]分别通过对宏观连续介质模型以及微观优化速度模型的研究,认为基本图的凹性变化是振荡波形解产生的充要条件[6-7].近期的交通实测同样证实了基本图可能存在凹性变化的性质[5,7-8].
