圆柱壳体振动陀螺谐振子的品质因数研究*
2011-10-20栾清磊吴宇列
栾清磊,吴宇列*,陶 溢,2,席 翔
(1.国防科学技术大学机电工程及自动化学院,长沙 410073;2.武汉军械士官学校,武汉 430075)
圆柱壳体振动陀螺是一种基于哥氏力原理的固体波动陀螺,其具有能耗小、成本低、可靠性高和寿命长等优点,因而具有很好的发展潜力[1]。
目前在圆柱壳体振动陀螺的研究方面,美国的Watson公司、Innalabs公司等研究机构处于领先地位。其中Watson公司研制的PRO-132-3A型陀螺已经实现器件级的真空封装[2],在全工作温度范围内零偏稳定性小于72°/h,但缺点是Q值较低。Innalabs公司则开发了一款高性能的金属圆柱壳体振动陀螺样品,其精度达到了较高的水平[3]。圆柱壳体振动陀螺由于具有一系列的优点,已经在一些军用和民用场合逐渐得到应用,其发展及应用前景非常广阔[4]。但是目前中高精度的圆柱壳体振动陀螺还不是很成熟,还存在零偏温度稳定性、刻度因子非线性等问题,需要进一步研究。
品质因数是衡量陀螺性能的关键参数,它决定了陀螺的检测灵敏度以及响应速度[5]。品质因数的大小由谐振子的能量损耗机制决定。目前,国内外学者对于圆柱壳体振动陀螺的研究主要是针对陀螺的制造工艺以及处理电路等方面,而对于陀螺的品质因数,尤其是对于陀螺谐振子品质因数的影响因素方面,所做的理论和实验研究都比较少,因而有必要对其进行进一步的研究。
本文首先从理论上对影响圆柱壳体振动陀螺谐振子品质因数的主要因素进行详细的分析,并针对各种影响因素进行实验测试,最后对实验结果进行分析总结。
1 工作原理
图1所示是典型的圆柱壳体振动陀螺结构。这种陀螺是由薄壁圆筒形的谐振环、8个压电电极以及安装支座构成。其中谐振环是产生陀螺效应的部分。8片压电电极均匀分布在底部平面上,用于激励和检测谐振子的振动。底面均匀分布有八个圆孔[6],主要是为保证压电电极能够互不干扰地检测谐振子在工作模态下的振动。
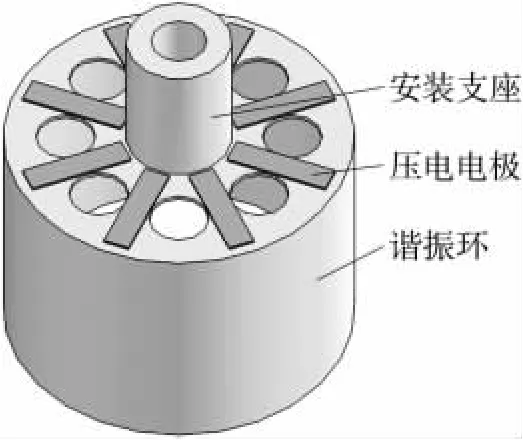
图1 圆柱壳体振动陀螺结构

图2 圆柱壳体振动陀螺工作原理图
圆柱壳体振动陀螺的工作原理如下:给X向分布的一对压电电极施加与谐振子谐振频率相同的交变电压,由于逆压电效应,谐振子的驱动模态被激发,振型为谐振环在X向和Y向上的第一模态振动。当有角速度输入时,谐振环在哥氏力Fc的作用下,在与第一模态呈45°的方向产生第二模态振型,即检测模态,其幅值与角速度大小成正比关系。第二模态的振动传递到X'向和Y'向的四片检测电极,由压电效应产生的信号经过电路和软件处理即可得到输入角速度。
2 理论分析
品质因数是衡量陀螺性能的一个重要指标,它与能量的衰减程度有关[7]。从能量的角度来看,品质因数是系统中存储的总能量与每一个振荡周期中损失能量的比值[8]。每一循环中损失的能量越低,品质因数就越高。因而对于陀螺来说,谐振子的品质因数越高越好。
圆柱壳体振动陀螺工作时其谐振子的能量耗散情况决定了其品质因数的大小。由品质因数的定义以及其物理意义,有[7]
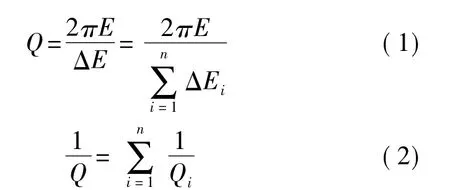
式中E表示振动系统中所存储的总能量,ΔEi和Qi分别表示在一个振荡周期中,第i种能量损耗方式所带来的能量损耗和限制的品质因数。由式(1)可以看出,要得到高的Q值,一方面要保证系统的能量要大,同时还要求能量的损耗尽量小。一般来说,圆柱壳体振动陀螺谐振子在振动时的主要能量耗散形式包括:热弹性损耗、表面损耗以及空气阻尼带来的损耗[9],这三种能量损耗形式所限制的品质因数分别用Qte、Qsurf、Qgas表示,则由式(2)有谐振子的Q值为

谐振子在振动时,会因为其自身内部的热量流动,引起机械能量损耗[10]。由陀螺工作原理可知,谐振子在振动时各部分会交替处于压缩状态和拉伸状态,引起应力的变化并导致温度的改变:压缩状态导致温度升高,而拉伸状态则导致温度降低,这样就产生了热量流动,将机械能转换为不可恢复的热能。谐振子的热弹性能量损耗程度和其材料性质、形状、尺寸和工作温度有关。目前,有关圆筒形状的热弹性损耗方面的理论研究还比较欠缺,主要是通过实验的方法进行研究。
表面能量损耗主要是由表面应力引起的[11],谐振子的机械加工表面质量是影响其表面能量损耗的主要因素。谐振子在经过机械加工后,会造成已加工表面上几微米至几百微米的表面层产生物理机械性能的变化,包括因塑性变形引起的加工硬化、表面层的金相组织变化及表面残余应力等。在谐振子振动过程中,类似于热弹性损耗,表面层也会由于应力变化而引起温度的改变,进而导致能量的损耗。对于圆柱体而言,其表面能量损耗所限制的品质因数Qsurf有[12]

式中h为表面层厚度,T为温度,L和D分别表示圆柱体的高度和直径,E、α、c、ω分别表示材料的弹性模量、热膨胀系数、比热容以及谐振子的谐振角频率,k为与材料有关的常数。由式(4)可知,谐振子的表面能量损耗主要受其材料、尺寸以及加工表面质量的影响。
谐振子在振动过程中,由于空气阻尼的作用,会引起能量的耗散,其能量损耗情况,随着真空度的不同而不同。真空度越高,其能量损耗越小[13],因而为保证陀螺的品质因数,可以对其进行真空封装。
振动系统的品质因数反映了其能量损耗情况,对于圆柱壳体振动陀螺谐振子来说,其材料、尺寸与形状等因素都会影响到其能量耗散情况,因而这些因素均会对谐振子的品质因数产生影响,后面将针对这些影响因素进行实验研究。
3 实验研究
通过前面的理论分析,圆柱壳体振动陀螺谐振子的材料性质、形状以及尺寸等因素都会影响到其品质因数。这里将对相关影响因素进行实验研究,包括谐振子材料、形状及各个尺寸参数对谐振子Q值的影响,另外还对组合形式的谐振子进行了Q值分析。
3.1 谐振子材料对Q值影响
研究谐振子材料对Q值的影响。主要针对锡青铜材料和不锈钢材料进行实验分析,锡青铜相比不锈钢具有更高的机械品质因数。分别采用锡青铜材料和不锈钢材料加工出相同形状尺寸的圆柱壳体振动陀螺谐振子。对这两个谐振子分别进行测试,测试结果如图3所示。

图3 频谱分析图
图3(a)、图3(b)分别是锡青铜谐振子和不锈钢谐振子的频率响应曲线。由测试结果得出锡青铜谐振子的Q值为10 000,不锈钢谐振子的Q值为6300。这主要是由于锡青铜材料的机械品质因数要高于不锈钢材,由此说明材料的机械品质因数越高,加工而成的谐振子Q值也越高。
3.2 谐振环形状对Q值影响
将谐振子的谐振环部分分别做成等壁厚和有阶梯壁厚的圆筒结构,分析谐振环形状对于谐振子Q值的影响。如图4所示,相比等壁厚的谐振子,阶梯壁厚谐振子的谐振环与底部驱动部分之间有一段壁厚相对较薄的圆环,主要起到导振的作用。除了存在导振环结构的区别,等壁厚谐振子的其它尺寸与阶梯壁厚谐振子的完全一致。

图4 不同形状的谐振环
阶梯壁厚谐振子的频率响应曲线如图3(b)所示,Q值为6 300。图5所示为等壁厚谐振子的频率响应曲线,得出其Q值为2 800。相比阶梯壁厚的谐振子,等壁厚谐振子的品质因数有明显的降低,增益也有一定程度的减小。这是由于等壁厚谐振子缺少导振环,导致受到的约束力相对要大很多,从而限制了其振动性能,致使其Q值受到了影响。

图5 频谱分析图
3.3 谐振子尺寸对Q值影响

图6 谐振子主要尺寸参数
主要对等壁厚的谐振子进行分析,如图6所示为陀螺谐振子的主要尺寸参数。初取参数谐振环外径D=25 mm,壁厚a=1 mm,高度h=20 mm,底部厚度b=0.3 mm。当分析某特定参数对Q值的影响时,保持其他参数不变,改变待分析的参数数值进行实验研究。
研究谐振环外径对谐振子Q值的影响。对不同外径D的谐振子进行测试,得到结果如表1(f为谐振频率)所示。
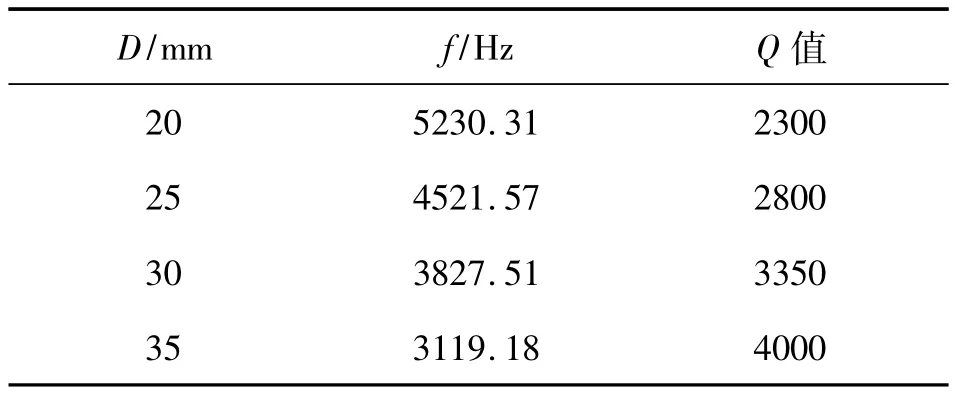
表1 谐振环外径对Q值的影响
研究谐振环高度对谐振子Q值的影响。对不同高度h的谐振子进行测试,得到结果如表2所示。

表2 谐振环高度对Q值的影响
研究谐振环厚度对谐振子Q值的影响。对不同厚度a的谐振子进行测试,得到结果如表3所示。

表3 谐振环厚度对Q值的影响
研究底部厚度对谐振子Q值的影响。对不同底部厚度b的谐振子进行测试,得到结果如表4所示。
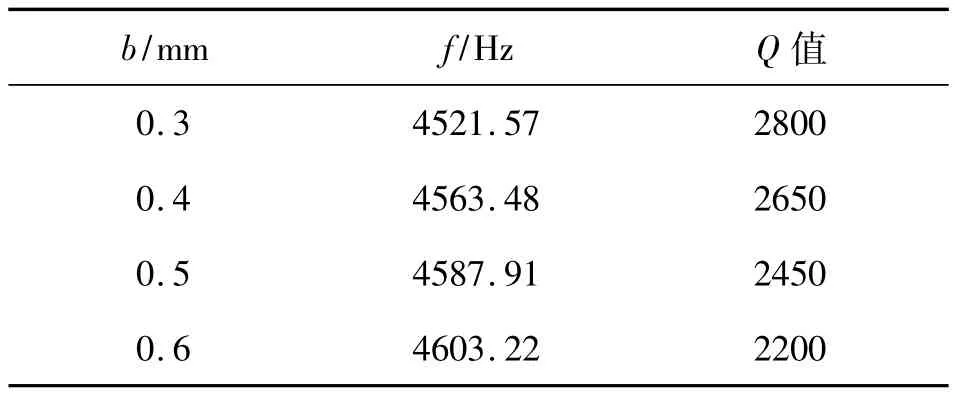
表4 谐振子底部厚度对Q值的影响
通过观察表1~表4的数据可知,谐振子的Q值随着谐振环外径D和高度h的增大而增大,随着谐振环厚度和底部厚度的增大而减小。其中谐振环外径对于谐振子的Q值影响最大。
3.4 组合式谐振子结构对Q值影响
为降低加工难度,谐振子可以采用组合式结构,如图7所示,即将圆柱壳体振动陀螺的谐振子分成上下两部分分别进行加工,上部分是谐振部分,下部分是驱动部分,然后再采用胶接的方法把这两部分牢固的联接成一体。
相比整体加工的谐振子,组合式谐振子由于联接胶的阻尼作用在一定程度上会降低其Q值。

图7 组合式谐振子
图8是组合式谐振子的频率响应曲线。由测试结果得出组合式谐振子的Q值为5900。由图3(b)知整体加工谐振子的Q值为6300,所以组合式谐振子的品质因数相比整体加工谐振子的减小幅度不大。这是由于胶接部分位于导振结构的底部,而影响谐振子品质因数的关键部分在谐振环上,因而联接胶的阻尼作用对谐振子的整体影响不大,从而保证了谐振子的品质因数。

图8 频谱分析图
4 结论
本文通过对圆柱壳体振动陀螺谐振子品质因数的影响因素进行理论分析,并针对相关影响因素进行了一系列实验研究,包括谐振子的材料、形状以及尺寸等因素对于谐振子品质因数的影响,得到如下结论:
(1)谐振子材料本身的机械品质因数在很大程度上决定了谐振子的Q值。材料的机械品质因数越高,加工而成的谐振子Q值就越高。因而选择高机械品质因数的谐振子材料,是获得高Q值谐振子的关键所在。
(2)谐振环的形状也是谐振子Q值的主要影响因素。在谐振部分和驱动部分之间通过导振环结构连接,能够减小谐振环所受到的约束力,进而使得陀螺谐振子的Q值得到提高。
(3)在谐振子的各个尺寸参数中,谐振环外径对谐振子Q值的影响最大,且外径越大谐振子的Q值越高。谐振子的其它尺寸参数也对其Q值产生一定的影响。整体来说,谐振子Q值随着谐振环高度的增大而增大,随着谐振环厚度和底部厚度的增大而减小。
(4)组合式谐振子的品质因数,相比整体加工的谐振子减小幅度不大,说明影响谐振子Q值的最主要因素是在谐振环上。这种结构形式这也为圆柱壳体振动陀螺的研究提供了一个新的思路。
[1]Chikovani V,Yatzenko Y.Coriolis Force Gyroscope with High Sensitivity[P].United States Patent 7281425B2,2008.
[2]William S Watson.Vibratory Gyro Skewed Pick-off And Driver Geometry[J].Journal of Micro Machines,2010,4(10):171-179.
[3]Chikovani V,Okon I,Barabashov A,et al.A Set of High Accuracy Low Cost Metallic Resonator CVG[C]//Proceedings of the IEEE/ION Position,Location And Navigation Symposium,2008:238-243.
[4]吴校生,卢奕鹏,陈文元.压电型微固体模态陀螺的模态及谐振分析[J].传感技术学报,2008,21(12):2014-2019.
[5]Blom F R,Bouwstra S,Elwenspoek M,et al.Dependence of the Quality Factor of Micromachined Silicon Beam Resonators on Pressure and Geometry[J].J Vac Sci.and Tech.B,1992,10(1):19-26.
[6]Chikovani V V,Yatsenko Y A,Barabashov A S.Improved Accuracy Metallic Resonator CVG[C]//A&E SYSTEMS,2009,5:40-43.
[7]Thomas L Floyd.Electric Circuits Fundamentals[M].Prentice hall,2009.
[8]张灵霖,车录锋,李玉芳,等.基于阶跃响应的加速度计Q值测试方法研究[J].传感技术学报,2009,22(10):1417-1421.
[9]Hosaka H,Itao K,Kuroda S.Damping Characteristics of Beam-Shaped Microoscillators[J].Sensors and Actuators:A,1995,49:87-95.
[10]Tudor M J,Andres M V,Foulds K W H,et al.Silicon Resonator Sensors:Interrogation Techniques and Characteristics[J].IEEE Proceeding,1988,135(5):364-368.
[11]Grossmann A,Erley W,Hannon J B,et al.Giant Surface Stress in Hetero Epitaxial Films:Invalidation of a Classical Rule in Epitaxy[J].Phys.Rev.Lett.,1966,77:127-130.
[12]Uchiyama T,Tomaru T,Tobar M E,et al.Mechanical Quality Factor of a Cryogenic Sapphire Test Mass for Gravitational Wave Detectors[J].Physics Letters A 261,1999:5-11.
[13]CHE L F,LU Y,XU ZH N.Finite Element Simulation on Packaging of Hinged High-gMicromachined Accelerometer[J].Opt.Precision Eng.,2007,15(2):199-205.
