半电极含金属芯压电纤维的动态微力传感器*

边义祥，裘进浩

(1.扬州大学 机械工程学院，江苏 扬州 225127;2.南京航空航天大学机械结构强度与振动国家重点实验室，南京 210016)

压电材料同时具有传感和驱动性能，可以用作传感器或驱动器。为了适应特殊的应用需要，很多学者正在研究特殊形状的压电器件，如压电陶瓷纤维、薄膜、薄壳等［1］。裘进浩等［2］和 Hiroshi Sato等［3］先后研制成功的含金属芯压电陶瓷纤维MPF(Metal-Core Piezoelectric Ceramic Fibers)，就是一种新型的压电器件。当MPF只有一半的纵向表面喷镀金属层时，称为半电极含金属芯压电纤维HMPF(Half Coated Metal Core Piezoelectric Fiber)。

自从MPF和HMPF研制成功后，一些学者对MPF进行了理论和实验研究。Gael Sebald等建立了MPF的物理振动模型，分析了MPF的性能及金属芯的影响［1，4］，研究了 MPF 的机电特性［5］;Hiroshi Sato等测量了 MPF的机械性能［6］，把 MPF粘贴在梁的表面，利用MPF的传感和驱动性能制作了智能复合材料悬臂梁［3］;Kiyoshi Takagi等在碳纤维复合材料中埋入MPF，实现了振动控制和结构损伤监测［7，8］;Davood Askari等分析了 MFC 和 MPF 的机械性能的异同点［9］。Hiroshi Sato等还从电极配置、机电转换效率、机械性能、所需电场等方面分析了MFC和MPF之间的区别［10］。国内主要有南京航空航天大学展开了MPF的研究工作，刘建、常伟杰等把MPF粘贴在复合材料板的表面，建立了MPF对圆形压电片激励Lamb波的传感响应模型，并应用这个模型对复合材料板的损伤进行定位［11－12］。

上述研究几乎都是关于表面全覆盖电极的MPF，而在很多情况下，例如气流传感、弯曲驱动等方面，HMPF更能发挥重要的作用。本文作者之一的裘进浩在世界上首次成功制作了 HMPF［13］。在以前的工作中，我们研究了HMPF的静态本构关系方程［14］和驱动性能［15］。为了扩展 HMPF的应用范围，有必要研究其传感性能。本文根据第一类压电方程，基于振动理论，使用平均电荷方法，研究了悬臂梁结构的HMPF自由端外加垂直简谐作用力时，电极上产生的电荷值，由此建立了动态微力传感模型;分析了HMPF长度和半径比对产生电荷值的影响，并实验验证了所建立的传感模型。

1 理论建模

1.1 压电方程

HMPF的几何形状和横截面分别如图1和图2所示。由于是圆柱形，为了研究方便，采用圆柱坐标系，压电方程的直角坐标系和圆柱坐标系的对应关系为，直角坐标系的1方向、2方向和3方向分别对应圆柱坐标系的z方向、θ方向和r方向。

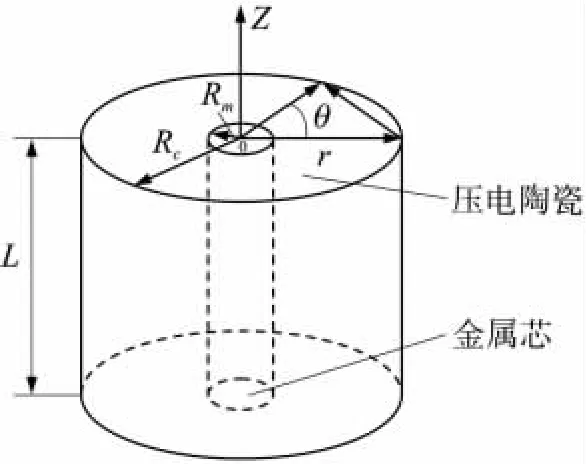
图1 HMPF的几何形状及坐标表示

图2 HMPF的横截面及其极化示意图

如图2所示，HMPF的上半部分压电陶瓷表面覆盖了金属层。外加电压时，压电陶瓷内部的电场分布比较复杂，为了研究方便，认为表面覆盖电极的上半部分压电陶瓷极化后，具有压电效应，其极化方向也认为是径向分布;认为表面没有覆盖电极的下半部分压电陶瓷没有被极化，不具有压电效应。由于陶瓷表面的金属层很薄，在下面的研究中，其影响不予考虑。

当HMPF用作悬臂梁结构时，假设其压电陶瓷部分在径向可以自由伸缩;和长度相比，HMPF的半径很小，其圆周方向和切向的应力可以忽略。外加电场后，其应力和电场的边界条件可以表示为:

所加电场方向和极化方向相反时，压电陶瓷产生伸长变形。根据第一类压电方程，当d31取负值时，其应变和电位移分别为

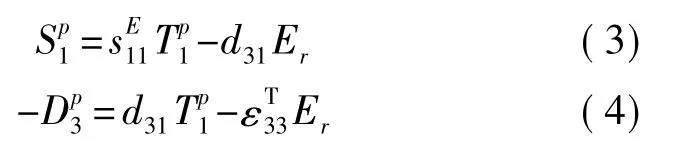
其中的Sij是应变，Tij是应力，Di是电位移，Er是电场强度是弹性柔顺系数，dij是压电常数，是介电常数，上标p表示压电陶瓷极化部分。由于是圆柱形状，在HMPF的电极上外加电压后，半径r处的电场强度为

而下半部分压电陶瓷以及金属芯的应力应变关系为

上标m和n分别表示金属芯和下半部分没有被极化的压电陶瓷。

1.2 HMPF的微力传感模型

悬臂梁结构HMPF的自由端受到动态弯矩M时，由于HMPF的长度和半径比很大，可以认为HMPF各纵向纤维的曲率半径相同，都为ρ，则

其中Mm是金属芯部分所受弯矩，Mc是整个压电陶瓷部分所受弯矩，Em是金属芯的弹性模量，Ec是整个压电陶瓷部分的弹性模量，Im是金属芯的惯矩，Ic是整个压电陶瓷部分的惯矩。联立式(8)和式(9)，并由Em=1/sm和Ec=1/sE11可解得

由1/ρ=M/(EI)，得到整个HMPF的等效的抗弯刚度EI

当动态激励力F=F0ejωt垂直作用在悬臂梁结构HMPF自由端时，HMPF的中性层在极化部分和未极化部分的结合面上，如图3所示。此时，HMPF是均匀等截面直梁，可以得到HMPF的弯曲振动模型［16］

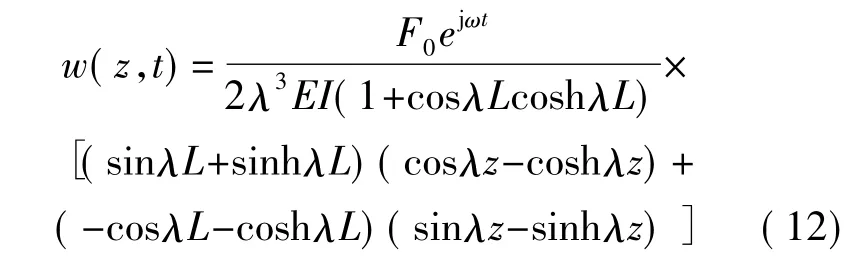
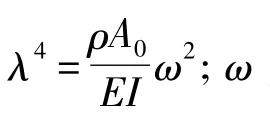
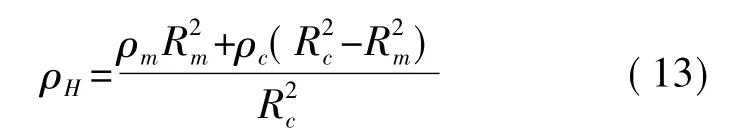
ρc和ρm分别表示压电陶瓷和金属芯的密度。由此，得到HMPF的曲率

则HMPF的应变可以表示为

把式(15)代入式(3)和式(4)中，并由Er=0，得到压电陶瓷极化部分电位移为:

由式(16)得压电陶瓷极化部分外表面和内表面的电位移，即电荷密度分别为:

用平均电荷方法［17］，得到HMPF表面电荷为

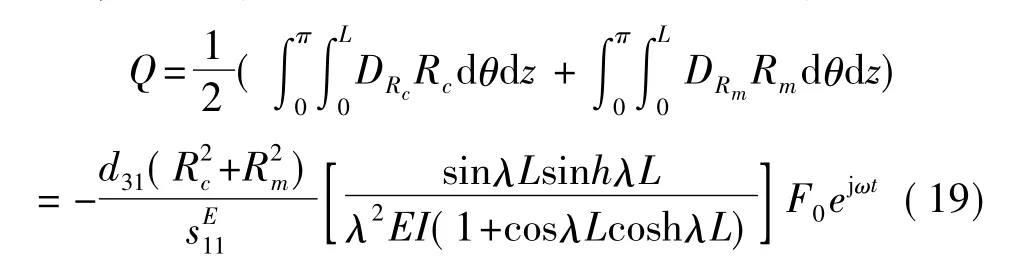
1.3 长度和半径比的影响

由式(19)可知，当悬臂梁结构HMPF自由端受到正弦激励作用时，HMPF产生的电荷也是正弦信号，频率和激励频率相同。如果不考虑时间因素的影响，式(19)可以写成:

进而得到:

当HMPF的参数确定后，测量到HMPF产生的电荷频率和幅值，根据式(19)和式(21)可以算出激励力的频率和幅值。

为了研究HMPF半径比对产生电荷幅值的影响，把半径比B=Rm/Rc代入式(20)，得

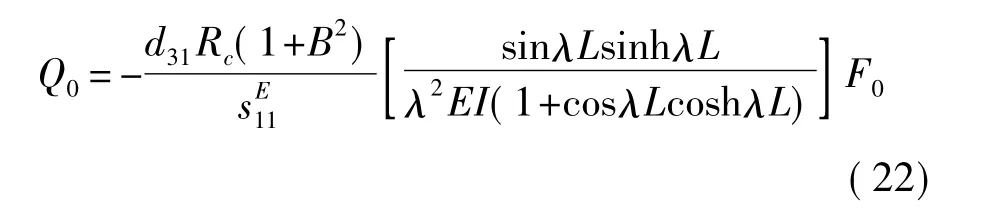
为了研究HMPF结构尺寸对HMPF产生电荷的影响，把HMPF的参数代入到式(22)中进行计算。含铂金芯HMPF的参数见表1。设所加激励力的参数:f=10 Hz、F0=0.000 1 N。逐渐增大 HMPF的长度和半径比，HMPF产生的电荷幅值如图3所示。由图可见，在悬臂梁结构HMPF自由端激励力频率和幅值不变的情况下，HMPF产生的电荷幅值随着长度的增加而增大，在半径比为0.44处取最大值。如果要提高HMPF动态微力传感器的灵敏度，可以采用增加长度和选择合适半径比的方法。

图3 含铂金芯HMPF动态微力传感器电荷幅值和结构尺寸的关系

由以上的分析可知，悬臂梁结构HMPF动态微力传感器参数确定后，根据其电荷的频率，可以测量激励力的频率;根据电荷的频率和幅值，可以测量激励力的幅值。

2 实验研究

为了验证HMPF的动态微力传感性能，搭建如图4所示的实验系统。把一根HMPF一端固定在激振器的激振头上，另一端搭在电子天平上。当激振器低频振动时，HMPF受到电子天平动态微力作用。

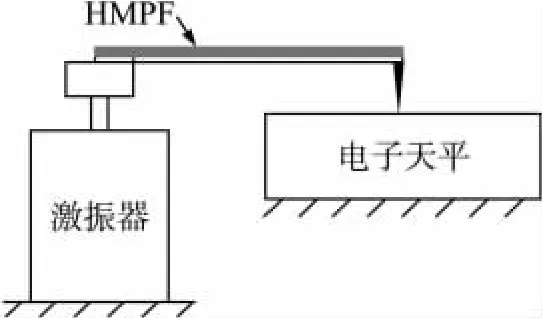
图4 HMPF动态微力传感器实验系统

电子天平的读数和HMPF产生的电荷信号经过电荷放大器、dSPACE卡输入到计算机中。HMPF长度为36 mm，其它参数如表1所示。

表1 MPF的材料性能

HMPF产生电荷的时域信号，经过FFT变换为频域信号后，可以得到HMPF产生电荷的频率。取时域信号中电荷幅值的平均值，由式(21)可以得到激励力的幅值。一组动态微力幅值的测量结果如图5所示。

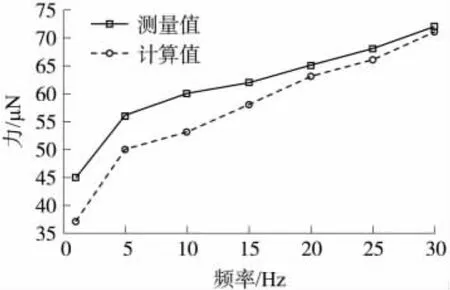
图5 动态微力幅值的测量结果

实验结果表面，由HMPF测定的动态微力的幅值和理论值之间有一定程度的误差，主要原因是:悬臂梁结构的HMPF自由端受力弯曲后，压电陶瓷极化部分受到拉伸时，在电极表面产生电荷;当HMPF被拉伸到最大位置时，电荷量最大。当压电陶瓷极化部分受到回复拉力时，在电极表面将产生和拉伸时相反的异种电荷，并和原来的电荷相互抵消，且由于HMPF的电容很小，原来的电荷将很快消失，导致HMPF的电荷很快减小到零;而此时，HMPF并未回复到平衡位置，其应变还是正应变，电荷和应变相比有滞后。在接下来的回复和压缩过程中，HMPF的电荷和应变之间同样有滞后。由于HMPF产生的电荷和所受到的力之间存在滞后，导致动态微力幅值的测量值和理论值之间有误差。

随着激励频率的增加，HMPF压电陶瓷极化部分受到拉伸和压缩的转换过程加快，电荷泄漏减少，产生的电荷和所受到的力之间的滞后减小，动态微力幅值的测量值和理论值之间的误差也逐渐减小。

从测量结果看，HMPF测量的动态微力的频率值和理论值误差不大，主要原因是:HMPF在测量过程中电荷的滞后主要是幅值的滞后，频率滞后很小，所以频率的测量值和理论值较为接近。

3 结论

悬臂梁结构HMPF自由端受到动态微力作用后，电极上将产生交变电荷。本文基于第一类压电方程和悬臂梁弯曲振动理论，使用平均电荷方法，推导了悬臂梁结构HMPF自由端受到动态微力作用时，电极上产生电荷的解析表达式。分析了长度和半径比对产生电荷的影响，结果表明含铂金芯的

HMPF传感器具有最佳半径比。搭建了HMPF动态微力传感器实验系统，进行动态微力传感实验;实验结果表明，悬臂梁结构HMPF对于动态微力具有很好的传感特性，可以较准确地测量动态微力的频率和幅值。该理论模型将进一步促进HMPF传感器的研究和应用。

［1］Gael Sebald，Jinhao Qiu，Daniel Guyomar，et al.Modeling and Characterization of Piezoelectric Fibers with Metal Core［J］.Japanese Journal of Applied Physics，2005，44(8):6156－6163.

［2］QiuJinhao，Yamada N，JunjiTani，etal.Fabrication of Piezoelectric Fibers with Metal Core［C］//Proc.Of SPIE’s 10thInternational Symposium on Smart Structures and Materials，Active Materials:Behavior and Mechanics，D.C.Lagoudas，Ed.，San Diedo，CA.，Vol.555053:475－483，2003.

［3］Hiroshi Sato，Tadashi Sekiya，Masaru Nagamine.Design of the metal-core piezoelectric fiber［C］//Proceedings of SPIE，Smart Structures and Materials 2004:Smart Structures and Integrated Systems，Vol.5390:97－103(SPIE，Bellingham，WA，2004).

［4］Gael Sebald，Jinhao Qiu，Daniel Guyomar.Modelling the Lateral Resonance Mode of Piezoelectric Fibers with Metal Core［J］.Journal of Physics D:Applied Physics J.Phys.D:Appl.Phys.38(2005)3733－3740.

［5］Gael Sebald，Abdelmjid Benayad，Qiu Jinhao，et al.Electomechanical Characterization of 0.55Pb(NiNb)O－0.45Pb(Zr0.3Ti0.7)O3 Fibers with Pt Core［J］.Journal of Applied Physics，2006，100:054106－1－6.

［6］Hiroshi Sato，Masaru Nagamine.Mechanical properties of metalcore piezoelectric fiber［C］//Proc.of SPIE，Smart Structures and Materials 2005:Smart Structures and Integrated Systems，Vol.5764:623－629(SPIE，Bellingham，WA，2005).

［7］Kiyoshi Takagi，Hiroshi Sato，Muneharu Saigo.Robust Vibration Control of the Metal-Core Assisted Piezoelectric Fiber Embedded in CFRP Composite［C］//Proc.of SPIE，Smart Structures and Materials 2004:Smart Structures and Integrated Systems，Vol.5383:376－385(SPIE，Bellingham，WA，2004).

［8］Kiyoshi Takagi，Hiroshi Sato，Muneharu Saigo.Damage Detection and Aain-Scheduled Control of CFRP Smart Board Mounting the Metal Core Assisted Piezoelectric Fiber［C］//Proc.of SPIE，Smart Structures and Materials 2005:Modeling，Signal Processing，and Control，Vol.5757:471－480(SPIE，Bellingham，WA，2005).

［9］Davood Askari，Hiroshi Asanuma，Mehrdad N，et al.A Comparative Study on Macro-Fiber Composites and Active Fiber Composites with Metal-Core Piezoelectric Actruators/Sensors［C］//Proc.Of SPIE，Smart Structures and Materials 2006，Vol.6170:6170|－1－6170|－12.

［10］Sato H，Sekiya T，Shimojo Y.Fabrication and Vibration Suppression Behavior of Metal Core-Piezoelectric Fibers in CFRP Composite［C］//Proc.of TRansducing Materials and Devices，Brugge，Belgium，Vol.4946:80－87，2003.

［11］常伟杰，刘建，季宏丽，等.含金属芯压电纤维对Lamb波传感实验研究［J］.压电与声光，2010，32(5):797－810.

［12］刘建，裘进浩，常伟杰，等.基于含金属芯压电纤维与Lamb波的一维结构损伤定位研究［J］.振动与冲击，2011，30(4):16－20.

［13］Qiu Jinhao，Majung Park，Daisuke Hoshi，et al.The Research of the Development of the Air Flow Sensor Using the Piezoelectric Fiber with Pt Core［J］.Japan AEM，2004，12(4):299－303.

［14］Bian Yixiang，Qiu Jinhao，Wang Xinwei.The Constitutive Equations of Half Coated Metal Core Piezoelectric Fiber［J］.International Journal of Applied Electromagnetics and Mechanics，2009，29(1):47－64.

［15］边义祥，裘进浩，王鑫伟，等.半电极含金属芯压电纤维的驱动性能［J］.光学精密工程，2009(1):107－117.

［16］Jan G Smits.Dynamic Admittance Matrix of Piezoelectric Cantilever Bimorphs［J］.Journal of Microelectromechanical Systems，1994，3(3):105－112.

［17］Dongchang Sun，Liyong Tong，Satya N Atluri.Effects of Piezoelectric Sensor/actuator Debonding on Vibration Control of Smart Beams［J］.International Journal of Solids and Structures，2001，38:9033－9051.