Sigma-Delta微加速度计非理想因素建模与系统级设计*

刘云涛，王 颖

(1.哈尔滨工程大学信息与通信工程学院，哈尔滨 150001;2.中国科学院微电子研究所，北京100029)

加速度计是一种可以将加速度物理信号转化成能够测量的电信号的仪器，具有μgn水平的高精度加速度计被广泛应用于导航、制导、空间微重力测量，以及自动化工业中［1－3］。随着 MEMS技术的发展，以及硅微加速度计的商业和军事价值的提高，电容式微加速度计成为微机电系统领域和微传感器领域内研究热点［4］。

高性能的微机械加速度计通常利用静电力反馈方式提高系统的灵敏度、线性度、带宽和动态范围［5］，静电力反馈方式可分为模拟反馈和数字反馈。Sigma-Delta(ΣΔ)调制器是实现数字静电力反馈系统的最有效方式。在微机械加速度计中，敏感结构的机械带宽通常较窄，因此可以很容易地获得很高的过采样率(OSR)，从而有效地抑制噪声，提高传感器系统性能。相比于模拟反馈方式，ΣΔ调制技术可以提供直接的数字输出，采用一位数字反馈可以大大降低静电力非线性问题，更为重要的是这种方式消除了模拟反馈中由于质量块偏离严重而产生的静电力吸引问题，大大提高了系统可靠性［6］。

然而，闭环ΣΔ微加速度计系统是一个非常复杂的混合信号反馈系统，它的模块工作在多个域下，包括机械的和电学的，连续时间和离散时间的，模拟和数字的，线性和非线性的。另外，系统中机械的和电学的非理想因素的存在对系统性能都会产生影响，所有这些都使得模拟和仿真整个闭环系统变得非常复杂。虽然如此，对包含非线性及非理想因素的系统的仿真分析对于确定系统中主要参数对性能的影响，为传感器设计提供指导和验证性能极为重要。本文将分析微加速度计系统中的主要非理想因素，建立非理想因素的模型，并在此基础上，采用Matlab的Simulink工具进行ΣΔ微加速度计系统级设计，为微加速度计接口电路设计和传感器整体性能优化提供指导。

1 ΣΔ微加速度计基本结构

ΣΔ微加速度计就是利用ΣΔ调制技术实现数字闭环反馈的，随着微机电系统技术的发展，ΣΔ调制技术被引入到微机械传感器设计中。由于微加速度计的敏感结构可以看作质量－弹簧－阻尼的振动系统，具有二阶传输特性，其传输函数如式(1)所示［7］:

该传输函数具有两个极点和低通频率响应特性，如果把敏感结构包围在反馈环中，敏感结构就起到二阶积分器作用，进而可以作为ΣΔ调制器中的积分器。图1是闭环ΣΔ微机械加速度计的基本结构，敏感结构除了提供差分电容变化检测外加加速度信号外，还可利用其二阶低通特性在闭环系统中起到噪声整形的作用。

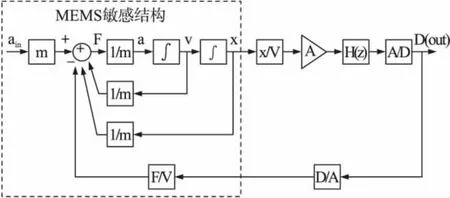
图1 闭环微机电ΣΔ加速度计的基本结构

与机械结构接口的前端电路检测差分电容变化，并转换为电压输出，因此其噪声性能和灵敏度对于整个系统性能至关重要。环路滤波器H(z)对两极点的敏感结构提供补偿，确保系统具有足够的稳定裕度，同时H(z)也可以通过插入电学积分器提供额外的噪声整形，成为高阶结构调制器。调制器的阶数定义为系统开环传输函数的极点个数，由于敏感结构具有两个极点，因此仅以敏感结构作为积分器的调制器为二阶结构，如果环路中含有L个电学积分器，则该调制器的阶数为L+2。在微机电ΣΔ调制器中，系统的阶数仅表明前置通路的极点个数，并不能反映噪声整形的能力。

为了获得更好的信噪比、更低的噪声密度，通常在环路滤波器中采用级联积分器构成高阶调制结构。然而对于高阶结构，增加的极点导致系统相位迅速衰减，产生了稳定性问题。

2 非理想分析与建模

在ΣΔ微加速度计系统中存在着各种机械的和电学的非理想因素，这些非理想因素主要包括敏感结构固定电极运动、时钟抖动、开关热噪声、运算放大器噪声。

2.1 固定电极运动

电容式微加速度计中，活动电极在外力作用下发生位移而产生差分电容变化。事实上，除了活动电极运动外，在外力作用下，固定电极也会产生运动，对系统引入了误差。

感应模式下，在外加加速度作用下，固定电极的偏移量是非常小的，因为作用在电极上的力等于电极质量与加速度的乘积，该值远远小于作用在质量块上的力。然而在反馈模式下，由于静电力是相互吸引的作用，作用在电极和质量块的力是相等的，此时电极的位移量就只由自身的刚性决定。

当有外加力作用时，质量块产生了位移量为y的偏移，固定电极的上下极板受到的静电力分别为:

式中，ε为介电常数，A为固定电极和活动电极两极板的重合面积，d0为固定电极和活动电极的初始距离，vr为施加在固定极板的高频激励信号，Vfb为施加在敏感电容中间极板的反馈电压。

敏感质量块受到的静电力为:

因此在闭环系统中，考虑上下电极在静电力作用下产生形变的敏感结构数学模型如图2所示，图中mm为敏感质量块质量，mc为上下电极质量，km为机械弹簧弹性系数，kc为极板的弹性系数。

图2 考虑固定电极运动的敏感结构模型

2.2 时钟抖动

时钟信号本身存在相位噪声，而相位噪声会造成时钟信号的上升沿和下降沿的瞬间不确定，从而导致采样时刻的不确定，这种采样时刻的不确定性就称作时钟抖动［8］。时钟抖动会导致采样不均匀，使量化器输出的量化误差功率提高。由于开关电容电路是一个采样数据系统，在每个时钟周期内实现采样电容与积分电容之间的电荷转移，所以一旦模拟信号被采样，时钟信号的波动是不会对电路性能产生影响的，因此时钟抖动对开关电容电路的影响仅仅是发生在对信号的采样时刻，也就意味着时钟抖动与调制器的结构和阶数都没有关系。

在ΣΔ微加速度计中，采样电容为敏感结构的可变电容，输入信号为加速度信号，根据微加速计信号检测原理，接口电路前端电荷积分器的输出为

式中C0为敏感结构静态电容，Cf为接口电路前端电荷积分器的反馈电容。采样开关导通时对驱动信号vr的采样过程就等效于对加速度信号a的采样，因此时钟抖动的作用可表示为对输入信号a的影响。

时钟抖动误差是抖动统计特性和调制器输入信号的函数，假设输入是幅值为A，频率为fin的正弦信号x(t)，采样频率为fs，且采样时间的误差是δ，则产生的误差为

这样当存在时钟抖动时信号的实际输入为:

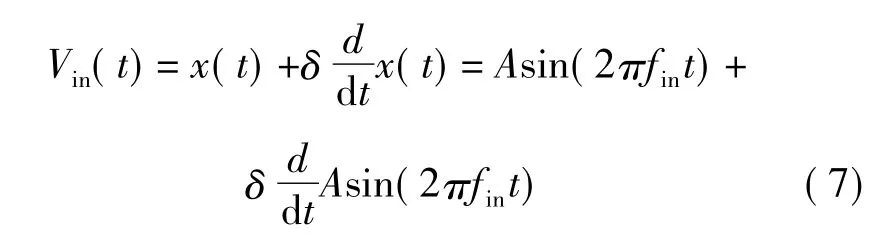
根据式(7)，含有时钟抖动的输入信号模型如图3所示。

图3 时钟抖动模型

2.3 开关热噪声

热噪声是由于载流子的随机热运动引起的，热噪声属于宽带白噪声。采样开关热噪声由开关电容的时间常数和运放的带宽决定，在每一次采样过程中，开关热噪声也同时被采样到采样电容上，引起输出误差。对于一个导通电阻为Ron的开关，被采样到采样电容上的总的热噪声可表示为［9］:

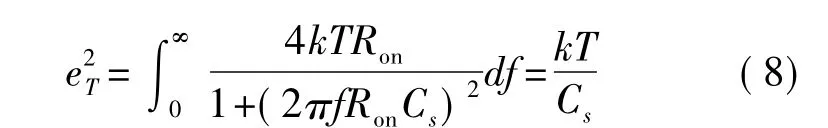
k为波尔兹曼常数，T为绝对温度，4kTRon为开关导通电阻的噪声功率密度。开关热噪声也直接叠加在输入信号上，因此受开关热噪声影响的输入信号为:

这里n(t)表示高斯随机分布，根据式(9)含有开关热噪声的输入信号模型如图4所示。

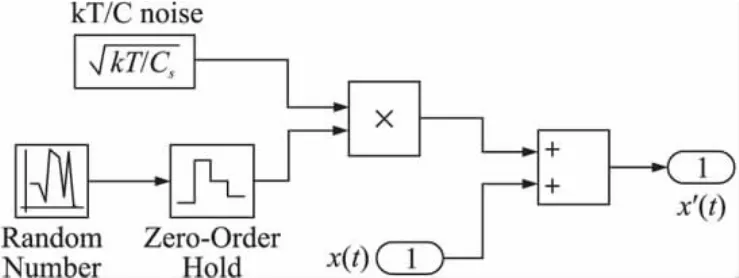
图4 含有开关热噪声的输入信号模型

2.4 运算放大器噪声

运算放大器噪声是系统的主要噪声源，在传感器接口电路的设计中采用相关双采样或斩波稳定技术，可以有效地降低1/f噪声和运放失调，因此运算放大器的噪声主要为运放的热噪声，运算放大器的热噪声可表示为

b为采样过程中噪声折叠导致的放大倍数，Vn为运放的输入参考热噪声

如果用一个随机信号产生噪声，运算放大器噪声的模型如图5所示。

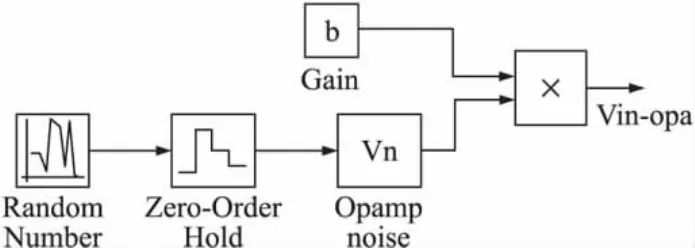
图5 运算放大器噪声模型

3 ΣΔ微加速度计系统设计

ΣΔ调制器主要包括三种结构:单环结构、前置求和结构(interpolative结构)、级联结构(MASH结构)［10－11］。单环结构是最适用于微机械力平衡反馈系统的结构方式。由于敏感质量块的运动速度是不可控的，并且传感器输出是一个非常微弱的信号，由于噪声注入的影响，感应节点处的反馈是不希望存在的，因此带有多路反馈的interpolative结构不适用。另一方面，微加工制作的传感器具有很大的不确定性，加工过程中温度、空气中电荷以及其它环境因素都可能对敏感结构性能产生影响。因此在设计阶段，传感器的特性还不确定，其二阶量化噪声整形能力依赖于其结构参数，因此依靠精确的量化噪声消除方式的MASH结构也不适用。

基于以上原因，本文采用单环结构进行系统设计。ΣΔ微机械加速度计系统由信号输入、敏感结构、增益、环路滤波器、反馈等部分组成。信号输入部分包含了时钟抖动和采样开关热噪声;敏感结构由质量块和上下电极三个传输函数构成;增益为质量块位移到电荷积分器的输出电压增益;环路滤波器包括前置补偿和电学积分器。结合前文中分析的非理想因素及所建立的模型，并考虑机械噪声，所设计的四阶ΣΔ微加速度计系统的Simulink模型如图6所示，如果将该图中的电学积分器部分去掉，该系统就变为二阶ΣΔ加速度计系统。

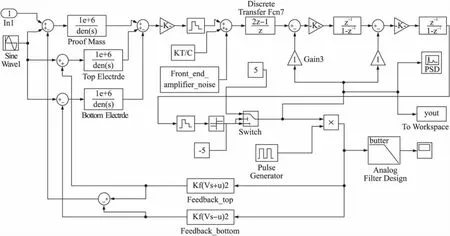
图6 微机械ΣΔ加速度计系统的Simulink模型

4 仿真结果与分析

在该系统中，假设时钟抖动为10 ns，开关热噪声为10 nV/Hz1/2，运放输入热噪声为50 nV/Hz1/2，固定极板的弹性系数为2 000 N/m，前置补偿系数α=0.5，积分器增益b1=b2=0.5。输入为幅值±1 gn、250 Hz正弦信号，在256 kHz采样频率、128倍过采样率(OSR)下，二阶和四阶ΣΔ微加速度计的输出频谱如图7所示。

图7 微机械ΣΔ加速度计Simulink仿真输出频谱

由仿真结果可知，四阶结构的信号－噪声－谐波失真比(SNDR)为92.7 dB，有效位(ENOB)为15.10位。二阶结构SNDR为70.1 dB，ENOB为11.36位，很显然该值远低于ΣΔ调制器的理论计算值。对于采用1位量化的调制器，其系统本身具有很高的线性度，因此SNDR的损耗主要由高量化噪声造成。在这里敏感结构虽然具有两个极点，但这两个极点都位于谐振频率附近，因此其提供的噪声整形能力非常弱。另外，从图7可以看出，二阶和四阶结构的频谱带宽外噪声和频率的关系分别为30 dB/dec和50 dB/dec，该值分别相当于1阶以及二、三阶之间ΣΔ调制器的噪声整形能力。在二阶结构的频谱图中，在信号的倍频点出现很多谐波(tones)，这说明量化器的输出和输入信号相关性很高，量化噪声不再是白噪声。而四阶结构由于额外的电学积分器加入，使得量化噪声被随机分布在整个频带内，消除了谐波。

为了验证所建立模型在电路优化中的作用，采用0.5 μm CMOS工艺完成了二阶和四阶ΣΔ微加速度计接口电路的晶体管级设计［12］，并利用敏感结构的Spice模型进行仿真，晶体管级电路与系统级的Simulink模型中取相同的参数。图8为二阶和四阶系统的晶体管级Hspice仿真结果，结果表明二阶系统的SNDR为68.5 dB，ENOB为11.1位，四阶系统的SNDR为89.2 dB，ENOB为14.5位。可见基于本文所建立的系统中非理想模型的系统级仿真结果与整体传感器的晶体管级仿真结果极为接近，而相比于Simulink的仿真，采用Hspice的电路级仿真需要消耗漫长的仿真时间，因此，本文所建立的系统模型可以大大简化传感器的参数优化过程。

图8 微机械ΣΔ加速度计晶体管级Hspice仿真输出频谱

5 结论

本文考虑了电容式ΣΔ微加速度计中的敏感结构固定极板运动、时钟抖动、开关热噪声、运算放大器噪声等非理想因素，建立了适用于Simulink环境仿真的模型，并在此基础上完成了一种单环结构的ΣΔ微加速度计系统级设计和仿真。仿真结果表明，本文所建立的模型可以准确的表现出系统的性能，并可以大大缩短仿真时间，简化系统优化过程。

［1］Lee W F，Chan P K.A Capacitive-Based Accelerometer IC Using Injection-Nulling Switch Technique［J］.IEEE Transactions on Circuits and Systems，2008，55(4):980－989.

［2］郑旭东，曹学成，郑阳明.一种电容式微机械加速度计的设计［J］.传感技术学报，2008，21(2):226－229.

［3］谭晓昀，雷龙刚，王冠石.电容式微机械陀螺双环路闭环驱动电路研究［J］.传感技术学报，2010，23(10):1449－1453.

［4］张灵霖，车录锋，李玉芳.基于阶跃响应的加速度计Q值测试方法研究［J］.传感技术学报，2009，22(10):1417－1421.

［5］Aaltonen L，Halonen K.Continuous-Time Interface for a Micromachined Capacitive Accelerometer with NEA of 4 μg and Bandwidth of 300 Hz［J］.Sensors and Actuators，2009，154:46－56.

［6］KulahH，Chae J，YazdiN，etal.Noise Analysisand Characterization of a Sigma-Delta Capacitive Microaccelerometer［J］.IEEE Solid-State Circuits，2006，41(2):352－361.

［7］Krishnan G，Kshirsagar C U.Micromachined High-Resolution Accelerometers［J］.J of Indian Institute of Science，2007，87(3):333－361.

［8］Choop P M，Hamoui A A.Analysis of Clock-Jitter Effects in Continuous-Time ΔΣ Modulators Using Discrete-Time Models［J］.IEEE Trans on Circuits and Systems，2009，56(6):124－128.

［9］Suarez G，Jimenez M，Fernandez F O.Behavioral Modeling Methods for Switched-Capacitor ΣΔ Modulators［J］.IEEE Trans on Circuits and Systems，2007，54(6):1236－1244.

［10］Chao K C H，Nadeem S，Lee W L，et al.A Higher Order Topology for Interpolatative Modulators for Oversampling A/D Conversion［J］.IEEE Trans on Circuits and Systems，1990，4(3):309－318.

［11］Yin G，Sansen W.A High Frequency and High-Resolution Fourth-Order Sigma-Delta A/D Converter in BiCMOS Technology［J］.IEEE J of Solid-State Circuits，1994，29(8):857－865.

［12］Liu Y T，Liu X W，Chen W P.Design and Noise Analysis of a Sigma-Delta Capacitive Micromachined Accelerometer［J］.半导体学报，2010，31(5):550061－550066.