三齿轮联动双曲柄四环板式针摆行星传动的动力学研究*
2011-10-20鲍君华何卫东
鲍君华 何卫东
(大连交通大学机械工程学院,辽宁大连 116028)
摆线针轮行星传动以其传动比范围大、结构紧凑、传动效率高等一系列优点在各个工业领域得到了广泛的应用[1]。而新型的三齿轮联动双曲柄四环板式针摆行星减速器除具有传统摆线针轮传动的优点外,还克服了传统结构因转臂轴承在行星轮内尺寸和承载能力受限制及输出机构为悬臂支撑刚度小等缺点,充分发挥了针摆行星传动的传动能力,同时相对于渐开线三环减速器又具有同时啮合齿数多、啮合角小、传动比范围大、齿面硬度高等优点。但由于结构的特点和产品基本参数的不确定性,因此为提高减速器工作性能和品质,改善减速器振动特性,降低运行噪声,通过改进设计对此型传动的基本参数进行了优化,分别形成了采用直齿轮和斜齿轮作为第一级减速机构的新样机。但随着承载能力、输入轴转速的提高,及传动基本参数的修改,对各型样机的试验验证将消耗大量的财力和物力,同时对于新产品的开发设计也是不经济的,因此有必要在设计阶段对产品的动力学性能进行分析验证。
根据三齿轮联动双曲柄四环板式针摆行星传动的工作原理绘制其结构简图,如图1所示。其工作原理为:输入轴带动主动齿轮驱动两曲柄轴上的从动齿轮转动,以保证两曲柄轴在传动过程中同步转动,从而实现平行四边形机构中两个曲柄轴的整周同步回转;而在两曲柄轴之间通过转臂轴承联接的四片环板形成了四组平行四杆机构的连杆,这些连杆两两相位相差180°,并通过其上的针齿与输出轴上的摆线轮轮齿啮合完成减速传动。经过系统全面的理论分析和设计计算,依据减速器生产图纸在Pro/E软件系统中完成关键零部件的实体建模和虚拟装配工作,并将装配好的模型导入ADAMS软件系统中进行动力学仿真分析。
1 减速器的实体建模及虚拟装配
1.1 齿轮及摆线轮的参数化建模
改进的样机分别采用相同齿数和传动比的直齿轮和斜齿轮两种传动方案。为方便建模提高工作效率,将模型中齿轮所采用的变位直齿和斜齿圆柱齿轮的基本参数,包括:齿数Z、法面模数mn、法面齿顶高系数、法面顶隙系数、法面压力角αn、分度圆螺旋角β、法面变位系数xn、齿宽b及齿顶高削弱高度Yt等齿轮基本参数通过设置交互式参量的形式带入Pro/Engineer软件系统中,实现对应零件实体模型的参数化建模[2]。
对于齿轮的渐开线螺旋曲面的建立,首先以齿轮的法面基本参数为基础,生成齿轮的端面渐开线曲线。对于具有变位要求的斜齿轮其在分度圆上的齿槽宽et和齿厚st变位后对应弧长会产生变化,考虑变位系数xn对尺寸的影响,通过合理设置变位后的齿槽宽et生成完整的渐开线齿槽齿廓形状[3],对于文中涉及到的直齿轮可直接设置其螺旋角β=0°;然后,根据软件系统的建模特点,共生成了3条分度圆柱面上的螺旋线作为轨迹曲线,其中1条作为主轨迹曲线,另外2条作为辅助轨迹曲线,它们的轨迹方程完全相同,只是曲线的起始参照点选在不同的位置,在柱面坐标系下由螺旋线的极坐标参数方程绘制出空间螺旋线,并沿螺旋线方向进行渐开线螺旋曲面拉伸,最终形成渐开线齿轮的实体模型。
对于摆线轮齿形的建模,在Pro/Engineer软件系统下采用摆线轮在直角坐标系下的参数方程构造摆线轮的参数化模型。而实际应用摆线针轮行星传动时,为补偿制造误差,便于装拆和保证润滑,摆线轮齿与针轮齿之间必须有啮合间隙。因此,实际的摆线轮齿形不采用标准齿形,必须进行修形。本文引入等距修形量Δrrp和移距修形量Δrp两个加工参数,得到经优化的新齿形以便更真实地模拟样机的啮合过程和工作特点。
1.2 虚拟样机的装配
由于减速器的结构特点,作为提供行星运动的各个转臂轴承自身的结构特点和振动特性将对整个传动系统造成影响,为更准确地反映样机的动力学特性,本文中同样对转臂轴承进行了模型的建模和虚拟装配,并最终装配进整个减速器模型中,根据转臂轴承内外圈的具体尺寸和滚动体的尺寸和数量形成的装配模型如图2所示。

最后按照样机设计图纸的尺寸要求完成包括主从动齿轮、摆线轮、环板、减速器箱体等样机主要零部件的三维实体模型后,根据各个零件之间的相互装配及位置关系分别形成包括曲柄轴系、环板组件系、输出轴系、齿轮传动系统等几个基本部件模型,并与箱体进行最后的配合和定位关系的装配,形成的装配模型如图3所示。
2 动力学模型的建立
2.1 模型的导入及物理特性设定
将在Pro/Engineer软件中经装配完成后的模型导入ADAMS软件系统中。由于装配模型实体数量过多,同时为尽量减小动力学模型的计算规模,提高计算分析效率,对导入的模型进行整合,对于没有相对运动关系的各部件内的实体零件进行Merge合并操作,从而减少零件的数目,方便模型的建立。由于零件主要材料均为碳钢和铸铁,所以选择软件系统自有的Steel材质对零件进行材料定义,并由系统自动生成质心参考点和质量、惯量等物理数据;同时根据模型在参考空间内的放置位置重新设置系统重力场方向,以模拟零件自重对系统动力学特性的影响。最后模型共包含Solid实体574个,Part零件19个。
2.2 动力学模型的建立
为准确模拟样机的动力学特性,模型的关键是对以下几部分零件间的运动副关系进行定义,包括:3个齿轮间的啮合接触关系,曲柄轴及环板分别与转臂轴承及各滚动体之间的接触副关系,4片环板上的针齿套和摆线轮轮齿之间的接触关系等;以上接触副均采用软件自定义的Solid to Solid接触副,以形成样机的非线性动力学系统的基础,模型中共生成624对接触副。
对于模型上静止零部件,如箱体、齿轮箱等零件采用Fixed运动副与系统Ground相固联。为减小模型计算量,提高设计计算效率,对包括输入轴、曲柄轴、输出轴的轴系零部件的轴承支撑结构进行简化,不设置具体轴承结构所形成的滚动体和内外滚道间的接触副,而采用简单的Revolute定轴转动副,以约束各轴系零件绕轴承孔作定轴转动的同时,进行动力和运动的传递。最后形成的样机模型如图4所示。

本文对分别采用直齿轮和斜齿轮作为第一级减速装置的两种虚拟样机分别进行装配并导入ADAMS软件中进行动力学模型的建模[4],分别对各自在额定转速下的空载和满载动力学特性进行了仿真运算。因此,首先设置小齿轮所在的输入轴转速为电动机额定转速n1=1 500 r/min,通过主从动齿轮、环板、摆线轮等零件之间的接触将运动和动力传递至输出轴。同时,为模拟样机在满载工作条件下的工作状态,本文在输出轴上施加与输出轴转向相反的恒定满载转矩,为更好地完成仿真计算,避免过大的启动冲击,在进行转矩的施加时采用分段加载,使转矩逐渐达到满载,载荷采用 Step 函数施加,表达式为 Step(time,0,0,0.01,0)+Step(time,0.01,0,0.05,-8 163.88),力矩单位为N·mm,空载时相当于转矩为0 N·mm。
3 仿真结果对比分析
3.1 仿真运行结果
设置仿真运行时长为0.5 s,步长为0.1 ms/步,经仿真计算得到各型虚拟样机在各自工况条件下的计算结果。对采用直齿轮的样机,在空载条件下模型输出轴的平均转速n2≈25.827 4 r/min,仿真分析的平均传动比i仿真≈58.077 9与理论上机构的总传动比i总≈58.285 7之间的传动比误差为0.36%;而在满载转矩条件下的模型输出轴的平均转速n'2≈25.751 3 r/min,仿真分析的平均传动比i仿真≈58.249 5与理论上机构的总传动比i总之间的传动比误差为0.06%。通过比较传动比计算结果,仿真模型较好地反映了样机的运行规律。
对于采用3个斜齿轮作为第一级减速机构的虚拟样机模型,在空载条件下得到的输出轴平均转速n2≈25.805 6 r/min,计算得到仿真分析的平均传动比i仿真≈58.126 9与理论上机构的总传动比i总之间的传动比误差为0.27%,而机构满载条件下的输出轴的平均转速n'2≈25.790 2 r/min,仿真分析的平均传动比i仿真≈58.161 6与理论上机构的总传动比i总之间的传动比误差为0.21%,同样满足传动比的误差要求。
以上结果可以作为检验虚拟样机正确与否的基本依据。
3.2 动力学性能分析
通过对模型中各主要零部件的角加速度计算结果进行傅里叶变换得到其模态特性曲线,虽然本文对采用直齿轮和斜齿轮2种不同驱动方式的样机均进行了计算,但从计算结果分析,各种工况条件下零件的模态频率在数值上基本相同,只是各自振幅幅值有所差异,满载工况条件下角加速度幅值较空载状态下更大。因此本文重点讨论2种形式的样机在满载工况下表现出来的频谱特征。
本文主要对包括由从动齿轮、偏心套等零件所组成的曲柄轴系组件,由转臂轴承、环板、针齿等零件组成的环板系组件和包含摆线轮、输出轴等零件在内的输出轴系组件的仿真计算结果进行了傅里叶变换,得到了他们的转角特性曲线如图5~7所示[5]。
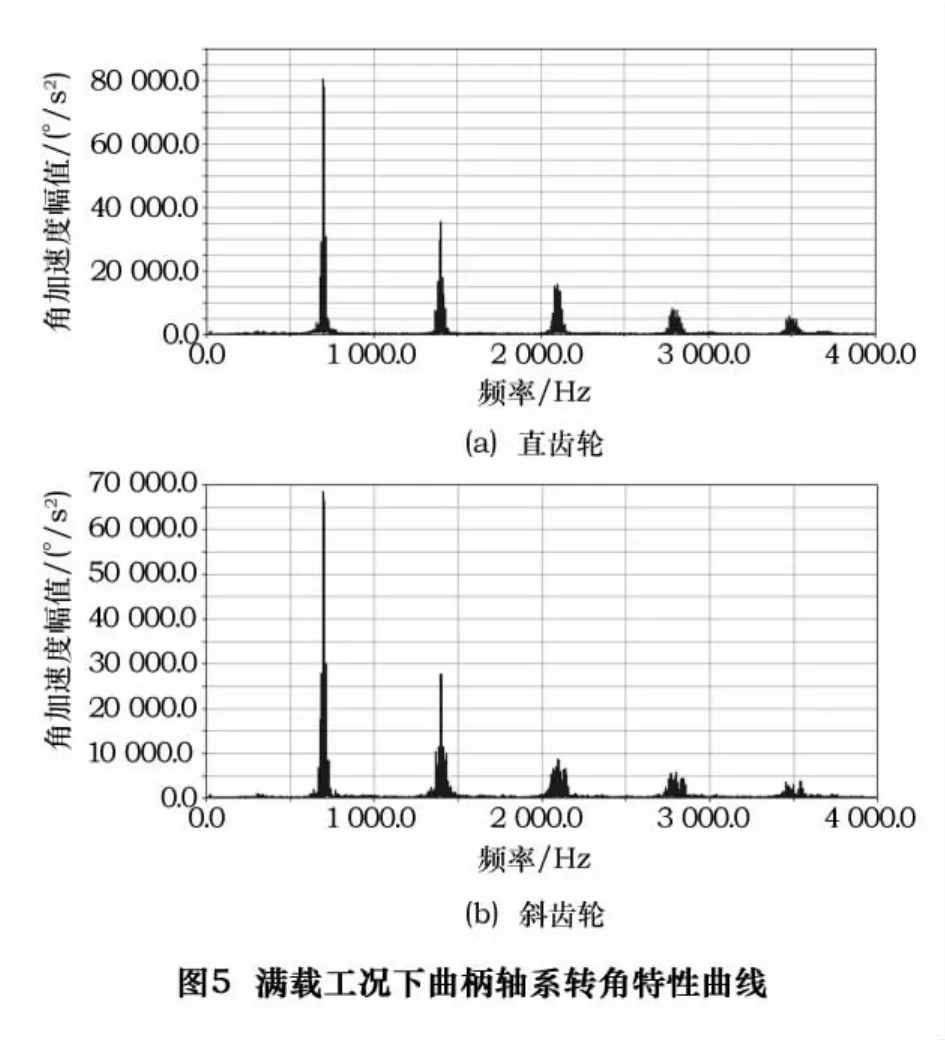
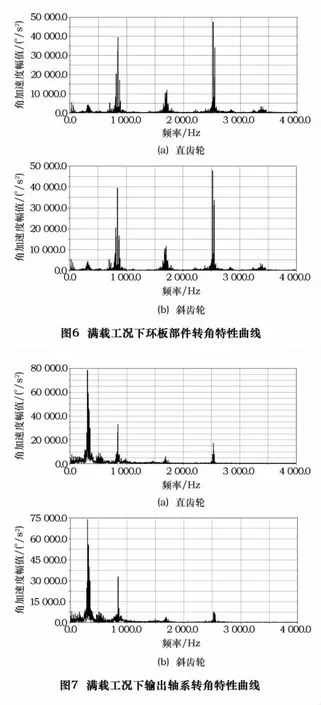
对于曲柄轴系主要选取了5个频率点,其第一阶频率数值在700 Hz的振幅具有最大值,对于直齿轮条件下其幅值为80 738°/s2(图5a),而斜齿轮条件下幅值略有减小为68 609°/s2(图5b),其余各阶频率和幅值分别见图5所示;对环板系组件本文中主要分析了4 000 Hz以内的3个频率点,其中第三阶频率值在2 523 Hz的振幅具有最大值,对于直齿轮条件下其幅值为4 751°/s2(图6a),而斜齿轮条件下幅值略有增大为4 793°/s2(图6b),其余各阶频率和幅值分别见图6;对输出轴组件本文主要分析了4 000 Hz以内的3个频率点,其中第一阶频率值在309 Hz的振幅具有最大值,对应于直齿轮条件下其幅值为7 867°/s2(图7a),而斜齿轮条件下幅值略有减小为7 390°/s2(图7b),其余各阶频率和幅值分别见图7。
通过以上3组主要零部件的模态分析,其振动频率范围均较宽,但主要振动特性还是集中于1 000 Hz以下,对比直齿轮和斜齿轮两种传动方案,由于齿轮的质量和刚度对整机的物理特性的影响较小,所以两种形式样机的响应频率相近,只是对于斜齿轮传动形式与直齿轮传动形式相比较;除环板部件外,对于曲柄轴承和输出轴承来说所对应的幅值有一定程度的减小,主要是因为斜齿轮比直齿轮具有更好的啮合特性,因此选择斜齿轮作为成型产品的传动形式应该是比较理想的选择。
4 样机试验对比
为验证动力学样机模型的精确程度,结合已进行了的三齿轮驱动双曲柄四环板式针摆行星减速器样机的各项动力学测试试验,对仿真分析结果和样机测试结果进行对比分析。
4.1 样机测试试验装置
为测试样机的工作性能,样机实验室台架测试系统主要由减速器样机、输入输出端传感器、加载装置、数据采集和分析装置等试验设备组成,由输入输出端的转矩转速传感器进行有关减速器工作性能数据的采集。同时在减速器箱体的相应位置布置振动加速度传感器,对样机工作过程中的振动信号进行采集和分析处理。实验装置如图8所示。

4.2 测试结果分析
由于减速器样机为闭式齿轮箱结构,无法对其内部具体零部件进行振动测试,所以只能在减速器箱体上设置传感器,根据具体的减速器结构特点在测试过程中选择多个位置进行了振动测试。其中比较有代表性的位置选择了曲柄轴支承轴承轴孔轴承盖径向外圆周面上的一点作为测试点设置加速度传感器,即对应曲柄轴系组件的动力学特征进行测试。驱动样机在输入转速为1 470 r/min,满载工况条件下进行带载振动测试,根据现场采集的№133'号传感器振动测试信号经分析处理后绘制出来的频谱图如图9所示。
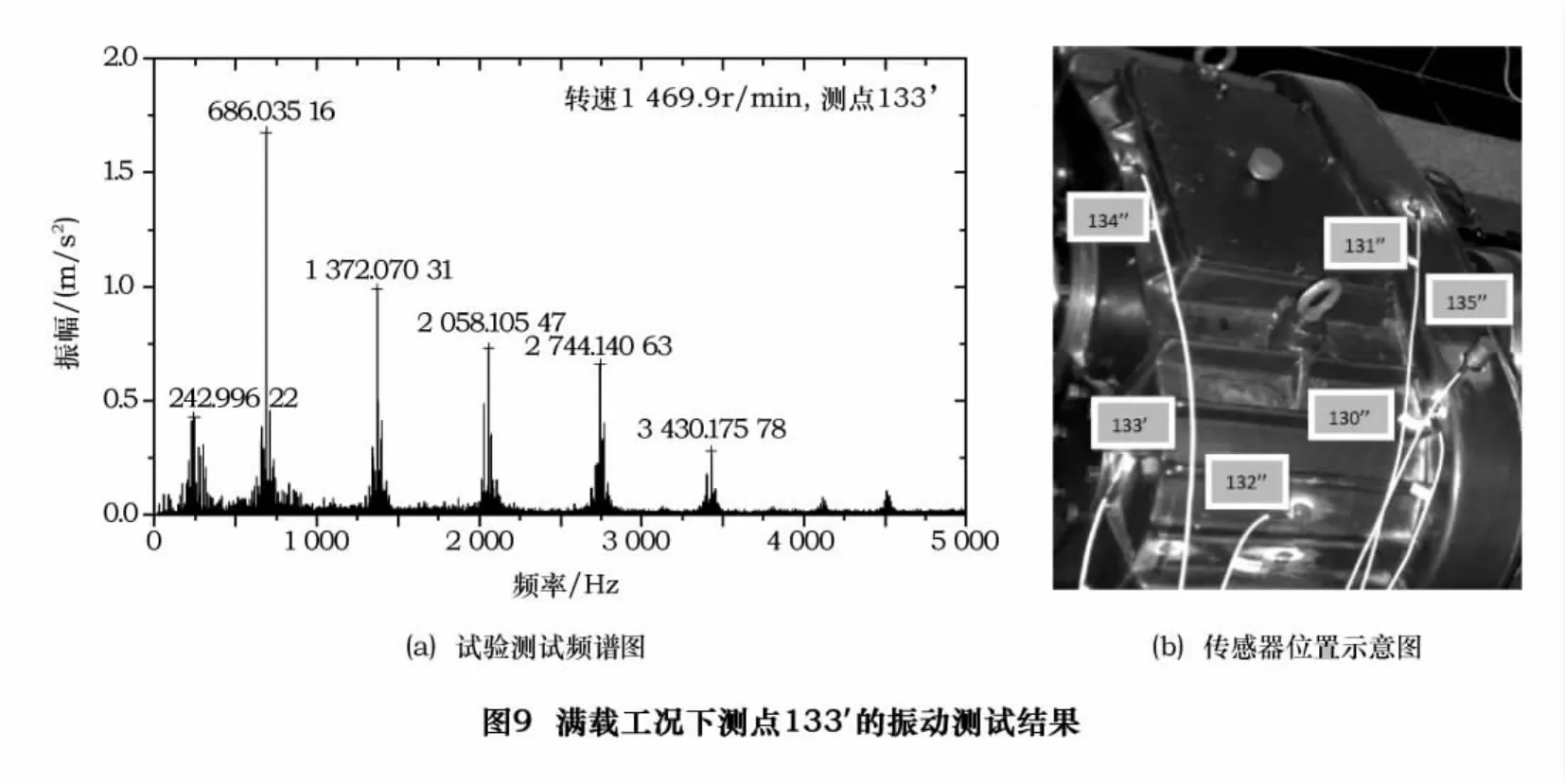
对比图5和图9两种测试分析结果,可以看出虚拟样机动力学分析结果基本体现了实物样机的动力学特性,与实测数据具有相似性,表1中分别列出了由ADAMS软件计算获得的仿真测试结果和样机的实测结果。由测试结果可以看出,曲柄轴在虚拟样机仿真计算和样机实测中的主要响应频率基本吻合,其响应频率与齿轮间的啮合激振频率成倍频关系,其基础频率基本在700 Hz左右。以上对比分析结果同时也反映了虚拟样机模型的正确性和仿真测试方法的可行性。

表1 仿真计算和实测数据对比结果
5 结语
在ADAMS软件环境下完成了2种形式虚拟样机的动力学模型的建模,合理设置了各零件之间的运动副关系,对样机在额定转速下分别对应空载和满载工况条件下的动力学特性进行了运动仿真和分析计算。并结合实验室样机工作性能测试和动力学测试结果,得出以下结论:
(1)在空载和满载条件下,模型所体现出的频谱特性有很大的相似性,同时从传动比的计算结果也比较准确地反映了样机的实际工作特性,因此所建立的虚拟样机模型是真实可信的;
(2)模型中除输出轴系部件外主要零部件在低频下的振动特性并不明显,而对摆线针轮这类主要工作于较低转速下的通用减速器是比较理想的结果;
(3)通过采用虚拟样机技术,不但基本了解和掌握了新型样机的动力学特性,得到了样机运行的仿真动画。其仿真分析结果与实验室样机性能测试和动力学测试结果具有很强的相似性,进一步验证了仿真模型的准确性,提供了一种高效、快捷的新产品测试开发模式。同时也为模型的改进和减速器工作性能的提高提供了良好的设计基础和试验验证工具。
[1]何卫东,李欣,李力行.双曲柄环板式针摆行星传动的研究[J].机械工程学报,2000(5):84 -85.
[2]许洪基,等.现代机械传动手册[M].2版.北京:机械工业出版社,2002:457-461
[3]鲍君华,何卫东,李力行.高速机车牵引齿轮的参数化实体建模及其动力学分析[J].机械传动,2009,33(5):70 -75.
[4]MSC.Software著.MSC.ADAMS FSP 基础培训教程[M].北京:清华大学出版社,2004.
[5]鲍君华,何卫东,史壮.环板式针摆线行星传动的运动仿真及试验对比[J].大连交通大学学报,2008(4):33-36.
