基于最优小波基的轴承故障状态特征提取方法研究*

王 婕 崔玲丽 康晨晖

（北京工业大学机电学院，北京 100124）

轴承发生早期故障时，会产生冲击，但这种局部突变信号很微弱，常被淹没在正常信号中，用传统的傅里叶变换方法很难识别。小波分析作为新兴的数学分支，是一种全新概念的、变分辨率的时频分析方法，即对低频信号有较高的频率分辨率，对高频信号有较高的时间分辨率，特别适用于对时变非平稳信号的分析。

基于小波分析进行轴承故障诊断，已有不少学者进行了此方面研究。如王丽等人通过使用小波变换的分解和重构算法，对具有故障特征的信号进行重构，再通过希尔伯特变换进行解调和细化频谱分析，有效提取出噪声掩盖下的滚动轴承故障特征信号［1］。王楠等利用小波分解的多层次多频带特性和小波重构技术，建立了一种简单、精确和实用的低速重载轴承故障小波分析方法［2］。程军圣等针对滚动轴承故障信号的特点，构造脉冲响应小波，采用连续小波变换的方法来提取滚动轴承故障振动信号的特征［3］。以上方法均是基于小波分解进行故障特征提取，在此过程中，小波基的选择是任意的，而小波基函数具有不唯一性，使用不同的小波基分析同一振动信号效果不同。因而，在降噪及信号特征提取过程中，关键问题在于最优小波基的选取。

本文引入文献［4］提出的SUMVAR这一指标来衡量不同小波基对于分析滚动轴承振动信号的优劣，对不同小波基求其SUMVAR值，认为SUMVAR值最大者为最优小波基;运用最优小波基及其他小波基分别对轴承仿真信号及故障实验信号进行小波降噪，分析降噪信号与原信号的能量比值，降噪信号与原信号标准差，峭度等指标，通过比较，验证所选择的小波基优于其他小波基。再对使用最优小波基的降噪信号做希尔伯特包络解调分析，提取故障特征频率，判断故障发生部位。

1SUMVAR值

SUMVAR（Summation of Variance）顾名思义，是一组方差的和值，通过在某一小波基φm对轴承数据进行4层连续小波变换，得到16个尺度的小波系数，计算同类故障10组数据方差的平均值，求取4类轴承数据平均值的方差，选择前5个最大方差求和即为SUMVAR值。选择最大SUMVAR值的小波为最优小波基，因为SUMVAR值越大，说明方差越大，不同类轴承数据间变动越大，则用该小波辨识不同类别故障的能力就越高［4］。

具体计算步骤如下:

（1）选取外圈点蚀故障、内圈点蚀故障、滚动体点蚀故障和正常4类轴承数据各10组，对每组数据进行4层连续小波变换，计算1～16共16个尺度下的小波系数的方差 si，j，k，其中 i=1，2，3，4 表示不同故障类型，j=1，2，…，10 表示同一类型下不同组数据，k=1，2，…，16表示不同尺度。

（2）计算同类故障10组数据方差的平均值:

（3）求取4类轴承数据平均值的方差:

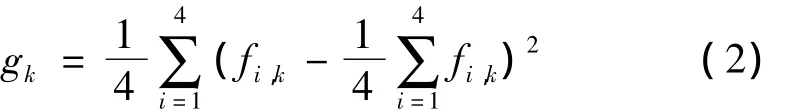
（4）在求得的 gk，k=1，2，…，16 中，选择前5 个最大值求和，得到的和即为SUMVAR值。

选用103个常用小波基计算SUMVAR值，得到计算结果，现将SUMVAR值较大的9个小波基计算结果见表1。

表1 部分小波基SUMVAR值计算结果

经过比较，选择db24为最优小波基。

2 小波降噪原理

对信号去噪实质上是抑制信号中的无用部分，增强信号中有用部分的过程。信号的性质可以用它的小波系数来刻画，小波系数较大者，携载的信号能量较多，小波系数较小者携载的信号能量较少，因此可用携载能量的多少作为衡量小波系数在信号中的权重大小。引入以信号能量为判据的浮动阈值来作为甄别受到噪声污染的小波系数，将等于和小于阈值的小波系数视为零而舍去，把这些值当作噪声处理掉，仅仅用阈值以上的小波系数来重建原信号，既去掉了大部分噪声，又不致于引起重建结果的明显失真。

一般地，一维信号去噪的过程可分为如下3个步骤［6］。

步骤1:一维信号的小波分解。选择1个小波并确定分解的层次，然后进行分解计算。

步骤2:小波分解高频系数的阈值量化。对各个分解尺度下的高频系数选择1个软阈值进行软阈值量化处理。

步骤3:一维小波重构。根据小波分解的最底层低频系数和各层高频系数进行一维小波重构。

阈值的选择是离散小波去噪中最关键的一步，如果阈值太小，则施加阈值后小波系数将包含过多的噪声分量，达不到去噪的效果;反之，如果阈值太大，则去除了有用的成分，造成失真。本文使用默认阈值去噪处理，即使用MATLAB小波分析工具箱中自带函数生成默认阈值，利用其自带函数进行去噪处理。

3 对仿真信号进行小波降噪

［7］给出了轴承外圈单点点蚀故障仿真信号，即:用指数衰减函数与周期脉冲信号卷积模拟产生轴承外圈故障信号。指数衰减函数如式（3）所示，周期性冲击信号其幅值为1，周期为1/fd，其中fd为故障特征频率，取76．88 Hz。采样点数为8 192，采样频率为15 360 Hz。

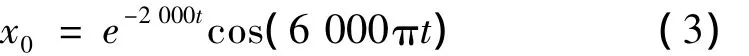
为了更加符合实际信号，对模拟产生的外圈单点点蚀故障振动信号进行染噪，染噪后的信号波形及频谱如图1，分别采用以db24、db15和sym14的小波基进行默认阈值小波降噪处理，处理后的信号波形及频谱如图2～4所示。可以看出，降噪后的周期冲击性更加明显。为了衡量不同小波基的降噪效果，采用如下指标:

（1）降噪信号与原信号的能量比值:

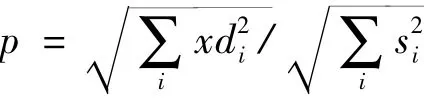
（2）降噪信号与原信号间的标准差:

p值反映了降噪信号保留能量多少，值越大，说明信号降噪以后，保留能量越多。e值反应了降噪后信号与原信号相似度，e越小，降噪信号与原信号相似度越高［5］。峭度指标反映了降噪后信号冲击性能，Kv值越大，说明故障冲击越明显，降噪效果越好。采用p、e、Kv等指标分别对使用 db24、db15、sym14小波降噪后的仿真信号进行分析，分析结果见表2。

表2 使用不同小波基的仿真信号降噪指标计算结果

比较db24与其余两小波降噪指标，虽然峭度值略小于db15及sym14，但是p值均大于db15及sym14，说明经过该小波降噪后保留了更多的能量信息;比较e值发现，db24小波e值均小于其余两小波，说明该小波降噪后，信号与原信号具有更高的相似度。综合以上3指标，说明db24小波是最优小波。

对经过db24小波降噪后的仿真信号做Hilbert包络解调分析，得到解调谱图如图5所示。从图5可以看出在76．88 Hz处出现峰值，以后出现峰值都是该频率的倍频，76．88恰好是设定的外圈故障特征频率，与预想相符，说明本方法是有效的。因此，可以诊断，出现故障为外圈故障。

4 对实验信号进行小波降噪

实验系统由轴承试验台、HG3528A数据采集仪和笔记本电脑组成。其中试验台由三相异步电动机通过挠性联轴器与装有转子的转轴连接，如图6所示。轴由2个6307轴承支撑。轴承点蚀故障大小为0.2 mm。电动机转速R=1 496 r/min，轴承的大径D=80 mm，小径d=35 mm，滚动体个数为Z=8，接触角α=0。依据上述参数计算出轴承外圈故障特征频率为76.88 Hz，内圈故障频率为122．738 Hz，滚动体故障特征频率为51．170 6 Hz，采样频率为15 360 Hz。

使用该试验系统采集外圈故障实验信号，实验信号时域图及频谱图如图7所示。对采集到的实验振动信号分别用db24、db20、sym9小波对其进行默认阈值降噪处理，降噪结果见图8～10。

采用 p、e、Kv等指标分别对使用 db24、db20、sym9小波降噪后的实验信号进行分析，分析结果见表3。

比较db24与db20，虽然p值略小，但db24的e值小于db20，说明db24降噪后信号与原信号具有更高的相似度;db24峭度指标大于db20，说明db24降噪后信号冲击强度更高，降噪效果更好。比较db24与sym9，虽然峭度值略低，但db24的p值更高，说明经过其降噪，保留更多能量;e值较低，说明降噪后信号相似度比sym9高。

综合比较，所选的小波基db24优于其他小波基，是最优小波基。

表3 使用不同小波基对实验信号降噪指标计算结果

对使用db24小波降噪后的故障实验信号做Hilbert包络解调分析，得解调谱图如图11所示。

从图中可以看出在76．88 Hz处出现峰值，以后出现峰值都是该频率的倍频，76．88恰好是外圈故障特征频率，与预想相符，说明本方法是有效的。因此，可以诊断，出现故障为外圈故障。

5 结语

本文基于SUMVAR值计算结果进行最优小波基的选取，即使用不同的母小波分别计算其小波系数最大方差和即SUMVAR值，最后得到最大SUMVAR的小波为db24。用该小波及db15，sym14分别对轴承仿真信号进行降噪处理，分析降噪后信号 p，e，Kv等指标，验证了db24小波较其他小波的优越性。用db24及db20，sym9小波分别对故障实验信号进行降噪处理，同样分析降噪后信号p，e，Kv等指标，再次显示了db24小波的优越性。综合研究结果，表明所选小波基db24是最优小波基。

参考文献

［1］王丽，于宗艳．小波分析在滚动轴承故障诊断中的应用［J］．现代科学仪器，2009，12（6）:63 －65．

［2］王楠，孙凤久，陈长征．基于小波分析的低速重载轴承故障诊断［J］．东北大学学报，2005，26（1）:281 －283．

［3］程军圣，于德介，邓乾旺，等．连续小波变换在滚动轴承故障诊断中的应用［J］．中国机械工程，2003，14（23）:2037 －2040．

［4］RAFIEE J，TSE P W．Use of autocorrelation of wavelet coefficients for fault diagnosis［J］．Mechanical Systems and Signal，2009，2（8）:1 － 29．

［5］寿海飞，曹志锡，楼建勇．基于小波变换的齿轮振动信号降噪分析［J］．机械设计与制造，2007，10:125 －126．

［6］张德丰．MATLAB小波分析［M］．北京:机械工业出版社，2008:50－51．

［7］丁康，李巍华，朱小勇．齿轮及齿轮箱故障诊断实用技术［M］．北京:机械工业出版社，2005．