基于牛顿迭代搜索法的多节点协同振源定位研究*

朱亚坤，冯立杰

(1.武警工程学院研究生管理大队，西安 710086;2.武警工程学院通信工程系，西安 710086)

多节点协同振源定位技术无论是在桥梁监控、仓库监视、环境监测，还是在军事上对哨位监视、战场探测等方面有着广泛的应用。近年来，由于时差测量技术和精度的不断提高，基于到达时间差(Time difference of arrival，TDOA)的目标定位技术成为该领域的热点之一，产生了丰富多样的定位算法。受应用环境和系统复杂度等因素的影响，采用多节点协同定位对二维空间的目标进行定位更为适宜，如人迹罕至恶劣条件的边远地区边境巡逻的被动定位等。目前研究较多的是特殊平面阵列(如十字阵、五元阵)的目标定位技术［1］，本文对传感器阵列的牛顿迭代协同定位进行研究。目标定位算法通过求解一组以各传感器为焦点的双曲线方程(即TDOA方程)获得目标空间坐标的估计［2］。由于TDOA估计误差无法避免，如何提高定位精度是定位技术应用的关键。本文通过引入灰色关联的概念建立了多传感器节点协同定位的模型，其次讨论了多节点协同定位的原理与算法，最后将该算法与平均加权算法［3］和最小二乘法［4］进行仿真比较。

1 灰色关联

图1 多节点协同定位模型

在多节点协同定位中(如图1)，对来自于同一目标的振源信号先进行相关分析是很重要的。实际经验已表明，对相同的振源，采集的不同的传感器节点信号在同一时间内特征参数(如频率、过零率、振幅，频谱密度等)具有很大的相似性。所以，对采集的各节点信号某些特征参数，按振源信号类内相似性尽量大、类间相似性尽量小的准则［5］加以相关处理。由于灰色关联度的基本思想是根据曲线间相似程度来判断因素间的关联程度的，这里采用灰色系统理论的绝对关联度定义和性质来实现。

假设X0=(x0(1)，x0(2)，x0(3)，…，x0(n))为参考节点的收到的振源信号特征序列(即，为要定位的振源信号特征序列，x0(k)(k=1，2，3，…，n)为该振源信号所对应的特征参数，如频率、过零率、振幅，频谱密度等)，Xi=(xi(1)，xi(2)，xi(3)，…，xi(n))，i=1，2，3，…，m为某节点协同定位的与之比较的振源信号特征序列(以上序列均归一化)，则X0与Xi的灰色绝对关联度定义为［6］:

于是 ζ0i(i=1，2，3，…，m)中的最大值所对应的信号，既是要定位的振源信号.

2 定位原理

对振源进行定位，实质上是一种无源定位技术，采用多站测向交叉的方法来实现对振源的定位［7］。振源定位系统每个接收基阵的若干个(4个以上)接收传感器阵元按某种几何关系进行布阵。由于各接收传感器无法得到信源发出信号的时刻，它们难以实现时间同步，只能利用信号到达N个接收传感器之间的时延差，建立双曲面交汇模型来求解振源位置［8］。

建立了一个以特定基点为坐标原点(0，0)的二维坐标系。设已知N个接收传感器在此坐标系中的坐标为Ci(xi，yi)(i=1，2，…N)，振源到N个接收传感器的距离值为ri(i=1，2，…N)，振源定位示意图如图2。假定振源发出信号的传播速度为常数c，τi1表示振源到第i个接收传感器与到第1个接收传感器之间的时间差，ri1表示信源到第i个接收传感器与到第1个接收传感器之间的距离差。

图2 振源定位示意图

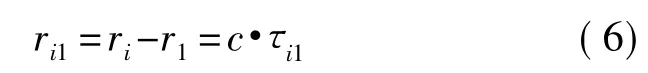
则可建立N－1个定位方程为:

求解上述方程组等价于非线性最优化问题，通过改进算法可以得到最优解。

3 定位算法

牛顿迭代法具有收敛速度快的特性，在满足一定定位精度的条件下，可以节省计算时间，但是牛顿迭代法是否收敛及其收敛速度与初始值的选择有关，解决好初始值的问题是保证牛顿迭代法良好性能的前提条件［9］。而最小二乘法具有很好的估计特性，但受测量误差的影响较大，使用最小二乘法进行定位解算会产生很大的误差，难以满足定位精度的要求。基于两种算法的优缺点，将最小二乘法的得到的估计值作为牛顿迭代算法的初始值进行迭代计算，可以很好地实现算法的优化。根据牛顿迭代搜索法的条件，从N－1个方程中选出前2个建立如下方程组:

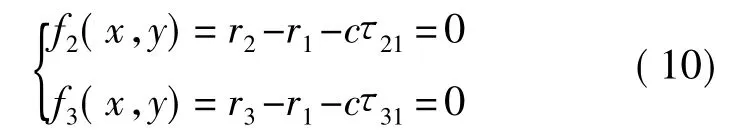
其雅可比矩阵为:

当雅可比矩阵为非奇异阵时，［f'(x，y)］－1存在，则必满足det(f')≠0，具体表示为:如果满足上述条件，则振源的位置利用牛顿迭代法可表示为［10］:

由上述表达式可知，要得到振源的精确位置，需要设定合适的初值(x(0)，y(0))，才能保证算法是否收敛及其收敛速度。

由前面的分析可知，为了解决信源初始值的选定问题，可以充分利用最小二乘法的估计结果，作为牛顿迭代法的初始值。根据文献［4］的推导结果，可以得到如下线性方程组:

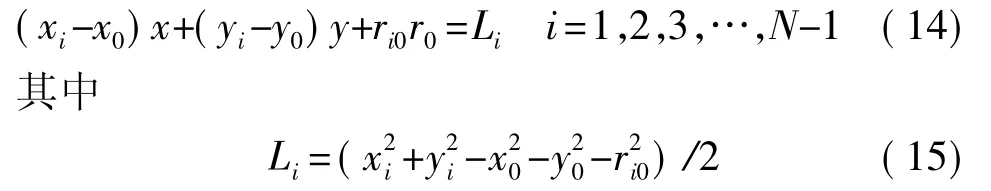
将方程组(14)转化成矩阵型式为［11］:

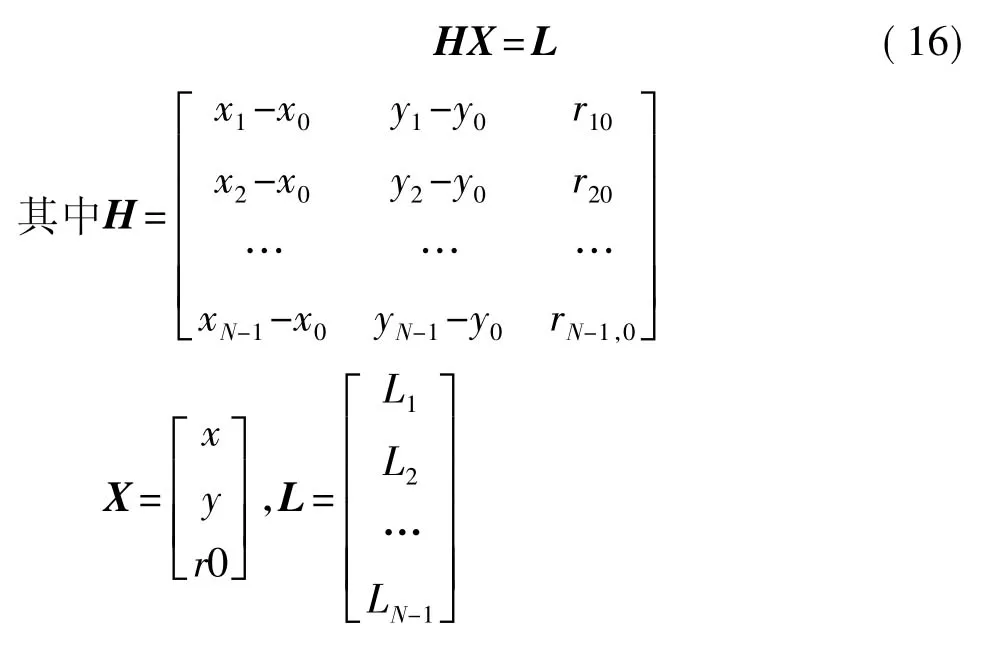
利用最小二乘法得到估计解:

4 仿真实验

为了验证改进算法的性能，对此算法与平均加权法和最小二乘法法进行了仿真，比较三者的统计特性，这里的估计器都是有偏估计器，其性能评价准则一般采用均方根误差(RMS)，即

式中:α为样本估计偏差;β为样本标准方差。本文将使用Monte-Carlo方法比较三种算法的样本偏差、样本标准方差和均方根误差。仿真中采用5个传感器组成的半径为10 m的平面圆阵，建立坐标系如图3所示。

设振动传播的速度c=140 m/s，TDOA测量值由真实的TDOA值加上零均值，方差为σrms的白噪声序列得到。这里设σrms=0.05 m，那么TDOA测量误差的方差 σrms/c为357 μs。

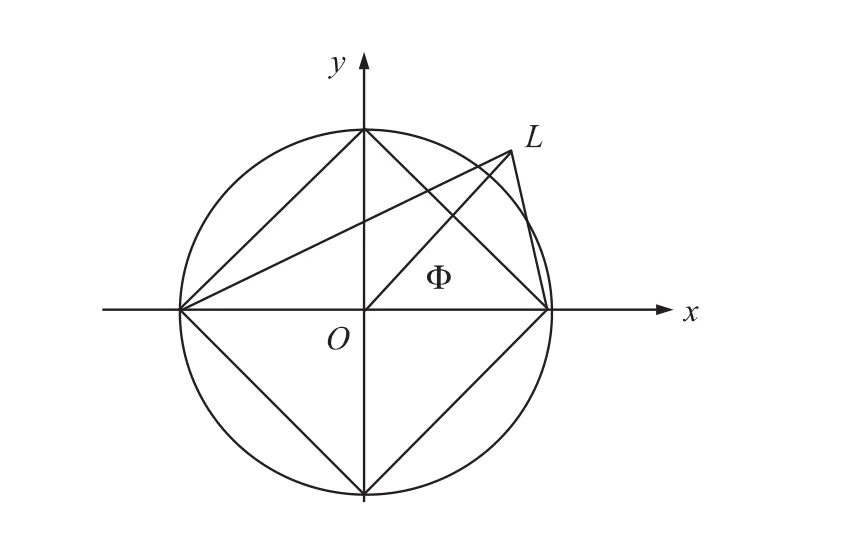
图3 五元十字阵传感器阵列和目标的关系

五元十字阵可以看作是8个等腰直角三角阵和两个线形振的组合。

对于等腰直角三角形定位算法，可知:

对于线性振定位算法，可知:

令此算法为算法1，平均加权法为算法2，最小二乘法为算法3。

目标方位角Φ=π/4，阵源L距原点的距离为r从20 m到100 m的范围变化。对近场目标，目标到原点的距离r从20 m到100 m之间变化时，定位误差曲线如图4所示。

在r=50 m时，Φ的误差如图5所示。

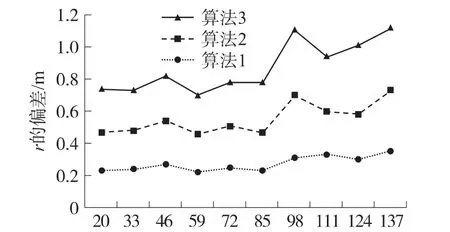
图4 偏角固定的近场目标定位误差

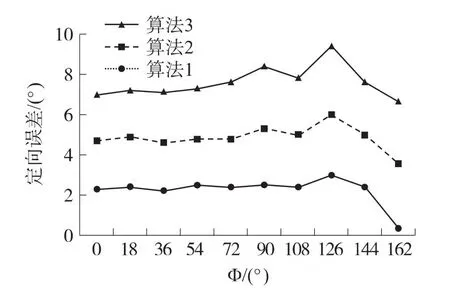
图5 距离固定的近场目标定向误差

从图4图5可以看出，对近场目标，通过算法1的样本定位精度提高了3～10倍。算法1曲线较平稳，在抑制标准方差上性能最佳，抑噪性能最优。

以目标到原点的距离大于阵列孔径10倍作为远场目标。对远场目标，设Φ=π/6，定位误差曲线如图6所示。

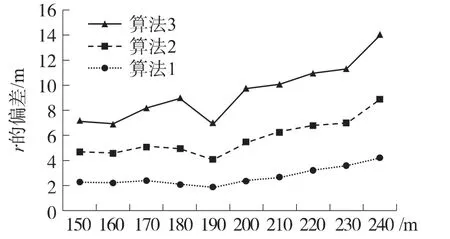
图6 偏角固定的远场目标定位误差

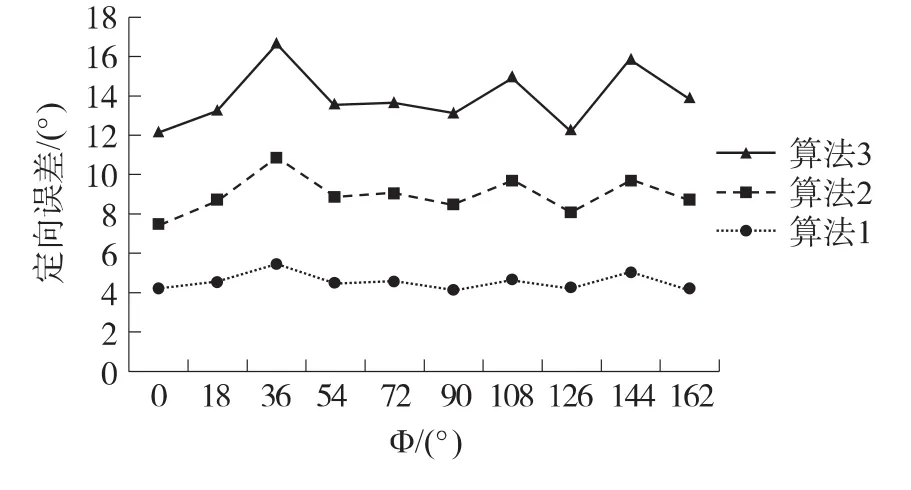
图7 距离固定的远场目标定向误差

由图6可以看出，对远场目标，各算法样本偏差差别较大。算法1在样本标准方差上性能明显优于算法2，3，从而r的均方根误差最小。此外，通过仿真也可以看出使用平面阵对目标进行定位，随着目标距离增大，目标定位误差也随之增加。

由图7可以看出，在远场目标，算法1的目标定向的精度比算法2高出近4倍，比算法3高出近10倍，在r=200时，算法1的定向误差范围是2 m，算法2的定向范围误差是4 m，算法3的定向误差范围是6 m。

5 结束语

本文解决了牛顿迭代法的初始值问题，避免了人为设定初始值造成牛顿迭代算法的不收敛，实现了算法的优化。实验结果表明，牛顿迭代定位算法具有良好的收敛性能，文中提出的算法对于提高协同定位精度是有效的。算法对近、远场目标定位性能均优于传统的最小二乘法和平均加权法，改善了TDOA测量误差对目标定位精度的影响。

［1］郅熙彪，王位策，刘强，等.正三角震动阵列对地面目标定位研究［J］.探测与控制学报，2006，08(4):27－29.

［2］SCHAU H C，ROBINSON A Z.Passive Source Location Employing Intersecting Spherical Surfaces from Time-of-Arrival Difference［J］.IEEE Transon Acoustic，Speech，and Signal Processing.1987.ASSP－35(1):1223－1225.

［3］孙勇，景博，张吉力.最优加权与递推最小二乘法相结合的多传感器信息融合［J］.传感技术学报，2004，17(12):630－632，654.

［4］刘利军，韩焱.基于最小二乘法的牛顿迭代信源定位算法［J］.导弹与制导学报，2006，26(3):325－328.

［5］Harwig D，Lin S Y.Proc 6th Int Conf Trends in Welding Reserch［R］.Material Park，OH:ASM，international，2003:995.

［6］Smith J，Abel S.Closed-Form Least-Squares Source Location Estimation from Range-Difference［J］.IEEE Trans Acoust，Speech，Signal Processing，1987，35(12):1661－1669.

［7］Friedlander B.A Passive Localization Algorithm Andits Accuracy Analysis［J］.IEEE J Ocean Eng，1987，12(1):234－245.

［8］Fang B T.Simple Solutions for Hyperbolic and Relatedposition Fixes［J］.IEEE Trans Aerosp Eletron Syst，1990，26(9):748－753.

［9］Schau H C，Robinson.Passive Source Localization Employing Intersecting Spherical Surfaces from Time-of-Arrival Differences［J］.IEEE Trans Acoust，Speech，Signal Processing，1987，35(8):1223－1225.

［10］DING F，CHEN T.Identification of Multivariable Systems Based on Finite Impulse Response Models with Flexible Orders［C］//Proceeding of the IEEE International Conference on Mechatronics＆Automation Niagara Falls.Piscataway:IEEE，2005:770－775.

［11］罗庆生，韩宝玲.一种基于超声波与红外线探测技术的测距定位系统［J］.计算机测量与控制，2005，13(4):304－306.