基于光电扫描的网络式大尺寸测量系统定位算法研究*

端木琼，杨学友，邾继贵，杨淩辉，劳达宝

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

大尺寸精密测量技术是重大装备如大型飞机制造、数字化造船、大型机电设备安装等制造过程中的支撑技术之一，是保证质量的关键［1］。在大尺寸测量的过程中，测量范围与测量精度矛盾突出，传统的测量手段难以满足工业上对测量范围和测量精度的双重需求［2］。目前，常用的大尺寸测量设备主要有激光跟踪仪、电子经纬仪和摄影测量系统［3］。这些测量系统在使用中都曝露出各自的缺陷，如激光跟踪仪测量系统每次只能跟踪测量一个目标，经纬仪系统需要逐点手工测量，为了适应大型设备安装的需求，人们提出了网络式测量系统。网络式测量系统由多个测量基站组成，具有实时性好、抗干扰能力强、易于扩展的特点，通过增加测量基站数量，将测量空间划分成若干个子测量空间，协调测量精度与测量范围的矛盾，实现大空间范围内的高精度测量。

天津大学精密测试技术及仪器国家重点实验室在研究了常用的大尺寸测量系统的基础上，结合Metris公司推出的iGPS测量系统，设计出了一套基于光电扫描的网络式大尺寸测量系统，称之为wMPS(workspace Measuring Position System)。该系统以电子经纬仪的交会式测量原理为基础，引入了光电扫描的角度测量方法，提高了系统的自动化程度和并行测量能力，非常适合工业现场大尺寸测量与质量控制。文献［4］研究了wMPS系统的组成以及系统结构，建立了发射器模型，提出了基于角度交会的坐标计算方法，并通过实验进行了验证，文献［2］对系统的内参数标定以及系统定向方法进行了研究，提出了系统内外参数的标定方法。文献［5］在角度交会测量方法的基础上提出了利用平面交会计算坐标的新方法。本文在此基础上对角度交会方法和平面交会方法进行了证明和比较，分析了主要误差，并通过实验平台对这两种算法进行了比较、验证。实验证明，利用基于光平面交会的算法能够极大的改善系统精度，可满足大多数工业及军工现场使用的要求，应用前景广泛。

1 wMPS硬件系统组成及原理

wMPS三维测量系统主要由激光发射器网络、位置传感器、中心计算机和无线通讯系统组成，如图1所示［4－7］。激光发射器由固定基座和转动头组成，安装有两个一字线激光器和一个脉冲激光器，两个一字线激光器固定于转动头上，激光器产生的光平面分别与垂直方向呈±30°，呈V字形。当发射器工作时，激光器所产生的光平面随转动头一同旋转，对测量空间进行扫描。脉冲激光器用于产生一个计时同步时刻，以该时刻光平面1与发射器水平面之间的交线为发射器X正方向，旋转轴为Z方向，按右手定则确定Y方向。发射器产生的光信号由位置传感器接收，从而计算得到发射器的方位角(水平方位角和垂直方位角)，通过同步计算传感器与多个发射器之间的方位角进行交会获得传感器的三维坐标。由于反射器和接收器之间的光信号是单向传输，因此多个位置传感器可以同时利用这些光信号同时工作。

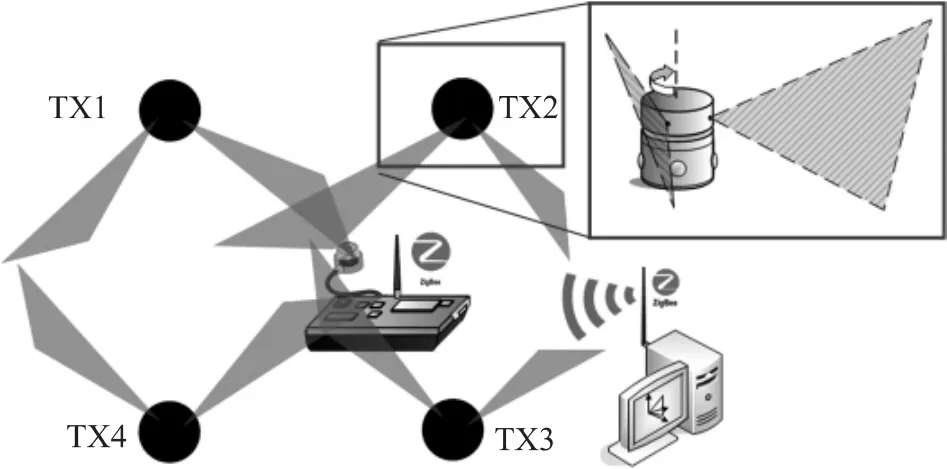
图1 wMPS测量系统组成

2 基于角度交会的定位方法

2.1 wMPS角度测量原理

发射器可以抽象为围绕旋转轴以角速度ω旋转的两个光平面［4－5］。发射器的扇形光平面与旋转轴的夹角为±γ，两扇形光面在发射器水平面交线夹角为θoff，设从计时同步时刻到发射器第一个光平面扫过位置传感器的时间间隔为t1，两个光平面扫过位置传感器的时间间隔为t2，则位置传感器相对于发射器原点的水平角α和垂直角β可以通过方程1求得［6－7］:

2.2 角度交会定位算法

由于wMPS系统测量得到的是传感器与发射器之间方位角信息，因此对于某个接收器，能同时接收到两个或两个以上的发射器发射的信号，就可以确定位置传感器的空间位置坐标，下面以包含两个发射器的最小系统推导wMPS测量系统的角度交会定位原理［8－10］。

如图2所示，假定两个发射器分别位于O'点和O点，发射器A的坐标系为OXYZ，发射器B的坐标系为O'X'Y'Z'，被测点P在OXYZ下的坐标为(u，v，w)，在O'X'Y'Z'下的坐标为(u'，v'，w')。坐标系O'X'Y'Z'相对于OXYZ的坐标转换旋转矩阵和平移矩阵分别为R和T，。(θ，φ)和(θ'，φ')分别为被测点P与发射器A、发射器B的水平角和垂直角。向量可以表示为:

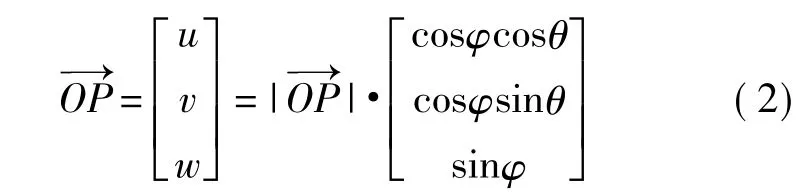
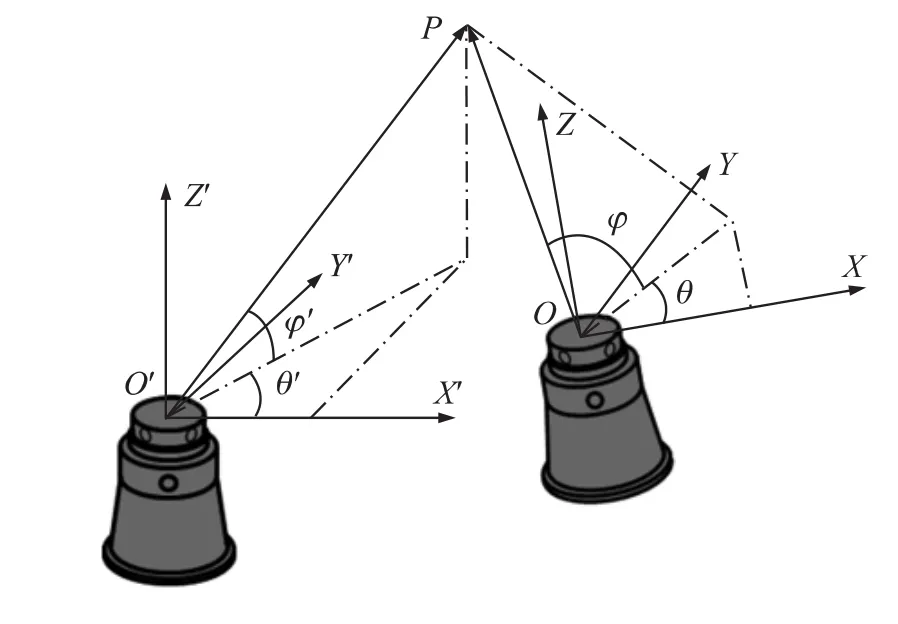
图2 基于两个发射器的角度交会定位原理

将向量单位化并将其水平角θ和垂直角φ分别旋转π/2可以得到两个与垂直的向量a和 b［11－12］。

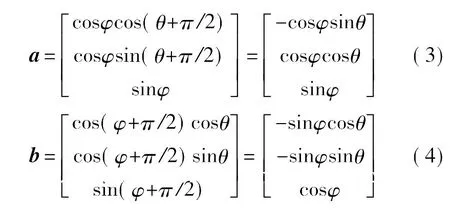
由垂直关系可以得到

与之类似，对发射器2可得到

方程(5)、(6)可以得到方程组(7)。

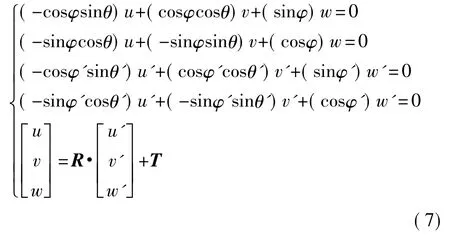
通过解方程组(7)可以得到被测点P在全局坐标系OXYZ下的坐标(u，v，w)，当发射器多余两个时，可以列出多个方程，用最小二乘法求最优解。

2.3 角度交会测量误差分析

角度交会测量方法计算坐标的误差主要来自于方位角测量误差。在上文对测量算法的推导中，假定两个光平面交于旋转轴上同一点O，但实际上由于制造技术限制，发射站的两个扫描光平面不会严格与转轴交汇于发射站原点O，而是与转轴相交于两个不同位置:O、O'，即两个光平面虽然绕同一转轴旋转但旋转中心不同，如图3所示。此时，光平面2与旋转轴的交点O'到原点O的距离为Δz。如图4所示，当平面2扫过被测点P时，由几何关系可得:

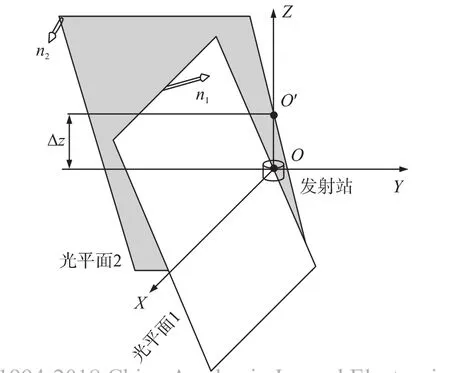
图3 两光平面不交于轴上同一点发射器模型

式(8)表明，水平角和垂直角的测量误差不仅与Δz有关，还与被测点与发射器的水平距离l和垂直高度h有关，以及，因此该误差难以补偿。当水平面的倾角 γ 为－45°，Δz为 0.1 mm，工作距离为 5 m 时，水平角的误差小于2″，垂直角误差小于6″。

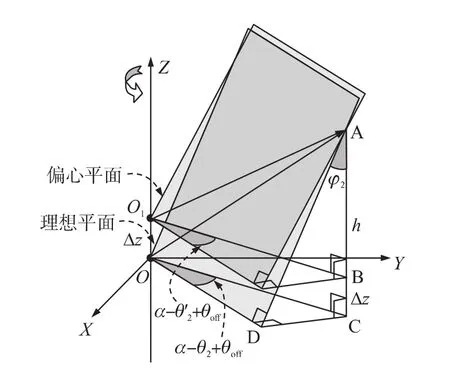
图4 两平面不交于轴上同一点测量误差

3 基于光平面交会的测量方法

3.1 平面交会定位算法

仍然以包含两个发射器的系统推导wMPS测量系统的光平面交会定位算法［4］。发射器的坐标系、被测点的坐标以及坐标系转换的旋转矩阵和平移矩阵与上文定义相同。对于一个发射器，在测量前预先标定出两个扇形光平面的法向量n1(t0)和n2(t0)。

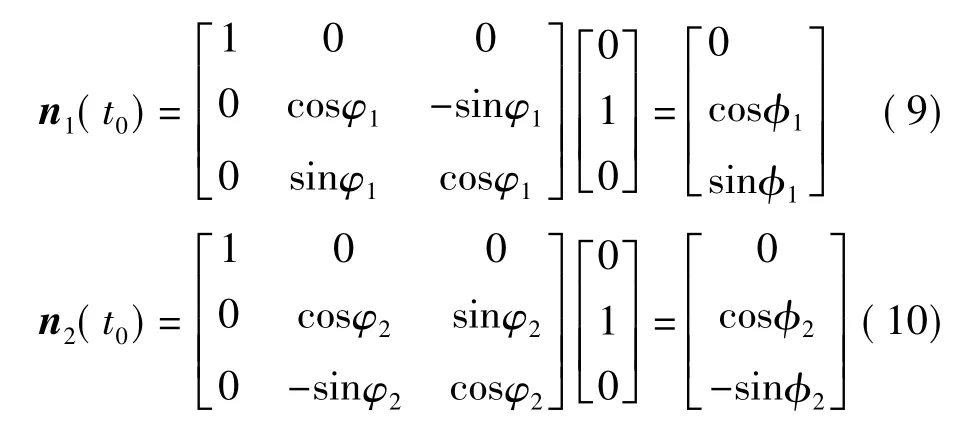
假设发射器在t0时刻开始工作，以角速度ω绕Z轴旋转，在t1时刻光平面1经过被测点P，在t2时刻光平面2经过同一被测点。光平面1在t1时刻的法向量n1(t1)和光平面2在t2时刻的法向量n2(t2)分别为

其中，θ1=ω(t1－t0)， θ2=ω(t2－t1)－θoff，θoff为光平面1与光平面2在水平面内的偏移角。在t1时刻，被测点P位于光平面1内，因此发射器原点到点P的向量与n(t)垂直，同样在t时刻，向量112与n(t)垂直。因此对于发射器A、B可得方程22组(13)

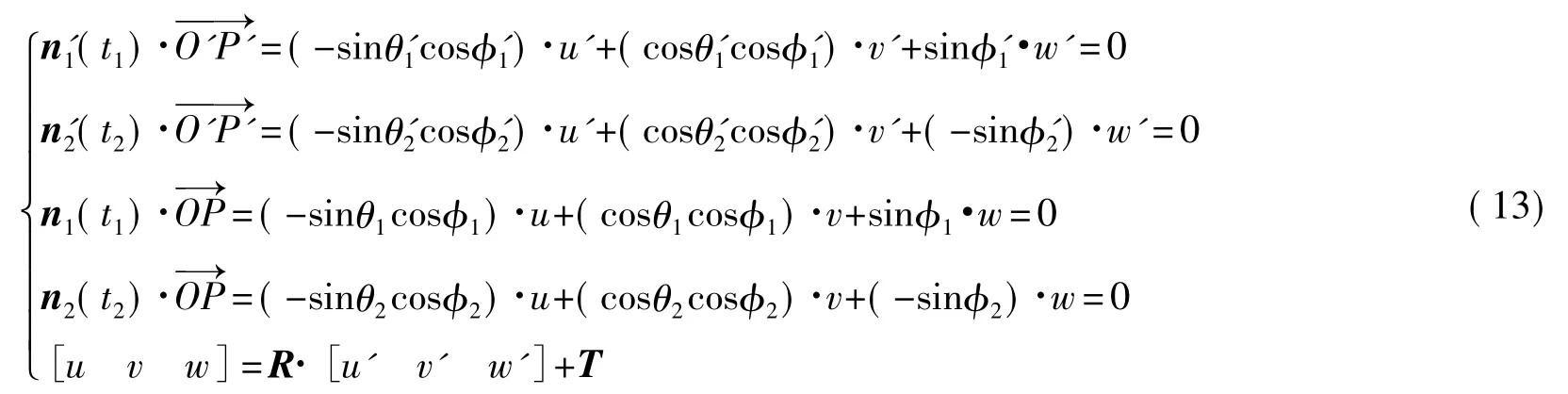
通过解方程组(13)可以得到被测点P在全局坐标系OXYZ下的坐标(u，v，w)当发射器多余两个时，用最小二乘法求最优解。

3.2 平面交会误差分析

平面交会测量的误差主要来自于发射站的模型误差。当发射站的两个扫描光平面与转轴相交于两个不同位置:O、O'，即两个光平面虽然绕同一转轴旋转但旋转中心不同，如图3所示。此时，光平面2与旋转轴的交点O'到原点O的距离为Δz，因此平面2的扫描角为θ2'=θ2+Δθ2，如图4所示。由几何关系可得:

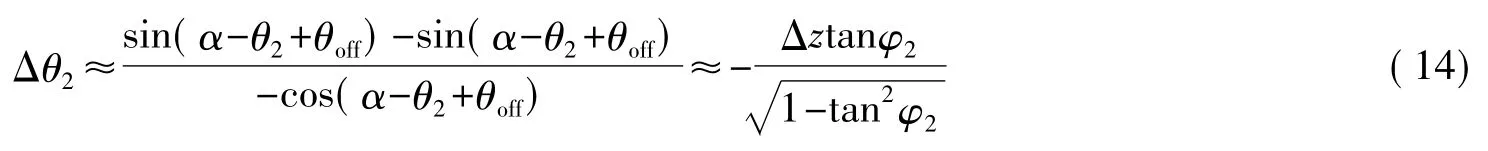
由式(13)可知，平面2扫描角的误差仅受Δz影响，在与角度交会测量同样的条件下，平面2的扫描角度误差小于4″。基于平面交会原理的交会误差主要由发射器的装配误差造成，而与测量点所在的位置无关，因此可以通过发射器内参数标定阶段测量出Δz计算出系统误差Δθ2对测量结果进行补偿。

4 实验与验证

为了验证算法的性能，采用两台发射器和一个位置传感器组成一个wMPS最小系统验证平台，在wMPS系统测量的同时，利用激光跟踪仪进行同步测量，对测量结果进行比较，如图5所示。在系统标定完成后，通过三维微移平台将位置传感器分别沿X、Y、Z方向移动，移动步长为50 mm，角度交会算法的结果如表1，平面交会算法的结果如表2所示。

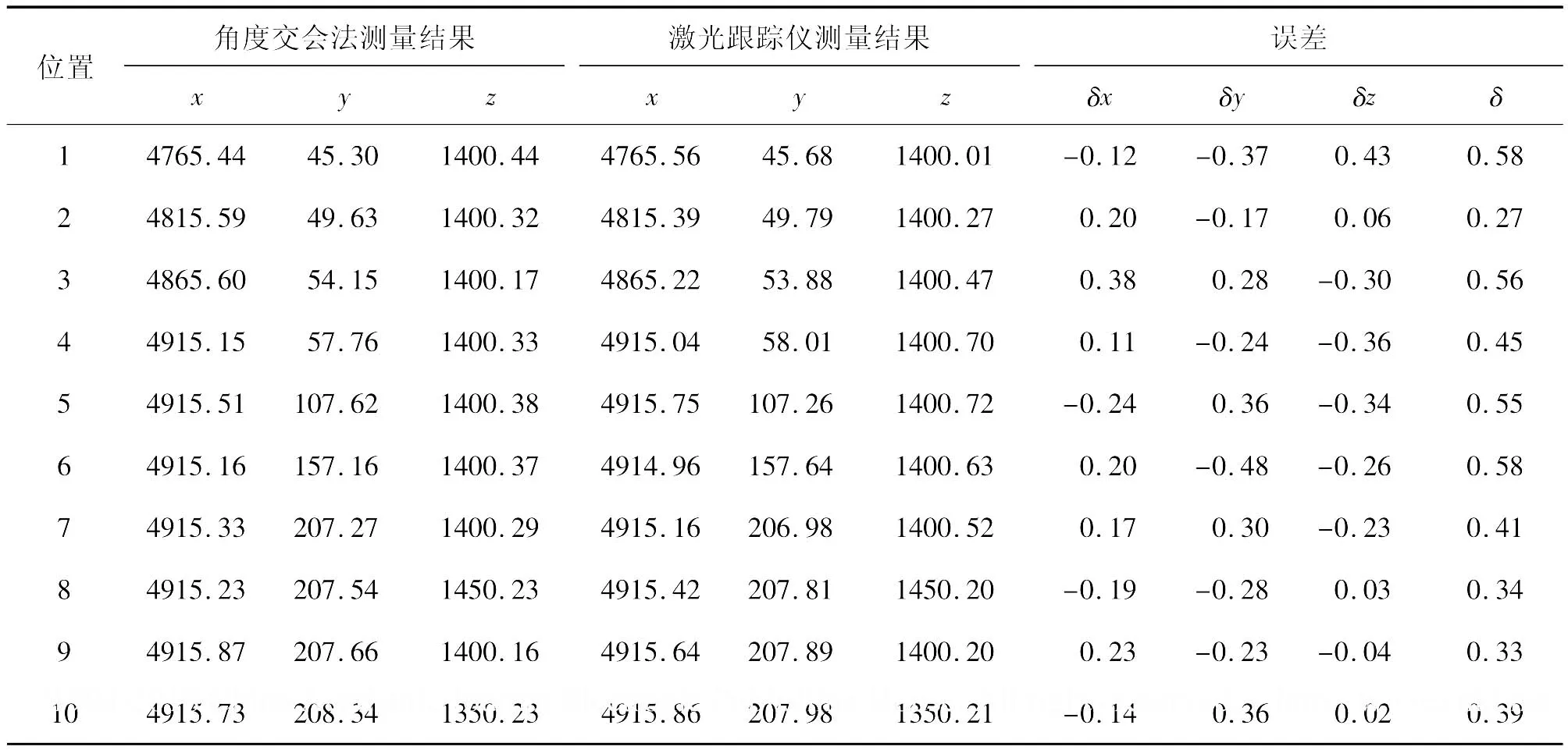
表1 角度交会法测量结果比较 mm

表2 平面交会法测量结果比较 mm

图5 wMPS系统验证平台

5 结论

本文分析证明了角度交会测量方法和平面交会测量方法，分析了光平面不交于轴上一点所带来的误差。由于该误差在角度交会测量方法中不仅与与Δz有关，还与被测点位置有关，因此难以补偿。而基于平面的交会方法中，测量误差仅与Δz有关，易于补偿。通过实验验证，结果表明，测量误差小于0.15 mm，满足大多数现场大尺寸测量需求。

［1］叶声华，邾继贵，张滋黎，等.大空间坐标尺寸测量研究的现状与发展［J］.计量学报，2008，29(z1):1－6.

［2］劳达宝，杨学友，邾继贵，等.网络式激光扫描空间定位系统标定技术研究［EB/OL］.http://www.cjmenet.com.cn/xuebaochinese/papers/allpaper/newaccepted/fulltext/2010－130.pdf，2011－03－17.

［3］黄桂平，钦桂勤.大尺寸三坐标测量方法与系统［J］.宇航计测技术，2007，27(04):15－19.

［4］YANG Linghui，YANG Xueyou，ZHU Jigui，et al，Novel Method for Spatial Angle Measurement Based on Rotating Planar Laser Beams［J］.Chinese Journal of Mechanical Engineering，2010，23(6):758－764.

［5］杨凌辉，杨学友，劳达宝，等.采用光平面交汇的大尺寸坐标测量方法［J］.红外与激光工程，2010，39(6):1105－1109.

［6］Arcsecond Inc.Workspace Advanced Metrology Edition User’s Guide.2003.

［7］闫奇瑾.基于室内GPS的弹头形心轴线测量方法的研究［D］.哈尔滨:哈尔滨工业大学，2007.

［8］李广云.非正交系坐标测量系统原理及进展［J］.测绘信息与工程，2003，28(1):4－10.

［9］邾继贵，王鑫，王大为，等.光学坐标测量系统技术研究［J］.传感技术学报，2007，20(4):778－780.

［10］张滋黎，邾继贵，耿娜，等.双经纬仪三维坐标测量系统设计［J］.传感技术学报，2010，23(5):660－664.

［11］Kutluyil Dogancay，Gokhan Ibal.3D Passive Localization in the Presence of Large Bearing Noise［EB/OL］.http://www.eurasip.org/Proceedings/Eusipco/Eusipco2005/defevent/papers/cr1189.pdf，2011－03－17.

［12］D A Maisano，J Jamshidi，F Franceschini，et al.A Comparison of Two Distributed Large-Volume Measurement Systems:The Mobile Spatial Coordinate Measuring System and the Indoor Global Positioning System［J］.Proceedings of the Institution of Mechanical Engineers，2009，223(n5):511－521.