紧耦合MINS/GPS组合导航系统数据融合的分析与处理

马 骏，杨功流

(1.天津大学机械工程学院，天津 300072;2.北京航空航天大学仪器科学与光电学院，北京 100191)

微惯性测量单元(MIMU)和卫星导航系统(GPS)构成的MINS/GPS组合导航系统，成本低、体积小、重量轻、功耗小、具有很高的综合性能优势，在民用测量、汽车控制与导航制导等领域得到越来越多的应用。从公开报道的文献看，采用微机械陀螺和微机械加速度计能进一步降低MIMU的成本，并且使其体积、重量和功耗也更小，使得采用微机械技术实现中低精度惯导系统的成本大大降低。同时，通过与卫星导航系统如GPS、GLILEO、GLONASS的组合降低对捷联惯导系统的要求。如何更好的发挥INS/GPS组合导航系统的性能，国外在1990年左右开始了紧耦合INS/GPS 组合试验研究，1997 年开始实际应用［1－2］。而我国随着北斗导航系统(BD)的部署的逐步深入，在发展基于我国北斗系统的紧耦合INS/BD组合系统时，有必要多角度的考虑GPS的耦合机理，为我国的卫星组合导航系统提供理论参考。

1 MINS/GPS组合导航系统特性

在GPS与惯导系统的组合方式中，按照信息交换或组合程度的不同，GPS和惯导的组合方式一般分为三种方式:松耦合、紧耦合、超紧耦合。在松耦合系统中，惯导系统和GPS接收机各自独立工作，在GPS接收机可工作时，由融合算法使惯性导航系统的输出调整到GPS的位置和速度上，并用最优估计结果反馈修正惯导系统或直接修正惯导输出，系统工作原理如图1所示［3］。

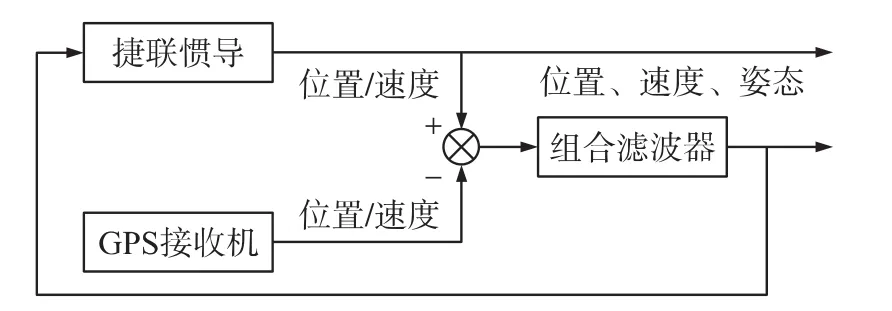
图1 松耦合MINS/GPS组合方框图

在GPS接收机不可工作时，惯导系统独立工作;紧耦合系统中，GPS接收机提供伪距、载波相位和多普勒频移信息与惯导系统的数据集中在一个滤波器中处理，误差状态包含了惯导系统的导航解算误差和GPS接收机误差，采用卡尔曼滤波器提供最佳的导航结算结果，同时还用于辅助GPS码环锁相过程，系统工作如图 2 所示［1，4］。

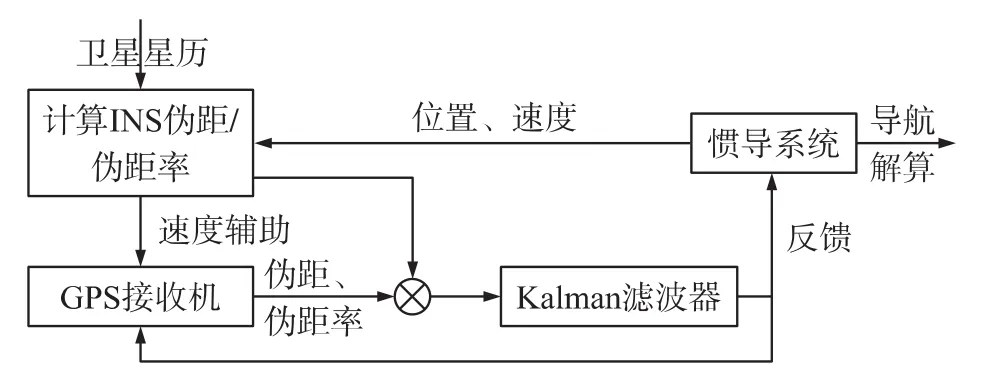
图2 紧耦合MINS/GPS组合方框图

超紧耦合系统除了具有松耦合和紧耦合系统所具有的优点外，在结构上，组合发生在跟踪回路中，直接利用IMU量测信息辅助GPS码跟踪环和载波跟踪环，并且在MINS/GPS组合系统通过一个组合卡尔曼滤波器反馈回路代替传统的跟踪环回路，系统工作原理如图3所示［1］。

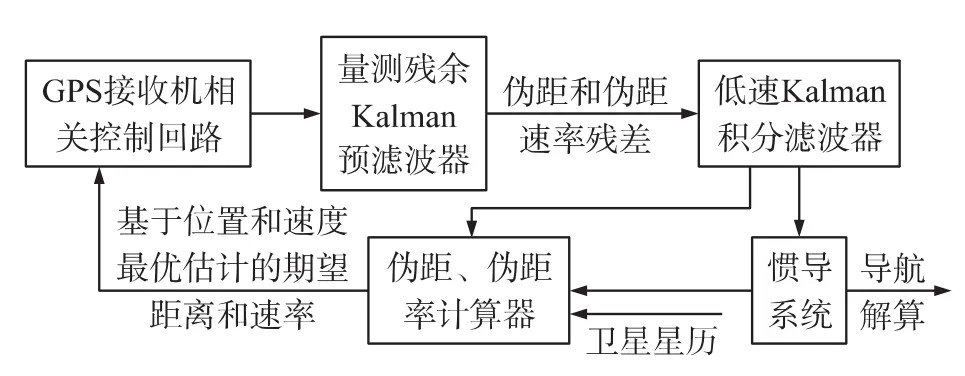
图3 超紧耦合MINS/GPS组合方框图

在紧耦合组合系统中，不涉及GPS接收机内部的编排，主要问题集中在卡尔曼滤波器数据优化处理的方式方法上，在实现系统的最优组合时会遇到所谓的“维数灾难”。因此，在研究组合数据处理时，注重研究分散化滤波算法，通过对信息融合不同算法的仿真，寻求系统最佳的信息融合。超紧耦合虽然有无可比拟的优点，但是涉及到GPS接收机内部编排，实施难度较大，国内研究受限于接收机研制能力，在超紧耦合MINS/GPS组合研究方面基本上都停留在仿真设计阶段，并没有得到物理工程试验，距离实际工程应用距离较大［1，5］。

2 紧耦合组合系统滤波算法

对GPS和惯导数据进行处理时，需要综合考虑所有可能得到的传感器信息，以期得到一个位置、速度和姿态等最佳估计。在数据处理中最常用的算法工具是卡尔曼滤波器，卡尔曼滤波器用于实时融合动态冗余多传感器数据，在测量模型统计特性已知的情况下能够递推得到统计意义下最优的融合数据估计。当 GPS中可见星数大于4颗时，松耦合MINS/GPS组合系统的位置/速度组合的卡尔曼滤波器设计已广泛运用于各型成熟系统中［6］，文中仅给出紧耦合MINS/GPS组合系统在基于~G矩阵选星算法［3，7］的伪距、伪距率的状态方程和量测方程。

2.1 伪距/伪距率组合的MINS/GPS紧耦合系统状态方程

MINS的误差状态为速度误差、姿态误差、位置误差、陀螺漂移、加速度计零偏;GPS的误差状态，紧耦合状态矩阵F参考捷联式松耦合的状态矩阵的选取原则，在此基础上添加了伪距、伪距率组合系统中相关的误差变量，通常取两个与时间有关的误差［7－10］:一个是与时钟误差等效的距离误差 δtu，另一个是与时钟频率误差等效的距离变化率误差δtru。组合系统状态方程为

其中，

其中G(t)为17×8维系统噪声驱动矩阵，W(t)为8×1维系统激励噪声向量。

2.2 伪距/伪距率组合的MINS/GPS紧耦合系统量测方程

在紧耦合组合系统中，设地心地球固连坐标系中MINS相对于第i颗卫星的伪距记为，同时设GPS接收机测量得到的第i颗卫星的伪距记为，惯导位置误差在地心地球固连坐标系中坐标为(δx，δy，δz)，则 MINS 和 GPS 的伪距差［11－12］可表示为:

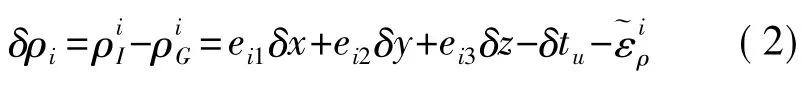
令伪距差量测误差为:

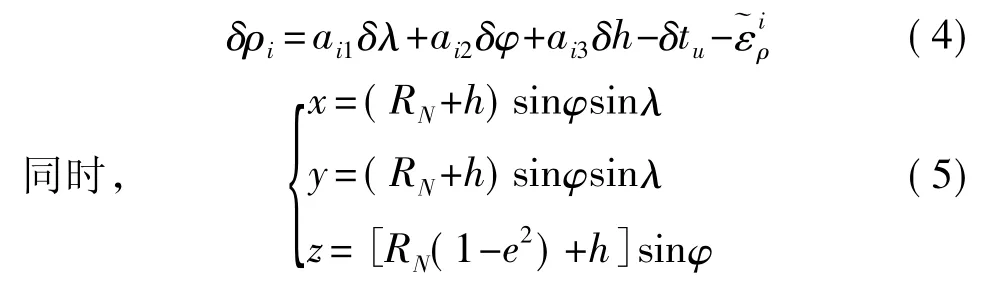
于是有

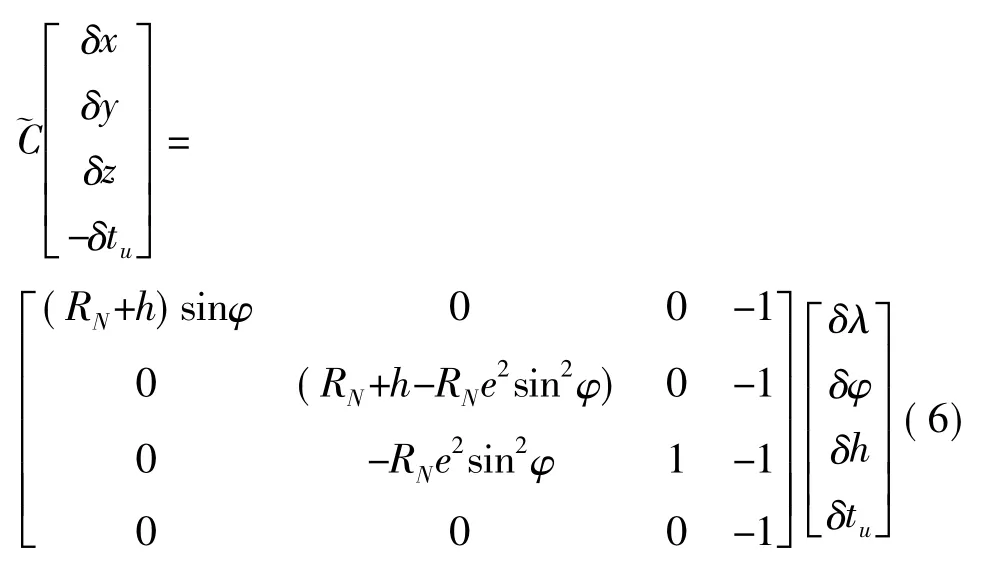
其中令

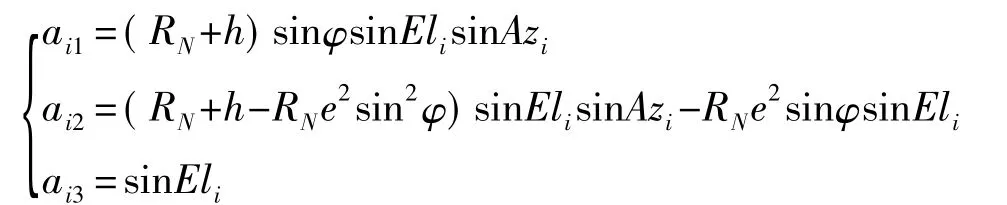
由此可得

可得伪距量测方程

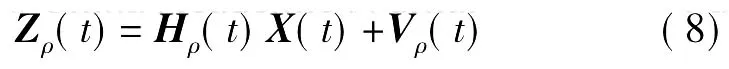
式中，Hρ=［04×304×3Hρ104×304×3Hρ2］4×17

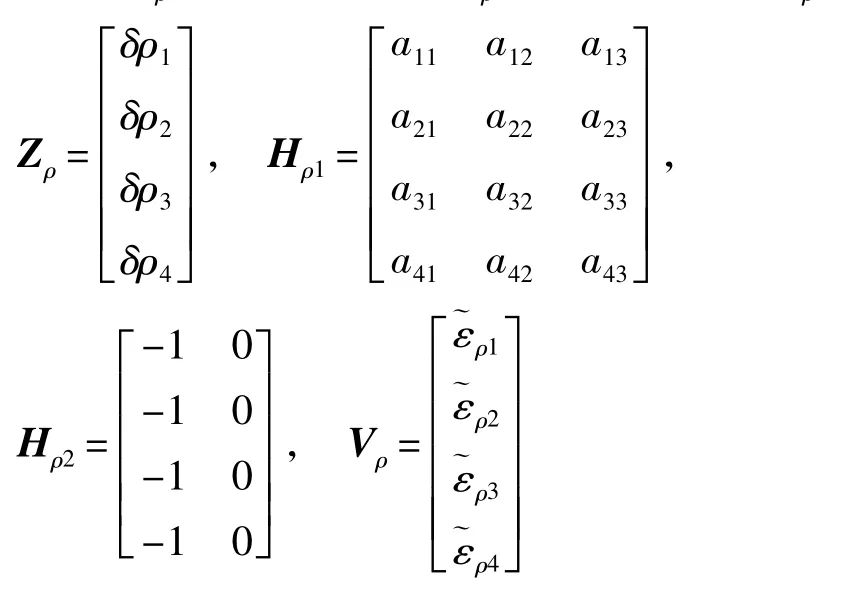
同理可推得伪距率之差的量测方程为:

其中，bi1=sinElisinAzi，bi2=sinElisinAzi，bi3=sinEli，为伪距率残留误差。由此可得

于是得到伪距量测方程

由式(8)、(11)可得到基于伪距、伪距率的MINS/GPS组合系统的量测方程

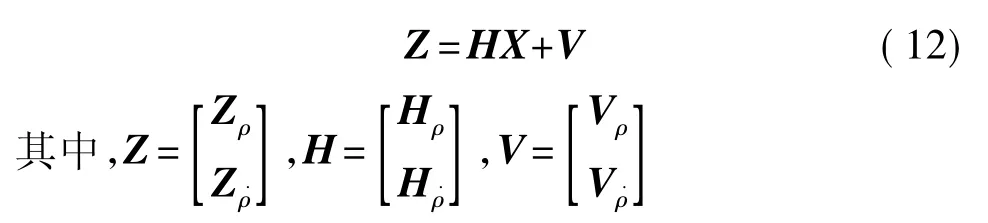
3 试验结果与分析

本文通过静态试验对以上组合算法有效性进行验证。为了便于分析，在试验中记录了导航器件的原始数据，利用半实物仿真的方法进行不同组合算法的导航解算，从而更加确定组合算法间的性能差异。在试验中，陀螺仪和加速度计的短期精度约为0.06°/h 和10－4gn，GPS 接收机采用加拿大 NovAtel公司的DL－V3，可输出位置、速度、航迹角、伪距、伪距率以及卫星星历。静态试验在某高层楼顶进行，周围无遮挡，可见星为10～11颗。在这种情况下对比了松耦合和紧耦合的位置、速度、航向误差。

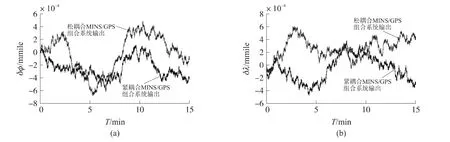
图4 位置误差的对比

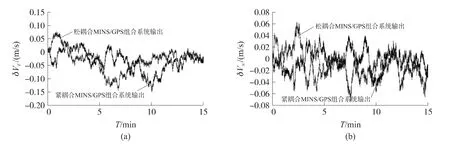
图5 速度误差对比

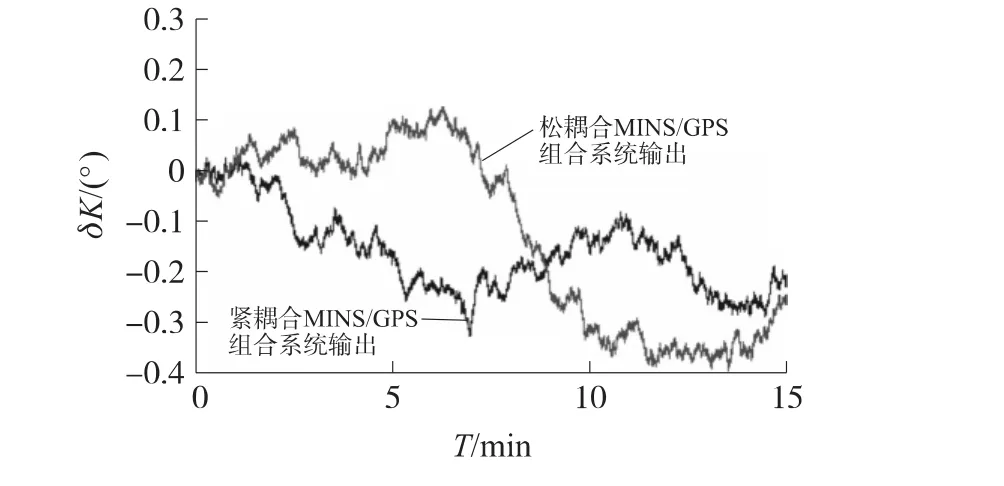
图6 航向角误差对比

从以上试验可以看到，在可见卫星大于4颗时，松耦合和紧耦合的组合方式在位置、速度、航向上没有明显差别。将采集到的GPS信息进行处理，0～5 s为6颗可见卫星，5 s～10 s为3颗可见卫星，10 s～15 s又恢复6颗可见星。半实物仿真试验如图7～图11所示。

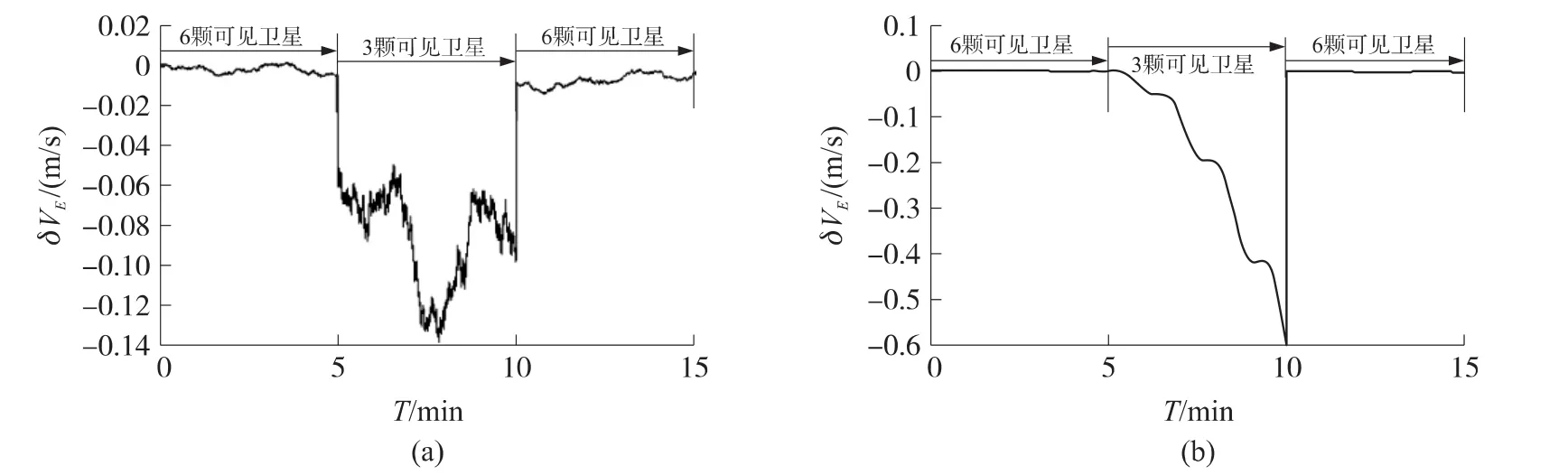
图7 可见卫星变化时东向速度误差对比

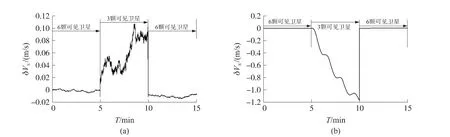
图8 可见卫星变化时北向速度误差对比

图9 可见卫星变化时纬度误差对比

图10 可见卫星变化时经度误差对比

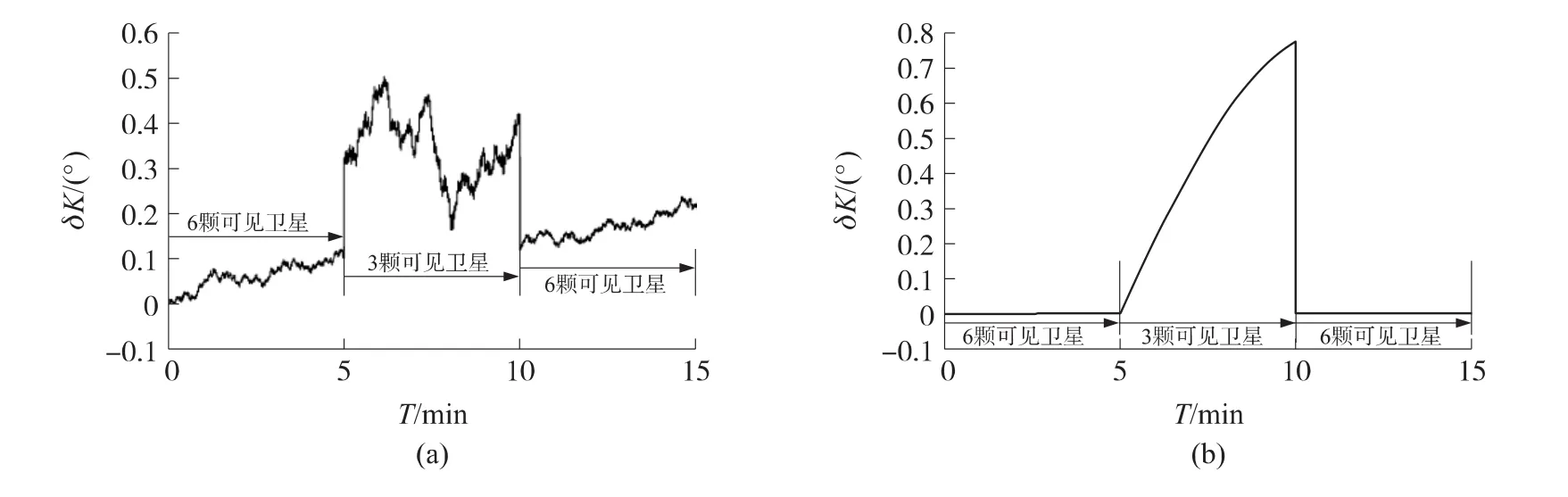
图11 可见卫星变化时航向误差对比

从图7～图11中可以看到:在紧组合方式中，可见卫星突然减为3颗时，可观测度降低，组合滤波输出产生了一个阶跃反应，但是滤波过程并没有明显发散的趋势，在紧耦合系统中，由于可见星的数量突然减少或者当换星时，伪距差会发生突跳，无法采用伪距率作为系统的量测信息，为此需要在程序中加入伪距突变的判断，当检测到伪距突跳时，只用伪距量测信息对系统进行修正;在松组合方式中，可见星少于4颗时，组合方式立即失效，导航系统的输出开始发散。

4 结论

本文对MINS/GPS组合算法进行了理论分析和建模，并用半实物仿真试验对算法的有效性进行了验证，对实际的组合效果进行了对比分析。试验结果表明，由于紧组合方式中采用了伪距、伪距率的组合算法，组合滤波量测值精度高，滤波效果好。但同

时应注意到在动态的跑车情况下，采用高动态的GPS接收机，提高修正频率，组合效果会更优，但是应考虑对于低成本的MINS/GPS组合是否合适，同时考虑到缺少伪距误差的精确建模，紧耦合系统不一定能达到理想中的组合效果，在GPS搜星突然变化时，应考虑仅采用伪距作为量测信息以减少组合系统的导航误差。因此，在研究组合数据处理的同时，还应开展对组合导航系统抗干扰能力方面的深入研究。

［1］周坤芳，吴唏，孔键.紧耦合GPS/INS组合特性及其关键技术［J］.中国惯性技术学报，2009，17(1):42－45.

［2］袁社旺，卓宁.GPS中一种选星方法及实验分析［J］.中国惯性技术学报，2008，16(4):445－447.

［3］黄昆，胡小毛，李士心.MINS/GPS组合导航系统选星算法［J］.中国惯性技术学报，2009，17(6):718－722.

［4］陈思，王可东.惯性导航与卫星导航紧耦合技术发展［J］.全球定位系统，2007(3):21－25.

［5］周星伶.GPS/INS组合导航系统松、紧耦合性能比较［J］.航空电子技术，2007(4):1－6.

［6］Skaloud J，Viret P.GPS/INS Integration［J］.European Journal of Navigation，2004，2(4):40－44.

［7］马云峰.MSINS/GPS组合导航系统及其数据融合技术研究［D］.南京.东南大学博士学位论文.2006.

［8］李倩，战兴群，王立端，等.GPS/INS组合导航系统时间同步系统设计［J］.传感技术学报，2009，22(12):18－21.

［9］LIU Guang-fu，ZHANG Wei-gong，LIU Xu，et al.Data Synchronization in IMU/GPS Integrated Measurement System of Vehicle Motion Parameters［J］.Journal of Southeast University(English E-dition)，2006，22(2):200－203.

［10］孔星炜，郭美凤，马芮，等.一种制导炸弹MINS/GPS导航系统误差分析与分配［J］.中国惯性技术学报，2009，17(1):37－41.

［11］方靖，顾启泰，刘学斌，等.MINS/GPS组合导航系统设计与实验［J］.清华大学学报(自然科学版)，2007，47(8):1316－1319.

［12］马建仓，陈静.MEMS SINS-GPS组合导航系统设计［J］.传感技术学报，2009，22(10):29－31.