埋入混凝土中压电陶瓷圆片声指向性和能量研究*

黄 润，陈 雨，李鹏程，谭 斌，陈 浩

(1.重庆大学光电工程学院光电技术及系统教育部重点实验室，重庆 400044 2.四川大学电子信息学院，成都 610065)

超声检测是混凝土结构健康检测的主要方法。传统的混凝土结构健康状态超声检测方法是在现场检测时将超声换能器安装在待检测混凝土结构上，激励换能器使其向混凝土中发射超声波，接收并分析从混凝土中反馈的超声波来判断混凝土结构的健康状态［1］，这种方法只是定期地对混凝土结构健康状态进行抽样检查，当混凝土结构出现健康问题时得不到及时的响应。因此，混凝土结构健康状态的在线监测成为国内外学者关注的焦点。美国休斯顿大学Song G等人将压电传感器埋入混凝土结构中检测其凝固早期的强度［2］;在20世纪90年代，重庆大学文玉梅等人提出了将压电陶瓷元件埋入混凝土结构中构成压电机敏模块实时在线监测混凝土结构健康状态的方法［3］;重庆大学陈雨等人在此基础上实现了混凝土结构温度和混凝土结构变化(如松动)引起的应力改变的在线监测［4－5］，但这种方法只是通过埋入混凝土中压电陶瓷各种特性参数(如耗散因子)被动地响应混凝土结构和温度变化实现的检测，尚未达到主动检测混凝土结构已经存在的缺陷和各种性能指标(如强度)的目的。文献［6］中提出了基于压电埋入式敏感模块的超声检测方法，该方法使用一定频率的脉冲波激励埋入混凝土中的压电陶瓷圆片使其辐射超声波，超声波在传播过程中会携带所经路径上混凝土内部信息，接收此超声波并做分析，从而实现混凝土结构缺陷及各种性能指标的检测。

在基于压电埋入式敏感模块的超声检测方法中，超声波作为混凝土健康状态信息的载体，需要有集中的声指向性和较高的声辐射能量，这有利于提高超声检测的有效距离和精度，而声指向性和能量与激励频率相关，压电陶瓷圆片声辐射平面振动而辐射声波，不同的激励频率又将激发声辐射面不同的振动模态，因此，研究在埋入条件下压电陶瓷激励频率和振动模态对声指向性和能量的影响，找到能激发埋入混凝土中压电陶瓷圆片辐射超声波能量高、指向性集中的频率有着重要的理论和工程意义。

1 压电埋入式混凝土敏感模块

在压电陶瓷圆片的两极焊接上电缆线作为信号线，并在其表面包裹厚1 mm的橡胶层，从而制作成压电敏感元件(直径26 mm)，将压电敏感元件埋入调配好的水泥砂浆中(压电敏感元件埋在模块中部10 cm处)，经过30 d的室温养护后制作成压电埋入式混凝土敏感模块，其内部结构和实物如图1所示。

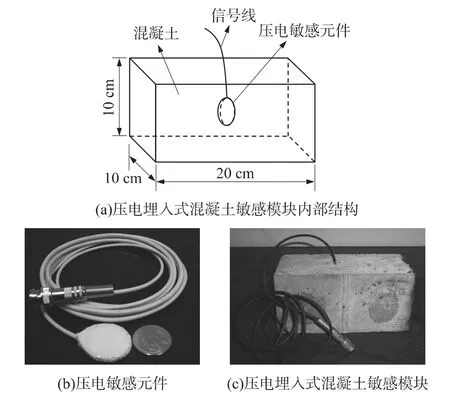
图1 压电埋入式混凝土敏感模块内部结构和实物

压电陶瓷圆片表面的橡胶层可以起到的作用:①橡胶层的绝缘性可以避免压电陶瓷圆片两极直接接触混凝土(混凝土的导电性)而短路，无法辐射超声波;②橡胶层良好的压缩性使得压电陶瓷圆片有较好的振动空间，减小混凝土夹持力对其振动模态的影响，从而将埋入混凝土中的压电陶瓷圆片振动模态看成其在自由状态下振动模态;橡胶层良好的压缩性还避免了混凝土凝固过程中收缩应力损伤压电陶瓷圆片。

2 激励频率与声指向性理论

由于超声检测所涉及的声场范围一般在远场区［7］，本文对声场指向性的研究也只在远场区。将压电陶瓷圆片沿其平面轴向振动看作理想活塞声源，其平面上每一点等效为单一点声源，且各点以相同的振幅作简谐振动，同时辐射出声波，超声波在介质中传播过程中，将形成具有一定指向性的声场，并可用声场指向性函数描述，对于发射响应而言，指向性函数是描述辐射声场(自由远场)的空间分布函数［9］。归一化的指向性函数为［8］

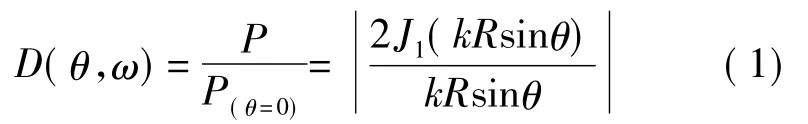
式中，θ为方位角，ω为声波圆频率(与激励频率相关)，P为等效各点声源在声场中某点叠加的声压值，P(θ=0)为主波束轴心方向上(θ=0)的声压值，J1为一阶贝塞尔函数，k=ω/c0为波数，c0为超声波在介质中传播的速度，R为声源半径。

在指向性函数中，对某一平面活塞声源，当方位角θ确定后，声场指向性受激励频率的影响，随着对活塞声源激励频率的增加，辐射到混凝土中的超声波声场指向性越集中［9］。超声波是由于压电陶瓷圆片声辐射平面振动而产生，因此对于埋入混凝土中的压电陶瓷圆片，研究频率与声场指向性和能量的关系，需进一步研究在某激励频率下，压电陶瓷圆片声辐射面的振动模态对声场指向性和能量的影响，据此验证理论结果的合理性，并找到能激励压电陶瓷圆片辐射的超声波声场指向性集中、能量高的频率。

3 压电陶瓷圆片有限元模态分析

压电陶瓷圆片模态分析可确定其各阶模态振型及相应的固有频率，直接观察到压电陶瓷声辐射平面的振动情况，找到影响声指向性和能量的原因;并且在各阶固有频率处压电陶瓷圆片辐射声能量将达到一个极值点。典型的无阻尼模态分析求解的基本方程是经典的特征值问题［10－11］:

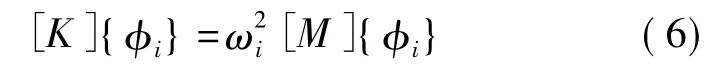
式中各符号的含义:［K］:刚度矩阵;{φi}:第i阶模态的振型向量;［M］:质量矩阵;ωi:第i阶模态的固有频率。

图2所示为利用Ansys软件仿真获得的压电陶瓷圆片一阶到四阶模态振型图，表1所示为前四阶固有频率和振型描述。

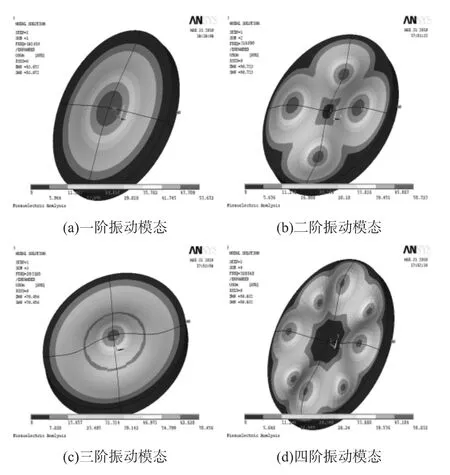
图2 压电陶瓷圆片的模态振型图

在理论探讨中把压电陶瓷圆片看作理想活塞声源，其声辐射平面上等效各点声源有相同的振幅，但如图2模态振型和表1模态描述所示，压电陶瓷圆片各阶振动模态不相同，并且声辐射平面上存在振幅极大值点，在二阶和四阶振动模态中有几个振幅极大区域分散在压电陶瓷圆片边缘部分。

4 压电陶瓷圆片辐射声指向性和能量

试验中制作了三组相同的压电埋入式混凝土敏感模块。超声波声场指向性和能量实验测试系统如图3所示，函数信号发生器发出一定频率的脉冲波，脉冲波被分成两路，一路作为触发信号触发示波器采集数据，另一路激励埋入混凝土中的压电陶瓷圆片，使其发射超声波，超声波经过混凝土后被压电超声换能器接收，并经过滤波、取均值后被显示和记录。

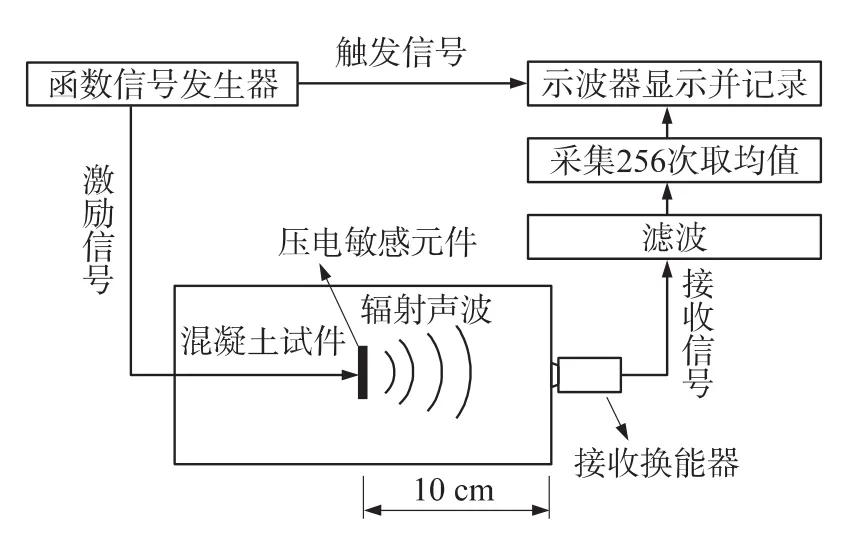
图3 试验测试系统原理框图

在实验中，在离压电敏感元件10 cm处端面内布置了 9 个测点(A，B1，B2，B3，B4，C1，C2，C3，C4)，测点分布如图4所示。由于埋入混凝土中的压电陶瓷圆片各阶固有频率与其在自由状态下相同［12］，利用接收型压电超声换能器测量了在各阶固有频率下各测点的电压值，并在每个频率下取在三组模块上相同位置测点测得三个数据的平均值(单位mV)，如表2所示。在一阶固有频率下，主波束轴心位置电压值最大，即该点的声能最大;而在模态分析中，一阶振动模态下，压电陶瓷圆片声辐射平面振幅最大值区域最宽，且集中在中心位置，从而声辐射能量最大，而在二阶到四阶固有频率下，振动位移极大值区域都相对较小且分散，因此辐射能量小。

图4 测点分布示意图

表2 各阶固有频率下各测点电压幅值

由于某测点的电压值与声压值呈线性关系［13］，并根据归一化声场指向性函数定义，计算并绘制了各阶固有频率下声场指向性对比曲线图(由于声场的对称性，取 A，B1，B4，C1，C4值对比)，如图 5 所示。在一阶和三阶模态分析中，声辐射平面最大振幅区域都集中在中心位置，并在实验中，随着激励频率的增加，声场指向性更集中;在四阶与二阶固有频率下，由于声辐射面振幅极大值区变得分散，即使随着频率增加，声场指向性也变得发散。这说明不同激励频率引起的压电陶瓷圆片不同的振动模态对声场指向性有影响。理论中将声源振动面等效为振幅相等的单一点声源的叠加所得随着频率的增加，声场指向性越集中的结论与实际偏差较大，需考虑振动模态对声场指向性的影响。

图5 各阶固有频率下声指向性对比曲线图

如图6所示，压电陶瓷圆片各阶固有频率下理论与实验声场指向性对比图。由图分析可得，由于将压电陶瓷圆片声辐射面等效为振幅相等的单一点声源的叠加，忽略各阶振动模态下振幅极大值区域的集中程度，使得声场指向性理论结果比实验结果发散，只有在四阶模态下，振幅极大值区域分散在压电陶瓷圆片边缘八个区域时，其声场指向性理论值才与实验值的基本一致。

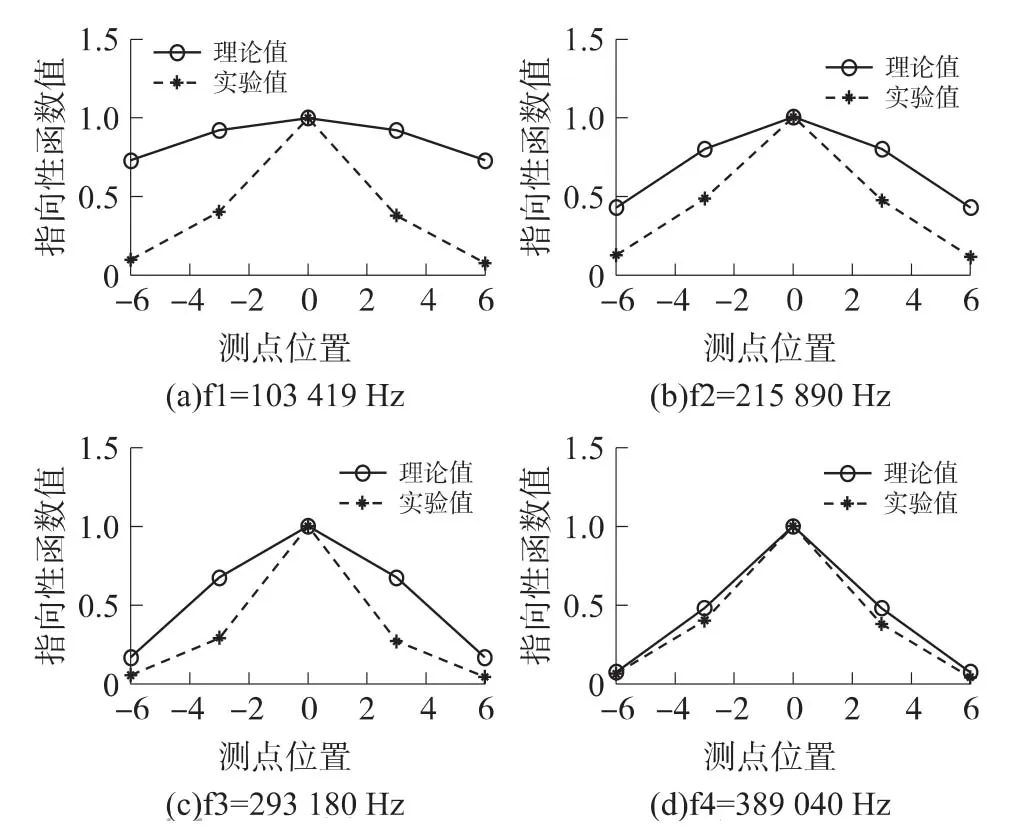
图6 各阶固有频率下理论与实验分析声指向性对比图

结合分析表2和图5所示，三阶固有频率下声场指向性最集中，但声辐射能量比一阶固有频率下小，二阶和四阶固有频率下声辐射能量也比一阶小，并且声指向性也比一阶略微发散，因此，综合考虑声指向性和能量，在一阶固有频率下压电陶瓷圆片辐射声波具有最大的声能和较集中的声指向性，更适用于超声检测。

5 结论

通过有限元模态分析，得到了埋入混凝土中压电陶瓷圆片一阶到四阶的振动模态及其固有频率，发现压电陶瓷圆片声辐射平面具有振幅极大值区域，并且不同振动模态下，极大值区域分布不同，这与声场指向性理论中将压电陶瓷圆片声辐射面等效为有相同振幅的单一点声源的叠加不同;埋入混凝土中压电陶瓷圆片在各阶固有频率下声场指向性和能量实验表明:在声场指向性理论分析中忽略不同频率下压电陶瓷圆片声辐射面振动模态不同，使得在各阶固有频率下压电陶瓷圆片辐射声指向性变化规律偏离实际较大，而在相同频率下声指向性理论结果比实验结果发散;在各阶固有频率下，压电陶瓷圆片辐射声指向性集中，但在一阶固有频率下声能最高，因此更适用于超声检测。

［1］吴慧敏.结构混凝土现场检测新技术——混凝土非破损检测［M］.湖南:湖南大学出版社，1998.7.

［2］Gu H，Song G，Dhonde H，et al.Early Age Strength Monitoring of Concrete Structures Using Embedded Smart Piezoelectric Transducers-art［J］.no.61790H.Advanced Sensor Technologies for Nondestructive Evaluation and Structural Health MonitoringⅡ6179:H1790－H1790，2006.

［3］Wen Y，Li P，Huang S.Study on the Readout of Piezoelectric Distributed Sensing Network Embedded in Concrete［J］.SPIE，1998，330:642－671.

［4］田卉，文玉梅，李平，等.埋人混凝土结构中的PZT压电陶瓷温度特性研究［J］.传感技术学报，2007，20(9):1977－1982.

［5］Chen Y，Wen Y，Li P.Characterization of Concrete Stress by Measuring Dissipation Factors of Embedded Piezoelectric Ceramic Disc［J］.Proceedings ofSPIE:Sensors and SmartStructures Technologies forCivil，Mechanicaland Aerospace Systems，Santiago，U.S，March，2005，5765:30－41.

［6］安占营.基于压电埋入式模块的混凝土声检测研究［D］.重庆大学，2010.4.

［7］吴新璇.混凝土无损检测技术手册［M］.北京:人民交通出版社，2003.1.

［8］杜功焕，朱哲民，龚秀芬.声学基础［M］.南京:南京大学出版社，2001.8.

［9］B A奥尔特，著.孙承平，译.固体中的声场和波［M］.北京:科学出版社，1982.12.

［10］任重.ANSYS实用分析教程［M］.北京:北京大学出版社，2003.2.

［11］姜德义，郑拯宇，李林，等.压电陶瓷片耦合振动模态的Ansys模拟分析［J］.传感技术学报，2003，12(4):452－456.

［12］Wen Y，Chen Y，Li P.Characterization of PZT Ceramic Transducer Embedded in Concrete［J］.Sensors ＆ Actuators:A.Physical，2006，128(1):116－124.

［13］美国无损检测学会.美国无损检测手册:超声卷［M］.北京:世界图书出版公司北京公司，1996.1.