微陀螺梳齿静电驱动力的计算方法
2011-10-19姚峰林高世桥
姚峰林,高世桥
(1.北京理工大学 机电学院,北京 100081;2.太原科技大学机电学院,太原 030024)
微机械陀螺是20世纪80年代后期发展起来的一种测量角速度或角位移的惯性传感器,是微机电系统(MEMS)技术应用的一个重要方面[1]。微机械陀螺与传统陀螺相比,具有体积小、重量轻、成本低、功耗低、能适用于较为恶劣的环境、可以批量生产、易与CMOS接口电路集成、以及数字化和智能化等特点[2-3]。微机械陀螺的优良特性决定了它具有广阔的应用前景与商业和军事价值[4]。目前,大多数微机械陀螺还主要应用于中低精度场合,由于高精度应用场合的需求,需要研制出高性能高精度的微机械陀螺[5]。
由于静电驱动力是研究微结构静态、动态力学的基础,它将影响微机械陀螺的信噪比和灵敏度,准确计算微结构静电力是合理、准确地分析、设计静电驱动微结构的前提条件[6]。目前的静电力的计算大多是基于无限大平模型的[7-8],实际上,在微陀螺梳齿的分析中,无限大平板理论应用在有限尺度的电极上是近似的。赵剑等采用复变函数法推导了考虑边缘效应的两个近似简化公式,并作了精度分析[9]。但梳齿结构上具有拐角结构,在电容和静电力计算时,需要考虑这一特殊性。
1 静电驱动的原理
由电容式微机械陀螺仪工作原理可知,要想使陀螺仪工作,陀螺仪接口电路必须使陀螺仪振动质量块在驱动模态方向振动[10]。对于静电驱动微机械陀螺仪而言,主要利用静电力来达到驱动微陀螺仪质量块振动的目的。当在两导体结构间施加一定的电压时,导体表面分别携带有数量相等的正、负电荷,正、负电荷之间存在库仑力作用[11]。采用差动梳齿驱动器是驱动微机械陀螺的常见方式,也就是直流(如图1所示的Vdc)加交流(如图1所示的Vacsin(ωdt))的推挽驱动[12],差动梳齿驱动器的结构如图5、图6所示。

图1 差动梳齿驱动器示意图(左)与照片(右)
2 静电驱动力的计算
微梳齿结构是基于平行板电容模型的,因此计算平行板电容的静电力大多采用此模型,如图2所示,平行板电容器边长为a、b,板间距为d。假设下极板固定,上极板通常有两种运动方式:一种为相对下极板垂直运动,一种为相对下极板水平运动。而对于实际情况下的微梳齿结构来说,梳齿的长宽高及梳齿间距相对来说都是有限长度的。当两极间加上反向电压发生顺向移动时,齿间会因反向电压的作用产生电容,此时考虑梳齿的厚度,以及齿根部拐角部分的影响,并不能简单的取理想情况下的无限大平行板模型来进行运算,这时要考虑微梳齿结构间的边缘效应以及拐角效应。另外,由于陀螺结构的特殊性,只能使梳齿结构在平行于齿顺向进行运动,这里运动的方向为X。
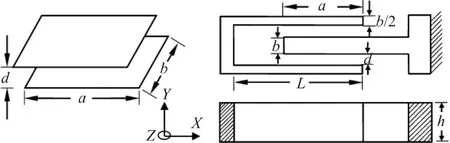
图2 平行板模型与微结构的梳齿模型对比
2.1 无限大平板模型
无限大平板模型是目前微结构中应用最多的,此模型假设a、b相对于d无限大,即忽略电容的边缘效应,根据电容定义,可求得:
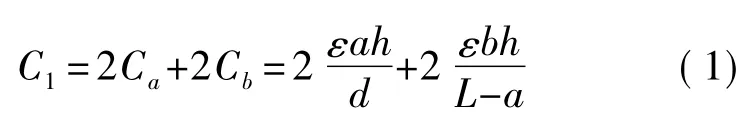
利用电势能和虚位移原理可求得平行运动静电力为

对于微机械陀螺中的梳齿结构,尺度为微米量级甚至更小,而且由于加工条件限制,a、b不能过长,而间距d不能太小,d相对于a、b不能取无限大,一般不能简单直接应用上述公式,而需要考虑边缘效应带来的影响[9]。因此针对实际的问题,需在无限大平行板电容模型的基础上,考虑各类效应的影响。
2.2 考虑边缘效应模型
通常微机械陀螺结构都采用高纵深比工艺加工,因此厚度方向可视为相对齿宽和间距无限大,这从另一方面说明了讨论二维模型的可行性。从图3中A所指部分,在梳齿的边缘部分电势的变化非常明显,这与无限大模型的电场均匀分布模型具有明显的区别。可以看出梳齿边缘的电势分布是相当可观的,对微陀螺的驱动力会有明显的影响,使用无限大平板模型一定会带来误差。

图3 微陀螺梳齿结构的电势分布和Ansys模型
应用保角变换是求解二维平行板电容的一种典型方法,相关文献[9]给出了考虑边缘电场的电容计算式,由于在求解过程中作了近似处理,因此该解析式也是近似解:

其中,

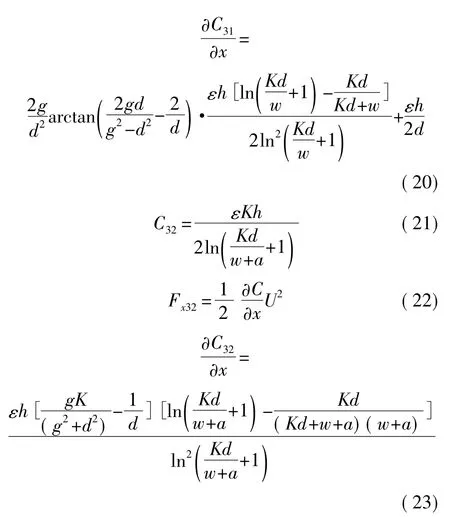
因此梳齿横向静电力为
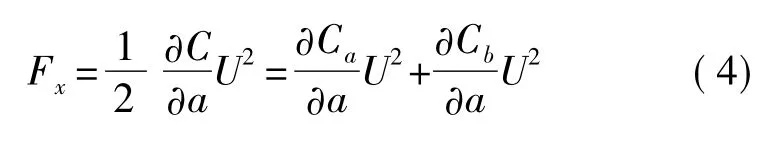
其中,
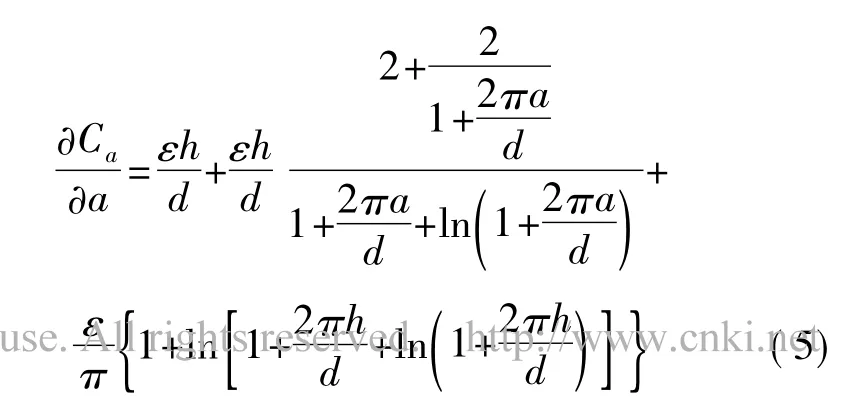

2.3 梳状结构电容的拐角效应
从图3中B所指部分,可以看出进入梳齿槽内的梳齿边缘的电势分布也是不均匀的,非均匀电场,这里把进入梳齿槽内部的梳齿边缘与槽之间的部分叫做拐角如图4所示。使用无限大平板模型来计算微陀螺的驱动力必然会有一定的误差。考虑边缘效应时,只是简单的从平行板边缘效应出发,将梳齿结构近似成平行板电容器的并联,加入边缘附加项。这些模型都忽略了梳齿自身的结构特点,因此这里提出一种新的电容计算方法,并与以上模型进行对比。
为了计算拐角效应的影响[13],取梳齿的1/4进行分析如图4所示,利用非线性电容特性公式

其中,ε(l)为区域间填充介质的介电常数,这里介质为空气,因此ε(l)=ε0;S(l)为等势面,只要确定区域内的等势面函数,就可以求出区域的电容。
下面建立几种拐角处的近似电势场模型来计算电容,并与无限大平板模型和考虑边缘效应模型进行对比,这里不考虑厚度方向的边缘效应影响。
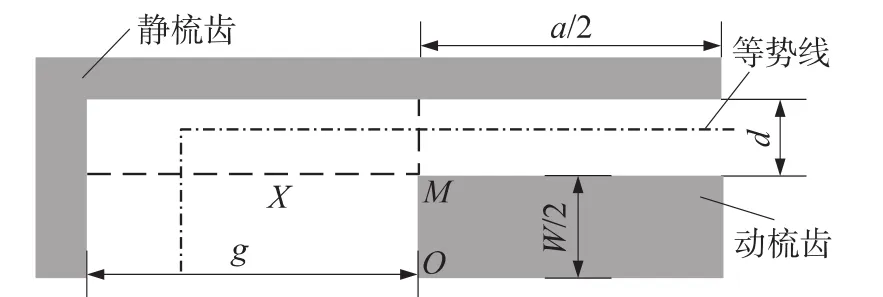
图4 拐角模型示意图
2.3.1 矩形等势线
在g、d上取等分点,作矩形等势线,如图4所示,在设计中交叠长度a很大,所以可以认为电容由两部分组成,一部分为a/2的平行板电容,一部分为拐角和齿间与根部电容。
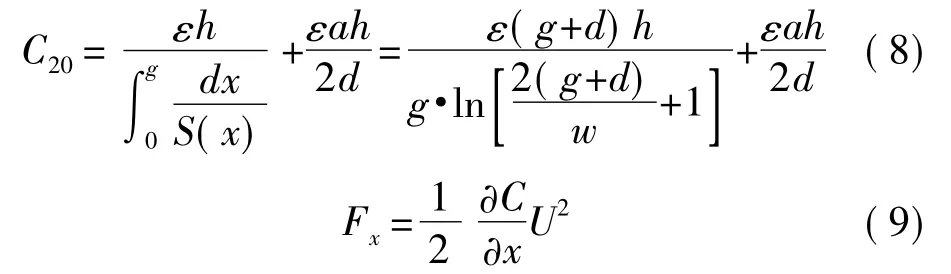
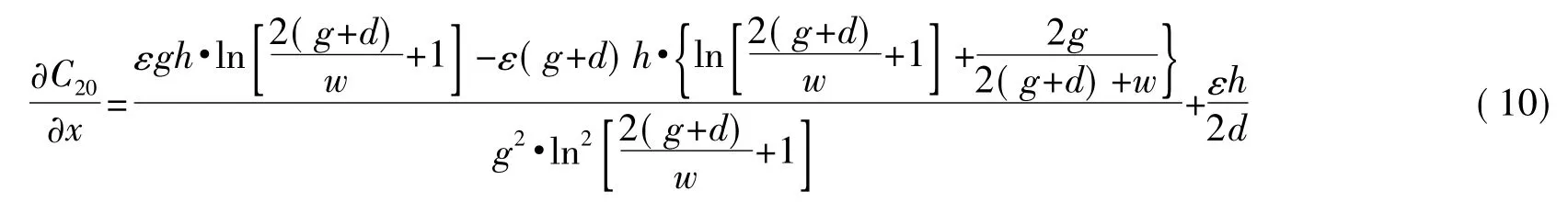
2.3.2 圆弧等势线
在g、d上取等分点,作圆弧等势线如图5所示。

图5 拐角模型示意图

若S(x)计及a/2段,则
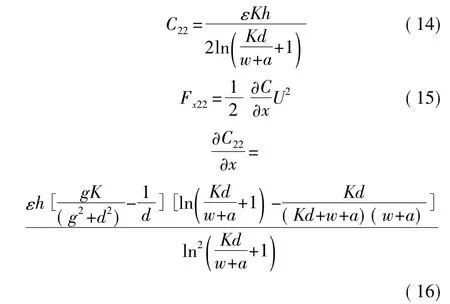
2.3.3 与g无关的模型
注意到模拟中电势场在一定范围内与位移基本无关的特点,建立与g无关的模型,利用式(2)中的结论,取g=Nd
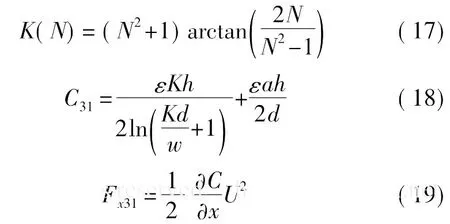
2.3.4 圆等势线
以M为圆心在拐角处作1/4圆作为等势线,如图6所示。
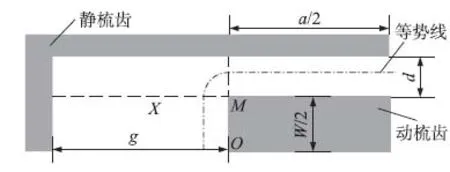
图6 拐角模型示意图
若S(x)不计及a/2段,即认为电容仍有两部分构成,则

若S(x)计及a/2段,则

将以上4种模型与无限大平板模型、边缘效应、拐角效应模型和有限元分析进行对比,梳齿结构的参数取h=55 μm,b=4.2 μm,d=3 μm,L=87 μm,齿数为N=1184时,计算间距g不同时电容的值,如图7所示。齿顶与齿根的距离变化时静电力的大小如图8所示。
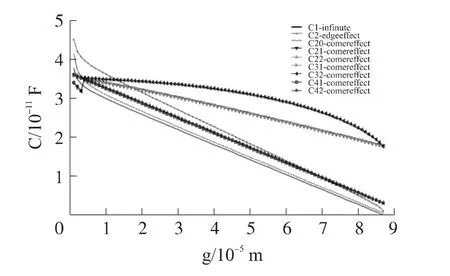
图7 电容随间距变化图
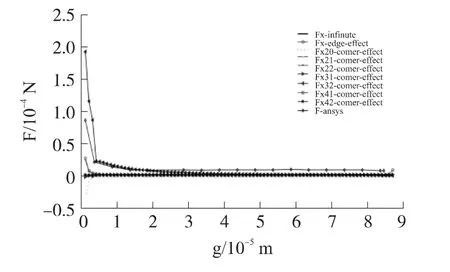
图8 静电力随间距变化图
静电力直接影响微陀螺的驱动振幅,进而影响微陀螺加速度的检测值。图9列出了考虑边缘效应和拐角效应时和不考虑边缘效应时振动的振动曲线。
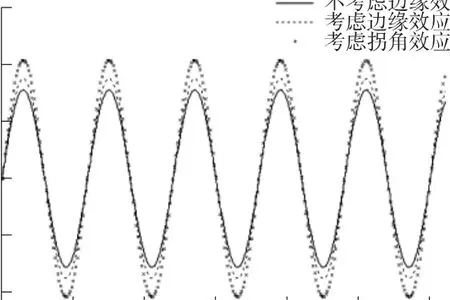
图9 不同驱动电压下振幅变化规律
3 结论
由图7中可以看出,各种模型的计算的电容结果表明,随着梳齿间距的缩小,梳齿电容大多是线性增加的,但当梳齿的间距小于5 μm后,电容产生了迅速的增加。其中,无限大平板模型计算出的电容是最小的,考虑边缘效应的电容值要比无限大平板模型要大,拐角效应模型比边缘效应和无限大平板的模型的结果都要大。对于C20模型,由于选择的是g和d的中点作矩形等势线,故而在静梳齿和动梳齿不充分接近的时候(>3 μm),这种模型数值偏小;对于C21和C31模型,也采用了g和d的中点作弧等势线,故而在静梳齿和动梳齿不充分接近的时候(间距>10 μm),这种模型数值偏大;对于C22和C32模型,是在C21和C31模型上对直线段等势面方程的变形,由于这种假设的几何模型只限于在梳齿间距充分小的时候,所以在间距较大时也有较大的偏差,但是对于C21,C31,C22和C32四种模型在10 μm左右的范围内却其它模型数值接近,同时当梳齿间距<5 μm后数值发生跳变;对于C41和C42模型,是对d的中点单独作1/4圆等势线,这种模型的电容数值比较稳定,但是随着交叠长度增加,它的值却小于了边缘效应值。
从图8中可以看出,当动静梳齿间距大于5 μm时,梳齿间的静电力在X轴方向随间距不会有明显变化;但当梳齿间距进入5 μm阶断后,静电力产生了迅速的增加。考虑边缘效应的模型要比无限大平板模型计算出的静电力要大,边缘效应模型在梳齿未交叠之前就有静电吸引力的作用,这充分体现了边缘效应的作用;考虑拐角效应的静电力Fx21,Fx22,Fx31,Fx32模型比无限大平板模型的Fx-infinite和边缘效应模型的Fx-edge-effect都要大;考虑拐角效应的Fx41,Fx42在间距较大时与无限大平板模型接近,但当梳齿充分接近时,不能反映静电力的非线性增长;Fx21,Fx31在梳齿充分接近时(<5 μm),静电力的变化趋势有误,这与把等势场主观地分成两块有关;Fx41,Fx42静电力的变化趋势也有误,这与两种模型的假定是等势场的线性变化是相关的。
考虑边缘效应和拐角效应的电容和静电力结果均比理想结果要大,并且更接近Ansys模拟结果。这说明在微尺度条件下静电场的边缘效应和拐角效应应当在设计和计算时充分考虑,拐角效应的各种模型也有局限性。另外,间距无限近时,电容和静电力都迅速增大,此时动齿和定齿之间会产生吸合效应。因此对于使用梳齿结构作为陀螺驱动,需要确定活动位移以及静电电压范围,保证其工作在准线性范围内。
[1]蒋庆华,苑伟政,常洪龙,等.一种改进的振动式微机械螺驱动电路[J].传感技术学报,2008,21(3):536-538.
[2]熊斌,车录锋,黄小振,等.一种微机械陀螺自激驱动方式的电学模拟[J].仪器仪表学报,2003,24(2):190-192,200.
[3]王玲,刘俊,石云波.微小差分电容检测电路设计[J].传感技术学报,2006,19(6):2529-2531.
[4]车录锋,黄小振,熊斌,等.振动式微机械陀螺的等效电学模型[J].机械工程学报,2003,39(3):117-120,125.
[5]张霞,郑旭东,王昊,等.微机械陀螺的建模与仿真[J].浙江大学学报(工学版),2009,43(4):646-650.
[6]王亚强,王跃林,丁纯,等.微机械谐振传感器的闭环恒幅驱动电路研究[J].仪器仪表学报,1999,20(4):351-355.
[7]YOUNIS M I,ABDEL R E,NAYFEH A.A Reduced-Order Model for Electrically Actuated Microbeam-Based MEMS[J].Microelectromechanical Systems,2003,12(5):672-680.
[8]RAHMAN A M,YOUNIS I M,NAYFEH H A.Characterization of the Mechanical Behavior of an Electrically Actuated Microbeam[J].Journal of Micromechanics and Microengineering,2002,12(6):760-766.
[9]赵剑,贾建援,王洪喜.计及边缘效应的静电驱动微结构静电力计算[J].微纳电子技术,2006,43(2):95-97.
[10]罗跃生.硅微型梳状线振动驱动式陀螺仪工作的微分方程模型[J].哈尔滨工程大学学报,2003.24(1):49-53.
[11]茅盘松,王修伦.微机械结构的微静电驱动[J].电子器件,1995,18(1):20-23.
[12]王存超,苏岩,王寿荣.硅微振动陀螺仪驱动器自激驱动研究[J].传感技术学报,2006,19(2):364-370.
[13]高世桥.微机电系统力学[M].北京:国防工业出版社.2008.106-110.
