基于MATLAB的锁相环非线性分析
2011-10-18刘科江
刘科江
(电子科技大学电子工程学院,四川 成都 611731)
基于MATLAB的锁相环非线性分析
刘科江
(电子科技大学电子工程学院,四川 成都 611731)
锁相环通常工作在捕捉和跟踪两种模式下的一种。在捕捉模式下,锁相环试图使 VCO的输出信号与输入信号在频率和相位上同步。但是在捕捉模式下,VCO的输出信号与输入信号的相位差可能相当大,锁相环此时工作在非线性状态,需要用非线性模型来进行分析。分析非线性模型是很困难的,常常需要进行仿真。利用 MATLAB工具,使用微分方程法研究锁相环系统的非线性特性。
锁相环;微分方程法;非线性;MATLAB
锁相环是一种相位反馈的闭环自动控制系统,环路锁定之后,平均稳态频差等于零,稳态相差为固定值,锁相环的这一重要特征使其在电视、通信、雷达、遥测遥感、测量仪表,特别是在人造卫星和宇宙飞船的无线电系统中,得到了广泛应用。近年来,锁相环路的研究日趋深入,应用更加广泛。由于鉴相器模型是非线性的,所以锁相环是一个非线性系统,很难用传统的解析方法来分析,因而我们求助于仿真。下面我们使用微分方程法来分析一个二阶锁相环的非线性特性。
(一)锁相环模型
1.锁相环框图
锁相环基本模型如图1所示。假设输入信号为

而压控振荡器的输出信号表达式假设为
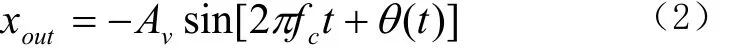
锁相环的就是使 VCO的相位与输入信号的相位同步,使得他们的相位差很小

图1 锁相环框图
2.鉴相器模型
开发锁相环模型的第一步就是建立鉴相器的模型。鉴相器的特性在很大程度上决定着锁相环的工作特性。有许多种不同类型的鉴相器,而选择在特定环境下所使用的鉴相器模型取决于具体的应用。最常见的鉴相器模型就是正弦鉴相器,它的输出与输入信号的相位差的正弦成正比。正弦鉴相器可以看成是有一个乘法器和一个低通滤波器组成的,则鉴相器输出信号为
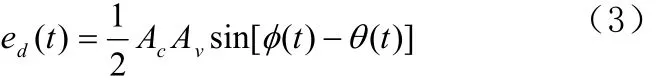
其中, )()(tt− 称为相位差。我们希望VCO的输出相位是输入相位的一个估计,因此,锁相环正常工作要求相位差趋于零。在稳态时,相位差是否为零取决于输入信号和环路滤波器。使用传递函数为 F(s)而单位冲击响应为 f(t) 的环路滤波器,对鉴相器输出进行滤波。这样,VCO的输入为
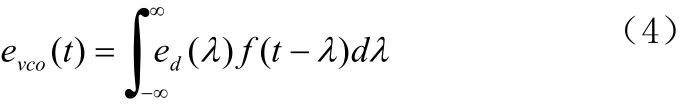
由定义,VCO的输出频率偏差与VCO的输入信号成正比,这样

式中,Kd是VCO常数,单位HzV。带入上面式子可得到

式中cvdAAKG= 。
3.非线性相位模型
从 6式可以看出, )(t与 )(t之间的关系与载波频率完全没有关系,因此仿真模型中不需要考虑载波频率。我们要寻找一个能描述 )(t与 )(t之间合适关系的模型。这种模型如图 2所示,称为锁相环非线性相位模型。由于正弦函数是非线性的,所以他是一种非线性模型。这也是一种相位模型,他建立的输入信号相位偏差和 VCO相位偏差之间的关系,而不是建立环路实际输入信号与VCO信号之间的关系。
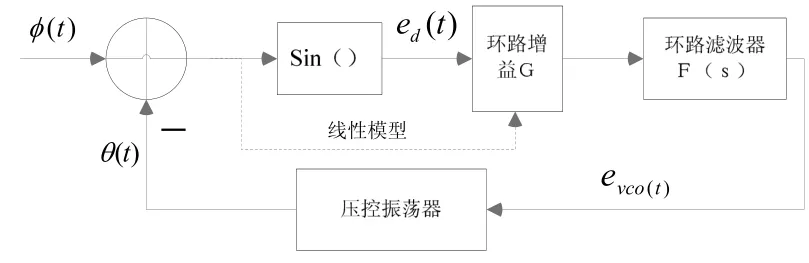
图2 锁相环非线性相位模型
4.线性相位模型和传递函数
若相位差很小,可以做如下近似
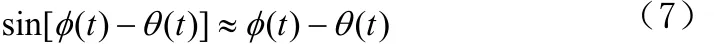
则环路方程变为
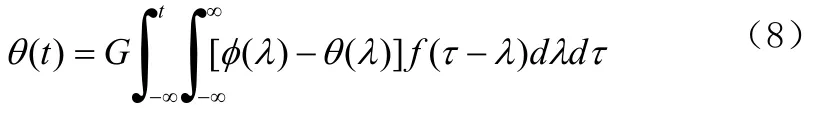
对(8)式做拉普拉斯变换,积分变换相当除以s,时域卷积相当频域相乘,得
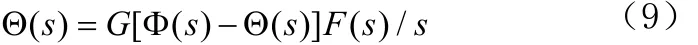
因此,关联VCO相位和输入相位的传递函数H(s)为

(二)仿真
1.二阶锁相环
锁相环的捕捉和跟踪特性很大程度上取决于环路阶数。锁相环实现的阶数等于传递函数H(s)中有限极点的个数。因此,锁相环实现的阶数比环路滤波器传递函数F(s)中极点个数大一,这个多出来的极点就是来及 VCO模型的积分器,下面我们分析一下二阶锁相环。
对于二阶锁相环,环路滤波器的传递函数一般形式是

实际应用中, 远小于1。对于环路线性传递函数,将滤波器传递函数代入式(10)得
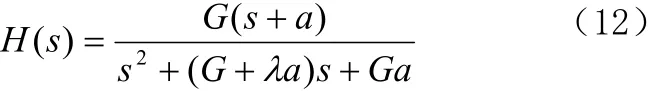
2.仿真流程图
环路滤波器不是一个真分式函数,应用长除法得
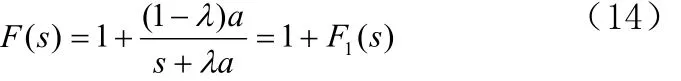
其中就有

其时域表达式为
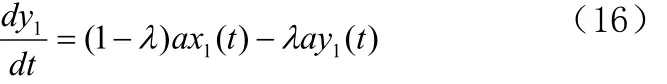
我们可以直接实现滤波器模型,并定义a1=(1−)a,a2=a。可以得到二阶锁相环的信号流程,如图3所示。
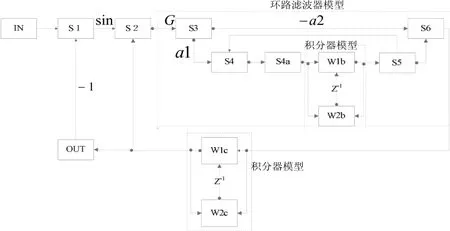
图3 二阶锁相环的信号流图
3.使用微分方程法对锁相环仿真
现在考虑使用微分方程法对锁相环进行仿真。首先导出微分方程。由图2可得
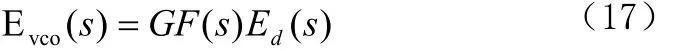
因为图2中锁相环模型中的VCO能用一个积分器表示,于是就有

把式(17)代入式(18),并应用式(11)于环路滤波器,则
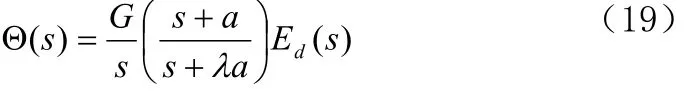
假设二阶环式是“理想的”(即 =0),此问题可以得到一点简化。
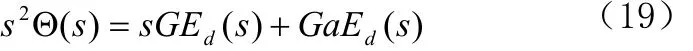
由于乘s等于时域微分,所以得到微分方程
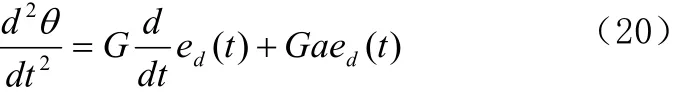
又由定义有

和

于是式子(20)可以写成

式中 )(t是锁相环的相位差,而 )(t是输入信号的相位偏差。
(三)仿真结果及分析
假设这个系统在0tt= 时刻有一个频率阶跃信号,此时,其中fΔ=1MHz。当
=0.1,环路自由振荡频率n=200KHz,则由上面的仿真模型可以得到以下结果。
1.相位误差
稳态相位误差可以用拉普拉斯变换终值定理来计算。环路的闭环相位传递函数为H(s),则相位差传递函数为E(s)=1—H(s),那么利用终值定理可以得到
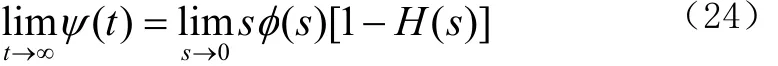
代入以上数据,可以得到 )(∞ = 0.3755 rad,图 4中稳态相位差的结果为0.384516 rad,因此,仿真结果和理论推导结论一致。
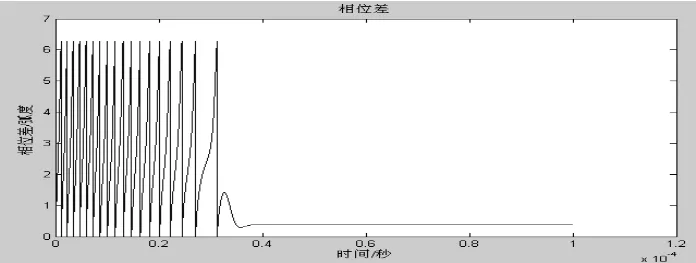
图4 相位差
2.捕获与跟踪过程
图5显示了VCO的输出信号频率的变化过程,能看到在频率捕获过程中的“周期滑动”现象。这是在输入频率的变化大大超过环路的固有频率时,非线性同步器表现出来的特性。在图中我们也能看到相位锁定时所需要的时间。
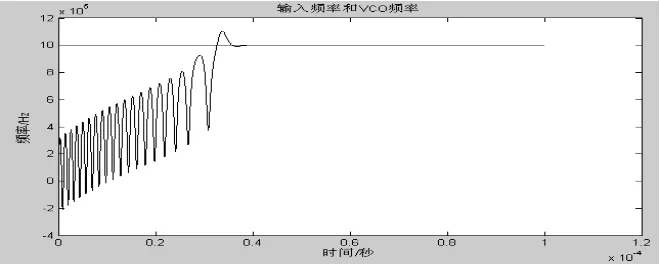
图5 输入频率和VCO输出频率
(四)结语
本文通过建立锁相环的非线性相位模型,使用微分方程法,利用MATLAB仿真工具,从定量上分析了锁相环的非线性相位特性。从仿真图形可以看到,仿真结果与理论分析结果相吻合。通过这种分析方法,能为锁相环设计提供定量的分析,有助于电路的优化设计。
[1] Donald R.Stephens. Phase-locked loops for wireless communications [M].New York:Kluwer Academic Publisher,2002:5-7.
[2] Dan H.Wolaver.Phase-Locked Loop Circuit Design[M].New Jersey:Prentice Hall,1991:8-11.
[3] Roland E. Best.Phase-Locked Loops Design,simulation,and Application[M].5.New York .The McGraw-Hill Companies,2003:35-36.
[4] Tapio Rapinoja.Behavioral model based simulation methods for charge-pump PLL[C]//The IEEE International Baltic Electronics Conference,Tallinn:IEEE,2006,10:1-4.
[5] Qi Jing, See-Mei Chan.Characterizing PLL Jitter from power supply fluctuation using mixed-signal simulations[C]//The IEEE International Quality Electronic Design,Penang:IEEE,2010,8:112-117.
TP273
A
1008-1151(2011)05-0060-02
2011-02-18
刘科江(1985-),男,电子科技大学电子工程学院在读硕士,研究方向微波线性和非线性电路系统。
