小波包与贝叶斯LS-SVM在石油价格预测中的应用

王欣冉,邢永丽,巨程晖

（中国地质大学(北京)信息工程学院,北京100083）

小波包与贝叶斯LS-SVM在石油价格预测中的应用

王欣冉,邢永丽,巨程晖

（中国地质大学(北京)信息工程学院,北京100083）

掌握国际石油价格变化趋势，可以为决策者提供决策依据。文章提出了基于小波包和贝叶斯推断的最小二乘支持向量机石油价格预测方案。对石油价格时间序列进行小波包分解与重构，采用贝叶斯推断对得到的各近似序列和各细节序列进行最小二乘支持向量机模型参数优化，再分别利用优化了的模型进行预测，合成得到最终预测结果。对美国纽约商品交易所原油价格进行仿真实验，结果表明该方法很好地改善了石油价格预测模型的运行速度与预测精度。

小波包变换；最小二乘支持向量机；贝叶斯推断；石油价格预测

0 引言

石油主要被用来作为燃油和汽油，是目前世界上重要的能源之一,它直接影响到各国国民经济和国家安全。自1998年我国国内油价与国际油价接轨以来,国际原油价格水平对我国石油、石化企业的发展有着直接的影响。随着我国对石油消费需求的不断增加,石油价格趋势的预测对于国家调控及制定能源政策的意义愈加重要。

小波变换具有多尺度分析的特点，并能够表征信号局部特征，可以有效的提取时序变化特征。Suykens所提出的最小二乘支持向量机回归方法[1]克服了局部极小点和维数灾难问题,具有很好的泛化能力。但在确定LS-SVM核函数参数、正规化参数时采用的交叉验证法计算复杂耗时，不适合大样本数据。近年来,采用贝叶斯推断的逻辑一致性和简单灵活性来进行LS-SVM的参数优化[2]，取得了很好的效果。据此，本文结合小波包变换和贝叶斯证据框架下的LS-SVM方法对石油期货价格预测进行研究，并以美国纽约商品交易所原油价格预测为例来检验方法的有效性和可行性。

1 预测理论方法

1.1 小波包理论

小波变换存在着在高频频段其频率分辨率较差、低频频段其时间分辨率较差的缺陷。小波包变换是基于小波变换的进一步发展，相比于小波可以更灵活、更精细地提取不同尺度上时间序列的变化特征,有利于提高预测精度。它将频带进行多层次划分，对多分辨分析没有细分的高频部分进一步分解，并可以根据被分析信号的特征，自适应的选择相应频带，使之与信号频谱相匹配，从而提高了时频分辨率。这有利于提取股指数据中高频波动项的特征信息，避免了干扰对趋势项的预测。

小波包的分解算法和重构算法[3]如下：

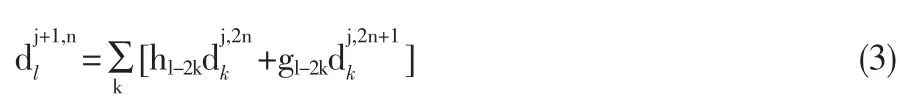
1.2 最小二乘支持向量机算法

LS-SVM的算法[5]如下:

给定训练样本集(xi,yi)，i=1,2,…，l，其中xi∈Rn为输入数据,yi∈R为输出数据。利用能够折中考虑回归函数经验风险和泛化能力的结构风险最小化准则构造如下最小目标函数及其约束条件:

其中:准(·)为核空间映射函数，它将输入数据xi映射到高维空间F.ω∈F为权向量，b∈R为偏置量。ei为误差变量，γ为正则化参数。建立Lagrange函数：

其中αi为Lagrange乘子。对于i=1,2,…，l，分别对上式中ei,αi,ω,b求偏导，再消去ei和ω可得如下线性方程组：

AHP法是一种将与决策有关的元素分解成目标、准则、方案等层次权重决策的分析方法，既包含了专家对指标重要性的主观判断，又遵循了指标间的客观关系[9]。具体步骤如下：

引入满足Mercer条件的核函数K(xi,xj)=准(xi)T准(xj)将变换空间中的内积转化为原空间中某个函数的计算，从而间接求解核空间映射准。有多种核函数K(xi,xj)可供选择，本文采用高斯核函数:

解式（6）线性方程组求得和，得到最小二乘支持向量机回归模型：

1.3 贝叶斯推断参数优化

标准LS-SVM中一般采用交叉验证法来确定较优的参数(γ,σ2)，但当样本数据量较大时，运行较为复杂。因此，本文采用贝叶斯推断方法[7]，将样本分为训练集和验证集，通过对训练集进行贝叶斯推断来优化参数(γ,σ2)，进而提高运行效率。贝叶斯推断通过最大化参数分布的后验,从而得到最佳参数值。推断过程可分为三步:

第一步：推断ω和b

设D为训练集，H为基于核函数的模型，由贝叶斯准则可得:

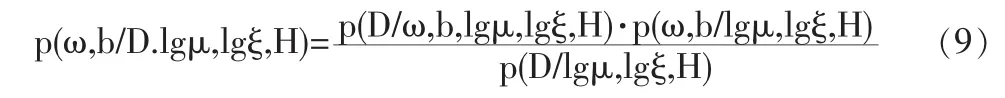
式中,p(D/ω,b,lgμ,lgξ,H)为似然函数；p(ω,b/lgμ,lgξ,H)为ω和b的联合先验概率；p(D/lgμ,lgξ,H)为不受参数ω和b约束的归一化因子。通过最小化式(9)的负对数可以获得最大后验估计ωmp和bmp[8]。

第二步：推断正则化参数γ

设p(lgμ,lgξ/H)=p(lgξ/H)·p(lgμ/H)，由贝叶斯推断有:

式中,p(D/lgμ,lgξ,H)似然函数即为第一步推断中的归一化因子，从而求得正则化参数γ=ξ/μ。

第三步：推断核函数参数σ2

应用贝叶斯法则推断模型Hj，有:

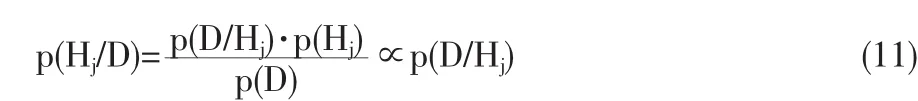
式中似然函数p(Hj/D)为第二步推断中的归一化因子，通过最大化p(D/Hj)，计算并比较相应Hj模型的后验概率，最大值对应的即为最优核参数。

1.4 小波包与LS-SVM石油价格预测模型

基于小波包与贝叶斯最小二乘支持向量机的石油价格预测算法如下:

(1)对训练集和测试集的原数据进行归一化处理；

(2)将处理后的数据进行小波包分解，并将分解所得的最低层各近似部分和各细节部分分别单支重构到原分辨率上；

(3)确定输入节点数，以滚动预测方式分别对训练集每个频率通道的子序列进行步骤4)～7)的操作；

(4)设定参数(γ,σ2)的初始值，用训练集对最小二乘支持向量机进行训练，通过贝叶斯推断优化模型参数ω和b；

(5)通过贝叶斯推断优化正则化参数γ；

(6)通过贝叶斯推断优化核参数σ2；

(7)用所求得的参数重新训练最小二乘支持向量机,选择最优模型及输入节点数；

(8)用最优模型分别对测试集各频率通道的子序列进行预测；

(9)合成各子序列的预测值并反归一化，得到最终预测结果。

2 实例分析

2.1 数据整理

表1 预测模型平均绝对百分比误差与相关系数比较

采用美国纽约商品交易所(New York Mercantile Exchange，NYMEX)2004年1月～2008年1月共1021个交易日的原油期货价格作为研究对象，来检验该预测算法，见图1（单位：美元/桶）。首先将收集数据采用MATLAB命令premnmx进行归一化处理，然后对所得数据进行小波包分解。经实验比较，采用预测效果最好的db2小波基进行三层分解。将分解得到的各近似部分和各细节部分分别单支重构到原级别上,见图2。将原数据样本划分为前1000个训练样本和后21个检验样本，初始化γ=10，σ2=2分别对各个频率通道的子序列采用滚动预测方式，得到输入节点数7及对应的最优模型。对检验样本即2008年1月2日～1月31日共21个交易日的原油期货价格进行预测，合成各个子序列预测结果得到最终预测值。

为了检验实验一：结合小波包变换与贝叶斯框架下LSSVM模型在石油价格预测的有效性，本文将归一化的训练样本作为输入样本做了实验二：基于标准LS-SVM的石油价格预测，输入节点数同样为7；实验三：基于RBF神经网络的石油价格预测，RBF网络采用网络的输入节点数为6，隐含层神经元为10个，输出节点数为1。利用MATLAB7.1和LSSVMlab1.5[9]工具箱，以平均绝对百分比误差和相关系数为预测水平的评价标准。

平均绝对百分比误差公式为：

Pearson相关系数公式为：

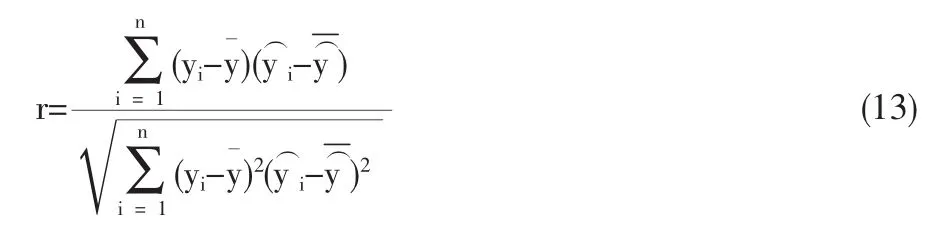
2.2 结果分析

表1为三种预测模型的MAPE误差与相关系数比较。

由结果可得，基于标准LS-SVM的预测误差要比基于RBF神经网络的小,主要原因在于神经网络训练易于局部最优,而且基于经验风险最小的训练易于出现训练误差小,预测误差大的过学习问题。LS-SVM采用结构风险最小化原则,折中考虑经验风险和置信区间,达到实际风险最小。小波包与LS-SVM方法的预测精度优于RBF神经网络和标准LSSVM的预测精度,相关系数更趋近于1，从而说明该方法泛化能力较强,预测效果较好,不仅能充分拟合低频信息,而且可避免对高频信息的过拟合。

3 结论

石油价格的预测需要解决如何在随机性和不确定性的变化中找出规律，建立预测模型，提高预测精度，为决策者提供有效的决策依据。石油价格时序中的趋势项和随机干扰项具有不同的变化特性，因而将其分解为多个时间序列信号，并分别进行预测，有利于提高预测精度。本文结合小波包变换和最小二乘支持向量机,建立了一种新的石油价格预测模型,在充分吸取了各个单一预测模型优点的同时,利用贝叶斯推断优化了LS-SVM参数的选取。对NYMEX原油期货价格预测进行了实例验证。结果表明，相对于RBF神经网络以及标准最小二乘支持向量机预测方法，本文提出的方法很好的改善了预测精度和泛化能力，具有良好的应用前景。

[1]Suykens J.A.K.,Vandewalle.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3).

[2]SuykensJ.A.K.,VanGestelT.,deMoorB.,etal.LeastSquares Support Vector Machines[M].Singapore:World Scientific,2002.

[3]张德丰.MATLAB小波分析[M].北京：机械工业出版社，2009.

[4]Wu Hai-shan,Chang Xiao-ling.Power Load Forecasting with Least Squares Support Vector Machines and Chaos Theory[C].//Proc of Intelligent Control and Automation，2006.

[5]刘立霞，马军海.基于LS-SVM的石油期货价格预测研究[J].计算机工程与应用，2008，44（32）.

[6]Suykens J.,Gestel T.,Brabanter J.D.,et al.Financial Time Series Prediction Using Least Squares Support Vector Machines within the Evidence Framework[J].IEEE Transactions on Neural Network, 2001,12(4).

[7]陈磊,张土乔.基于贝叶斯最小二乘支持向量机的时用水量预测模型[J].天津大学学报,2006,39(9).

[8]Kwok J.T.The Evidence Framework Applied to Support Vector Machines[J].IEEE Transactions on Neural Network,2000,11(5).

[9]李方方,赵英凯,颜昕.基于Matlab的最小二乘支持向量机的工具箱及其应用[J].计算机应用,2006,26(12).

（责任编辑/易永生）

F224;F416.22

A

1002－6487（2011）06－0162-03

王欣冉(1986－)，男，吉林人，硕士研究生，研究方向：数学模型与分析。