基于情绪心理偏差的证券投资组合行为风险溢价模型

许玲艳

（湖南涉外经济学院商学部，长沙410205）

基于情绪心理偏差的证券投资组合行为风险溢价模型

许玲艳

（湖南涉外经济学院商学部，长沙410205）

文章把情绪心理偏好融入到随机折现因子与风险溢价中，对数折现因子可分解为基本成分与情绪成分之和；任何证券的期望回报率可以表示为基本溢价与一个反映情绪为基础的风险情绪溢价之和。利用这个行为风险溢价定价模式从而可以解释权益溢价、波动率之谜。

情绪心理偏差；证券投资组合；行为风险溢价

0 引言

行为金融学是行为理论与金融分析相结合的研究方法与理论体系。它分析人的心理、行为以及情绪对人的金融决策、金融产品的价格以及金融市场发展趋势的影响。行为金融学通过借鉴心理学的研究方法、吸取心理学研究成果而解释了传统金融理论不能解释的金融现象，这种学科的结合不仅完善了金融学理论体系，也从另一个角度对心理学理论进行了验证，为其应用开辟了一条新的通道。行为金融学并不能代替传统金融学，也并未贬低传统金融分析工具的价值，相反，作为对传统金融工具的补充，行为金融学帮助人们了解“投资者心理偏差”是如何影响自己和他人的投资行为的，从而尽可能有效地规避风险，保证金融市场的健康运行。其中考虑了情绪心理偏差的行为金融定价就可以利用行为贝塔、行为B-S公式、行为均值方差边界及行为利率期限结构来解释金融市场上的利率之谜、权益溢价、背离利率期限结构假说、波动率之谜。

1 情绪心理偏好影响投资组合与证券回报率

早期阿罗－德布鲁完全竞争的一般均衡思想被运用到金融学资本资产定价中。夏普把金融市场上参与者都假定马克维茨所描述的均值——方差最优化者、参与者对资产的概率分布结构的看法一致、任何参与者有且仅有一个借贷的无风险利率、无交易成本，在以上假定下获得奠定资本资产定价模型（CAPM）的市场组合理论。具体形式如下：为了获得CAPM首先界定了CML：

然后夏普市场通过构造一个有效资产组合的系统性风险解决了无效资产组合与某个独立证券资产不存在的关系。Xi为资本市场参与者投资于资产组合i的比例，XM为资本市场整个资产组合的比例，且具有以下关系：

两种构成的资产组合的预期收益率与方差为:

通过估算CML的斜率可以获得有效组合在资本市场上的方程：

对方程（6）进行恒等变形可获得CAPM模型：

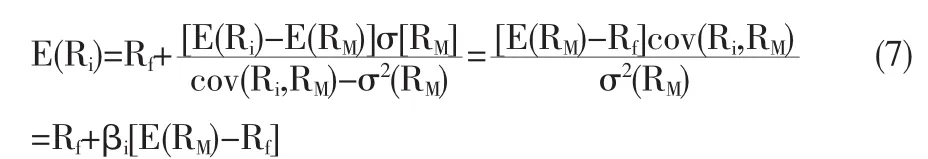
在CAPM中由于假定了参与者完全理性，否定了资本市场参与者不会面临不确定性，而且参与者可以估计出可能发生的事件及其概，从而把结果不确定性转化为可计算的风险，并具体利用方差来刻画，从而需求给定风险下的最大收益组合。坎贝尔（2003）认为不确定性在资产定价研究中起到了关键作用，以上CAPM背离了奥地利学派与奈特等人所强调的不确定性与风险差异，Campbell（2000）认为即使存在不确定性，资本市场上的投资者所需做的仅仅是确定随机贴现因子（SDF）。资本市场上的投资者面对未来，核心是平滑金融产品风险与收益，若资本市场上的投资者可以估算金融产品未来的现金流，那就可以通过SDF来估算这些金融产品的定价。在夏普的投资组合中很少考虑到金融资产以外的因素，直到Merton、Lucas、Breeden等提出了消费资本资产定价模型（CCAPM），该模型引入了参与者的效用函数使用参与者的相对风险规避系数来刻画投资者行为，获得消费贝塔系数。Breeden指出在资本市场跨期条件中，金融市场上参与者的偏好必须由消费效用函数形状来说明：若资本市场上投资机会不确定，那么对财富而言不是经常正确的。这表明资本市场上的投资组合是由投资组合对资本市场上未来消费的边际贡献来定价的，从而获得了消费资本资产定价的消费贝塔系数：

消费贝塔系数为βiC=σiC/σ2C，度量投资组合中证券收益率变动相对于总消费变动的敏感度，这样就把市场参与者的消费不确定性引入了资本资产定价中。但CCAPM无法解释Weil（1989）提出的无风险利率之谜、Mehra&Prescott（1985）提出的股票溢价之谜，存在缺陷。这时因为资本市场上参与者的同质假定导致了CCAPM虽然引入了消费效用函数，但无法刻画资本市场上参与者的行为。这种对行为的简单处理，是的定价模型中行为基础被忽视了，这样就把竞争市场均衡时主观因子SDF变成了与事实相一致的客观因子。在行为资本资产定价模型为了寻找SDF新的决定因子，就必须引入诸如习惯形成、财富偏好、损失厌恶、追赶时髦、嫉妒、偏好异质、类型异质等各种异质假定。这种思想导致了资本市场参与者效用函数的修正，并在卡尼曼发展的行为经济学基础上考虑SDF行为层面，以此来实现更为精确的SDF刻画。而在SDF引入情绪心理偏好就是其中一个发展方向。

投资者情绪理论最早由Lee、Shleifor&Thaler提出了，Lee、Shleifor&Thaler认为封闭式基金的持有者中有一些是噪音交易者，噪音交易者对未来收益的预期很容易受到不可预测的变动的影响。当噪音交易者对收益持乐观态度时，基金的交易价格就会上涨，出现相对于基金资产净值的溢价；当噪音交易者对收益持悲观态度时，基金的交易价格就会下跌，出现折价。所以，持有封闭式基金就有两部分风险：基金资产价值的波动风险和噪音交易者情绪的波动风险，投资者持有封闭式基金比持有基金投资组合的风险更大。若噪音交易者风险具有系统性，那么理性投资者就会要求对此进行补偿。封闭式基金的市场价格应低于其投资组合的资产净值，由此产生了封闭式基金的长期折价交易现象。在中国资本市场上，封闭式基金折价率以及认购权证隐含波动率间接反映中国证券市场的投资者情绪，并将一定程度反映中国证券市场投资者情绪与市场行情之间的关系：（1）封闭式基金折价率可以间接反映机构投资者情绪，基金折价率越高，表明机构投资者越看淡市场行情，对市场走势持悲观态度；认购权证隐含波动率可以间接反映个人投资者情绪，隐含波动率越低，表明个人投资者越看好市场行情，对市场走势持乐观态度。（2）用封闭式基金折价率反映机构投资者情绪时，机构投资者情绪显著影响市场收益率，投资者情绪越高涨，市场指数收益率越高；机构投资者情绪也显著影响市场收益的波动性，并通过收益波动再次对市场收益产生风险溢价，表明机构投资者情绪是影响市场收益的系统性因素；机构投资者情绪对未来市场收益与市场收益的波动性均有较强的预测能力。（3）利用认购权证隐含波动率反映个人投资者情绪时，个人投资者情绪变化显著影响市场收益率，投资者情绪变得越高涨，市场指数收益率越高；个人投资者情绪变化也显著影响市场收益的波动性，表明个人投资者情绪变化是影响市场收益的系统性因素；个人投资者情绪变化对未来市场收益与市场收益的波动性也均有较强的预测能力。

2 基于情绪心理偏差的投资组合回报率行为定价模型

2.1 考虑情绪心理偏差的投资组合回报率行为定价思路

对于资本市场参与者偏好除了用效用函数描述外，还有主观贴现因子，它反映了资本市场参与者对未来效用的评价。新古典经济学中一般假定主观贴现因子小于1，而Kocherlakota在1990年突破了该金科玉律，证明了主观贴现因子可以大于1，在一定程度上可以缓解股票溢价之谜与无风险利率之谜。Becker&Mulligan在1997年构建了主观贴现因子内生决定的理论模型；Mehra&Sah在2002年把主观贴现因子的波动称为情绪波动，并阐述了改主观贴现因子对均衡股票回报率的定量影响。从以上研究看为了获得考虑情绪心理偏差的行为投资组合定价模型，必须改变金融资产定价理论中处于核心地位的随机折现因子，通过融入行为金融的思想把改随机折现因子变为行为随机折现因子，这样就可以创造出与传统金融资产定价理论相对称的核心行为要素。从构建的过程来看，考虑了情绪心理偏差的行为随机折现因子具有不同的函数表达式：若资本市场上所有投资者情绪心理偏好都是积极的，那行为随机折现因子就是向上倾斜的；若资本市场上所有投资者情绪心理偏好都是消极的，那行为随机折现因子就是向下倾斜的；若部分投资者情绪心理偏好都是积极的、部分投资者情绪心理偏好都是消极的，那行为随机折现因子就是震荡为特征的形状。这样在考虑了情绪心理偏好的资本资本定价模型中，对数行为随机折现因子就可以分解为基本成分与一个情绪心理偏好成分两部分。若投资者情绪心理偏好存在，资本资产定价模型与不存在情绪心理偏好的定价模型不同，这种融入情绪心理偏好的行为随机折现因子给资产价格带来了额外的波动率，影响了收益率曲线的斜率。

2.2 考虑情绪心理偏差的投资组合回报率行为定价

任何证券Z的风险溢价由回报率与随机折现因子之间的协方差来确定：

其中，r(Z)表示证券的总回报率向量，M为定价核，单位概率的定价状态，而且有：

利用期望及方差的不等式并令X是Mt+1而Y是rt+1(Z)-rt+1(F)，就有：

给定情绪心理偏差：

其中Φ反映投资者偏差导致的偏离：来自投资者信念与客观信念的差异；来自投资者均衡时间折现因子与所有投资者客观信念时的均衡时间折现因子的差异，具体给出：

这样就可以获得对数折现因子的表达式：

方程（14）表明对数折现因子可以分为两个随机过程之和：情绪过程与总消费增长为基础的过程。现在把这种结构拓展到人任何证券的风险溢价的形式。

为了给出行为风险溢价，对于欧拉方程t=0与t=1的相关回报率分布为rZ的Z有：

对于一般的γi来说，对于方程（15）边际效用比率可以用以下形式来替换：cj(x0)/cj(x1)，因此可以得到：

欧拉方程对于资本市场上的单个投资者来说是成立的，这时投资者对投资组合的均衡选择是整个组合。所以，给定J=R就可获得以下方程：

按照Φ的界定，PR=(δΠ/δR)Π准。在欧拉方程中利用以上式子替换可以得到：

对hz,0进行界定：

可以推出：

这样就可以得到：

利用期望及方差的不等式及Ghysels&Juergens(2004)的公式，可以导出：

对该方程进行重新排列：

利用方程（6）替换EΠ,0[g(xt)-γRrz(x1)]，可以化简：

随机折现因子的期望值等于无风险证券的价格，即Et(Mt+1)=1/i1；若证券的价格有效就有：Et(Mt+1)=1/i1,Π=δΠEΠ(g(xt))-γR。根据方程（22）与（23）可以得到：

其中rb,1=i1,Π/hZ,0，这样推出i1,Π=rb,1hZ,0，所以方程（24）变为：

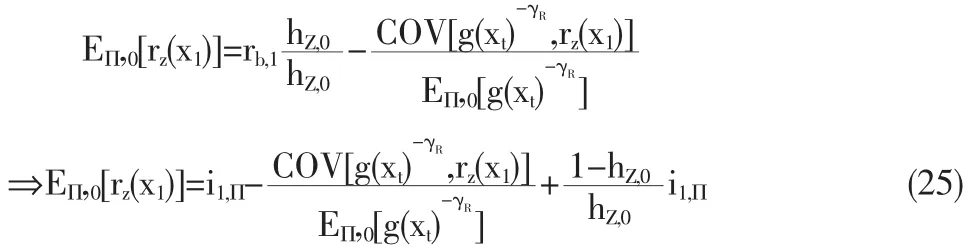
在方程（25）中可以看出证券Z的真实风险溢价受到情绪心理偏差的影响。这样任何证券风险溢价的标准形式变为：

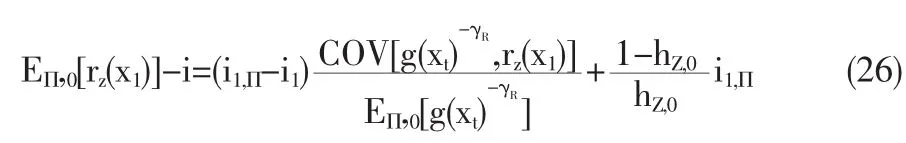
从方程（26）的右边可以看出，任何证券Z的期望回报率又三个部分组成：价格有效时出现的利率（均衡利率错误定价的程度）；基本风险溢价；情绪溢价（与证券回报率自身错误定价程度相关的溢价）。

在以上方程中Φ中变量PR/Π的作用是在g(x1)-γR,rz(x1)变量中赋予乘积g(x1)-γR，rz(x1)新的权重。若在时间t，代表资本市场上投资者在t+1时对证券Z的回报率过分乐观，那在t+1时g(x1)-γR,rz(x1)高实现值的事件xt+1就会在EΠ,0[δΠ准g(x1)-γRrz(x1)]中比在EΠ,0[δΠg(x1)-γRrz(x1)]得到更多的重视，这时就会有hZ,0≥1。从而表明证券Z在时期t的定价偏高，这时会看到情绪心理偏差的溢价成分就会为负数，即定价偏高的证券组合具有异常的期望回报率为负的特征，这点也是符合资本市场上投资者的直觉的。

3 结论

情绪的心理偏差如何体现在资本资产定价的随机折现因子与风险溢价中，通过以上方程给出两个重要结论：资本资产定价的随机折现因子可以分解为一个基本成分与情绪心理偏差之和；任何像股票、权证、基金的证券期望回报率也可以表示为一个对应有效价格的基本溢价与一个反映以情绪心理偏差为基础的风险情绪心理偏差之和。在股票、权证、基金等证券价格有效时，情绪心理偏差为零，此时随机折现因子就为基本溢价，同时风险溢价则反映其基本风险。

[1]安德瑞·史莱佛，并非有效的市场——行为金融学导论[M].北京：中国人民大学出版社，2003.

[2]Abel,Andrew B.Asset Prices Under Habit Formation and Catching Up with the Joneses[J].American Economic Review Papers and Proceedings,1990,1(80).

[3]Barberis,Nicholas,Ming Huang,Tano Santos.Prospect Theory and Asset Prices[J].Quarterly Journal of Economics,2001，116（1）.

[4]Boldrin,Michele,LawrenceJ.Christiano,JonasD.M.Fisher, Habit Persistence and Asset Returns in an Exchange Economy[J]. Macroeconomic Dynamics,1997，（1）.

[5]Campbell,John Y.,John H.Cochrane,Explain the Poor Performane of Consumption-based Asset Pricing Models[J].Jounal of Finance,2000，（6）.

（责任编辑/亦民）

F830.9

A

1002－6487（2011）06－0138-03

许玲艳（1981-），女，湖南衡阳人，硕士，讲师，研究方向：财务会计理论与实务。