端面对轴线的垂直度误差测量及评定的新方法*
2011-10-18林志熙黄富贵
林志熙 黄富贵
(①福建工程学院机电及自动化工程系,福建福州350108;②华侨大学机电系,福建泉州362021)
检验端面对轴线垂直度误差的传统方法,一般将基准轴线调至与平板垂直,用指示计在整个被测表面上测量,并取指示计的最大读数差作为被测端面对基准轴线的垂直度误差。这种检测方法不符合GB/T 1958—2004规定中端面对轴线垂直度误差的定义,只能用于检验位置精度要求较低的零件,且调整、测量效率低。
如何应用简单方便但又符合国家标准定义的方法来测量和评定面对线垂直度误差,一直是该领域研究人员的研究热点之一。文献[1]用万能工具显微镜测量,介绍了端面对轴线垂直度误差最小二乘评定法,测量设备成本较高,且不符合形位误差国家标准的定义。针对这一问题,本文采用光学分度头测量,建立基准符合最小条件法、最小二乘法、端点连线法的面对线垂直度误差的数学模型,基于该模型研发了计算机数据处理系统,该系统既能求出基准轴线的空间任意方向直线度误差,还能求出端面对轴线垂直度误差,并绘出直观形象的三维模拟图形。该方法符合垂直度误差国家标准的定义,且测量方便,数据处理效率高。
1 数学模型
在评定端面对轴线垂直度误差时,首先要确定基准要素的方向,即对空间任意方向直线度误差进行评定。然后垂直于基准要素方向,对被测平面作两个最小包容平行平面,此平行平面即形成被测要素最小包容区域,该平行平面间距离,即为被测要素在给定方向上相对基准要素的垂直度误差。
1.1 建立基准轴线
基准轴线的建立,即对空间任意方向上直线度误差的测量与评定。形状和位置误差检测国家标准GB/T 1958—2004中提出的“最小条件原则”,即评定时被测提取要素对其拟合要素的最大变动量为最小[2]。如图1所示。首先是对被测孔或轴的不同横截面圆进行测量采点,按最小条件法拟合出各横截面圆的拟合圆心C,连接这些圆心即得到空间提取轴线2,包容提取空间轴线上的各测点、且直径最小的最小包容圆柱面4的直径就是被测实际孔心线或轴心线的直线度误差,该圆柱体的轴线1即为基准轴线。
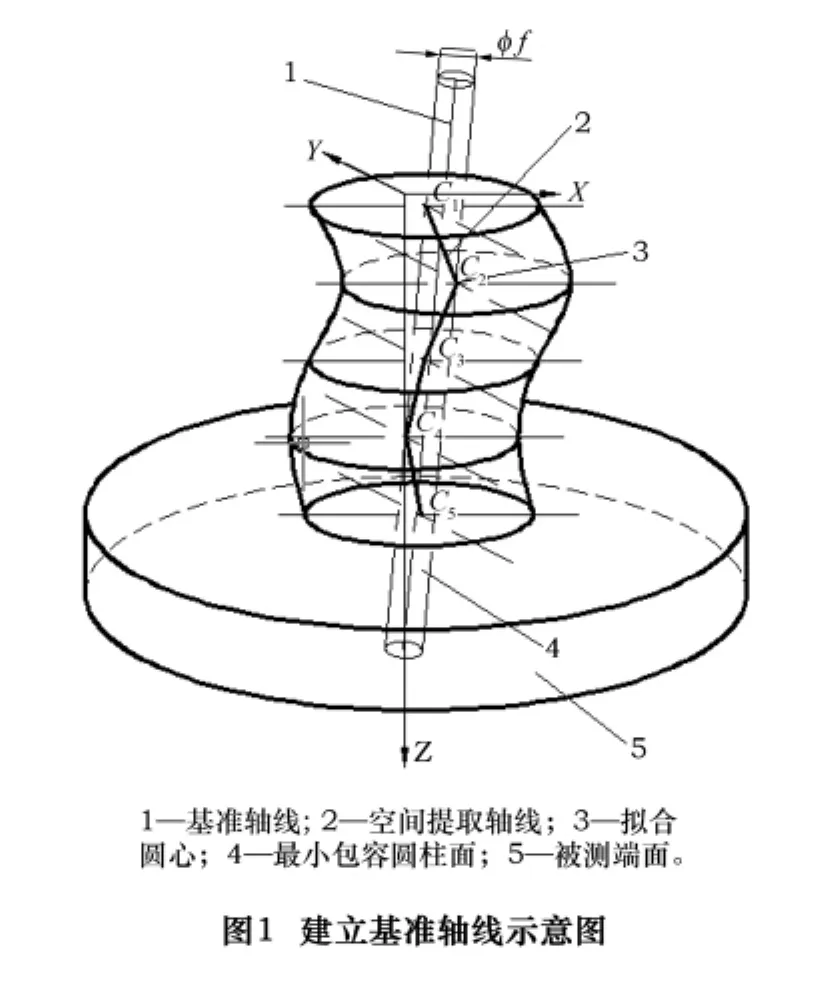
1.1.1 空间提取轴线的确定
对被测孔或轴的不同横截面圆进行等角度间隔采样,如图2中所示,在某一截面各采样点分布。O为分度头回转中心,即坐标原点,Δri为该截面测得的半径变化量,θi为各被测点的回转角(i=1,2,…,n)。因此测点直角坐标值 xi=(r0+ Δri)cosθi,yi=(r0+ Δri)sinθi。其中r0为基圆半径(这是个未知数,但接近零件的基本尺寸)。
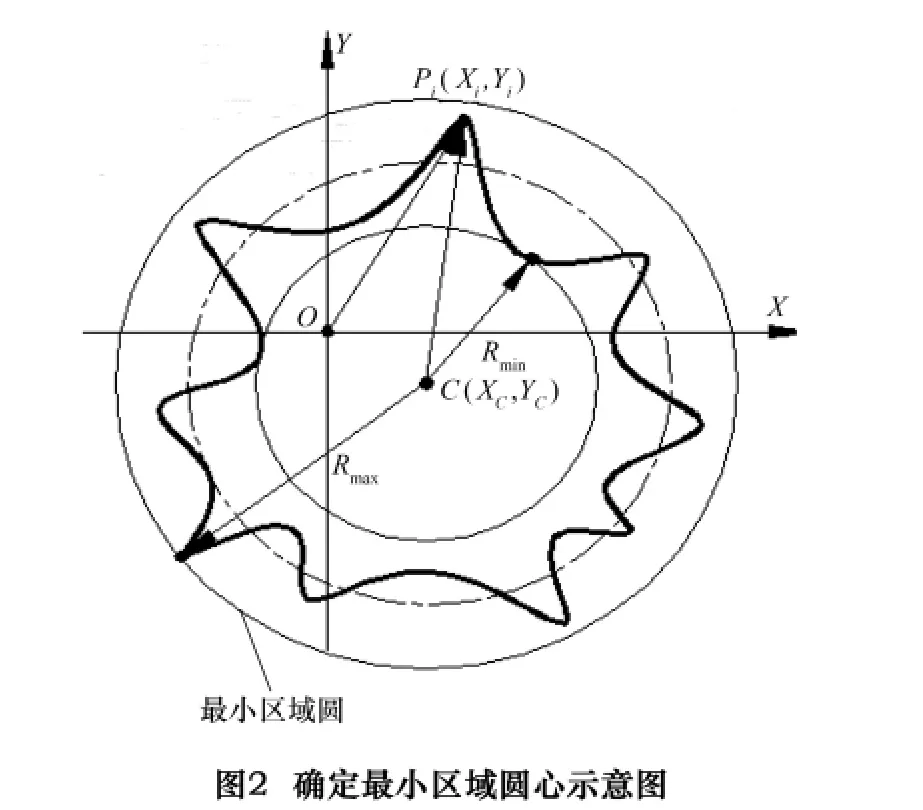


满足最小化时,F(x,y)的(x,y)即为各采样截面内实际轮廓的符合最小条件的拟合圆心。基准提取轴线就由各拟合圆心C1,C2,…,Cn连成的空间折线来体现,如图1所示。
1.1.2 空间任意方向直线度误差的评定和基准方向的确定
在空间任意方向评定直线度误差时,常用最小条件法、最小二乘法、两端点连线法。其中按最小包容区域法评定符合公差带概念,求得的误差值最小,一般作为争议时的仲裁依据。
设拟合基准轴线L为

方向由 j、k、q 三个参数决定,位置由 u、v、g 决定。各拟合圆心点C(xi,yi,zi)到拟合基准轴线的距离为
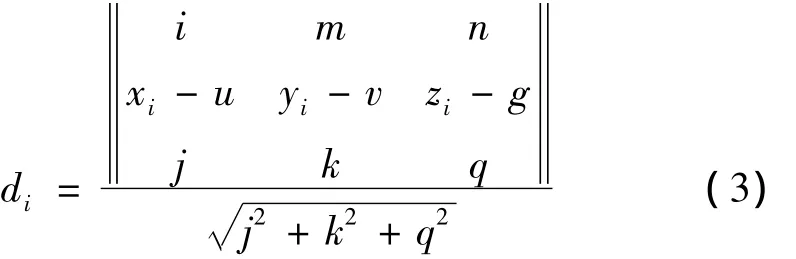
(1)最小条件法
按最小区域法评定直线度误差实质上是寻找最小外包容圆柱,则其目标函数定义为 F(u,v,g,j,k,q)={max(di)},满足最小化时,F(u,v,g,j,k,q)的(u,v,g,j,k,q)即为理想空间轴线 L,且该六元函数 F(u,v,g,j,k,q)的最小值的两倍即为空间任意方向直线度误差。
(2)最小二乘法
根据最小二乘原理,找到最小二乘中线即拟合基准轴线L,使拟合圆心到该直线的距离平方和为最小。即目标函数 F(u,v,g,j,k,q)={∑d2i}满足最小化。最小二乘中线的最小包容圆柱面的直径即为空间任意方向直线度误差。
(3)端点连线法
拟合基准轴线L与两端点连线平行(或重合),并具有最小直径的两端点连线包容圆柱面。两端点坐标已知,分别为(x1,y1,z1)和(xn,yn,zn),因此拟合基准轴线方向向量为
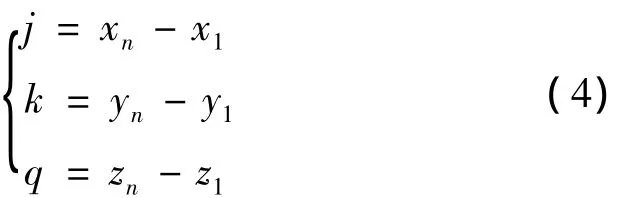
其目标函数F(u,v,g)={max(di)}满足最小化时,即可求得空间任意方向直线度误差及拟合基准轴线L。
1.2 评定垂直度误差
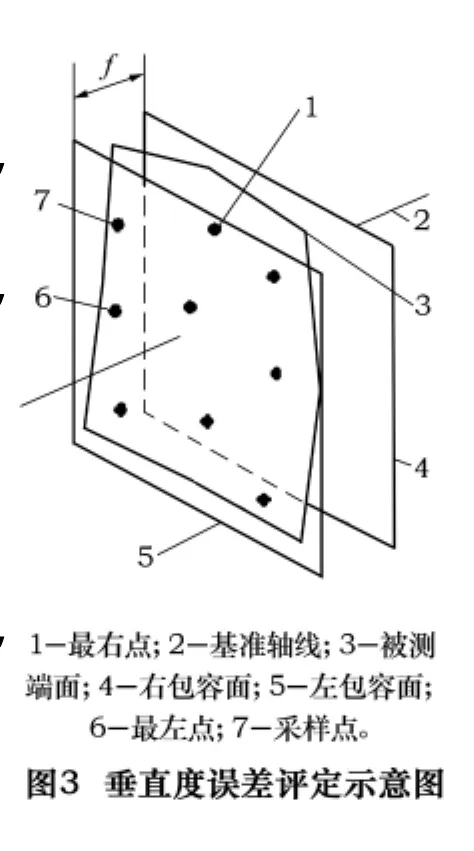
拟合基准轴线确定后,就可进一步计算被测端面对基准轴线的垂直度误差。根据定义,定向最小区域是指按拟合要素的方向包容被测提取要素时,具有最小宽度f或直径Φf的包容区域[2]。包容被测提取端面、垂直于拟合基准轴线并且相距最近的两平行平面间的距离,即为端面对轴线的垂直度误差值。

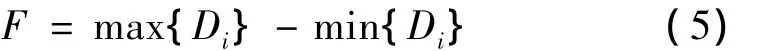
2 Matlab程序设计
最小区域圆心的确定,用最小条件法、最小二乘法、端点连线法,评定空间任意方向直线度误差和基准方向,分别属于求解二元、六元、三元函数在指定点附近最小值,即求解无约束条件非线性极小值。Matlab 7的优化工具箱中的优化算法函数 fminsearch和Fminunc均可解决此类问题。只要建立以上所述的目标函数,调用相应的函数,即可求得结果,无需编写求解的程序,求解过程非常简单。而评定垂直度误差运用Matlab数值计算功能,通过正确的数学模型即可得[3-5]。
笔者还设计了可供用户方便操作的图形用户界面[6-7],用户可直接在界面上将所测得的数据输入到相应的文本框中,选定方法,即可得到基准要素3种评定方法的空间任意方向直线度误差以及垂直度误差评定结果。利用Matlab强大的图形功能对实际被测平面进行三维显示[3-5]。绘制出基准要素3种评定方法确定的基准理想要素,被测要素的实际轮廓即折面图和上、下包容面,并可将该图进行旋转、缩放,可清楚地反映出被测量的几何特征及评定准则的应用情况,对计算结果进行验证。该软件计算精度高,直观明了,实用性强。
3 测量实例

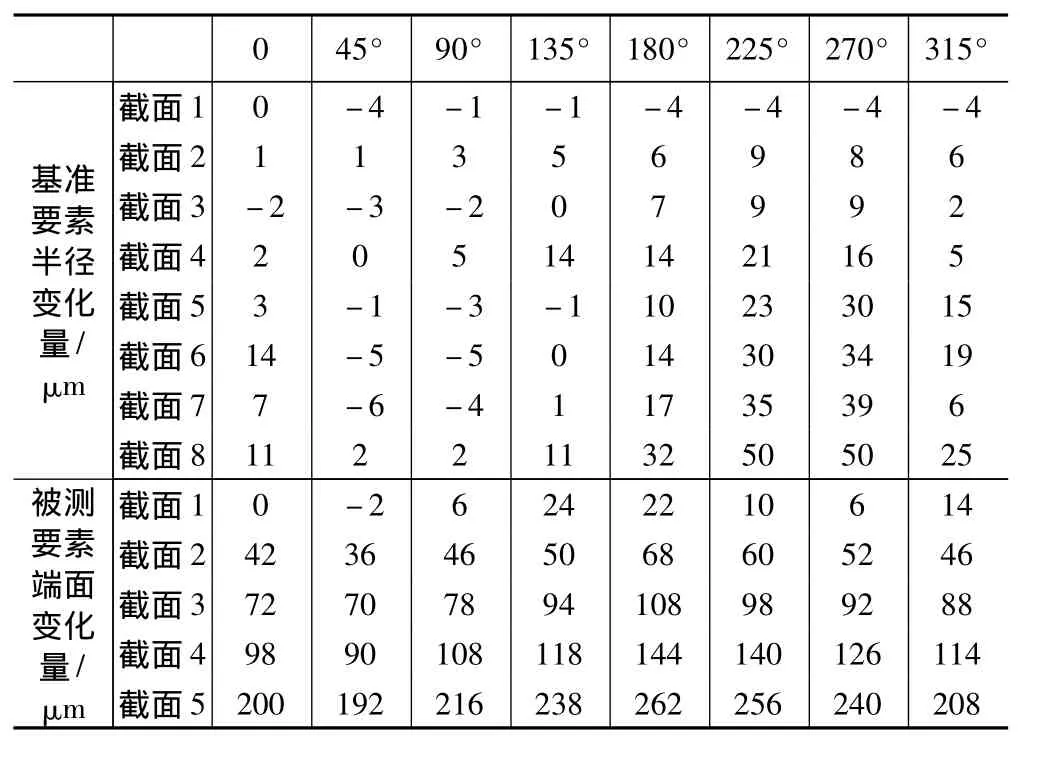
表1 测量数据
用光学分度头对一工件(如图4所示)进行实际测量。在工件圆柱上相邻15 mm截取8个截面,每个截面每转过45°由指示表在被测轮廓上测取相应的半径变化量△r。在光学分度工作台上加装一垂直导向定位块,移动杠杆千分表,在工件端面上从圆心开始向外每10 mm测量端面变化量,共测量5个截面,每截面测量间隔也为45°。所测数据如表1所示。
将测量数据输入系统界面,选择基准要素的评定方法,可分别计算直线度及垂直度误差。并在界面左边绘出误差示意图,进一步验证算法的正确性。如图5所示。

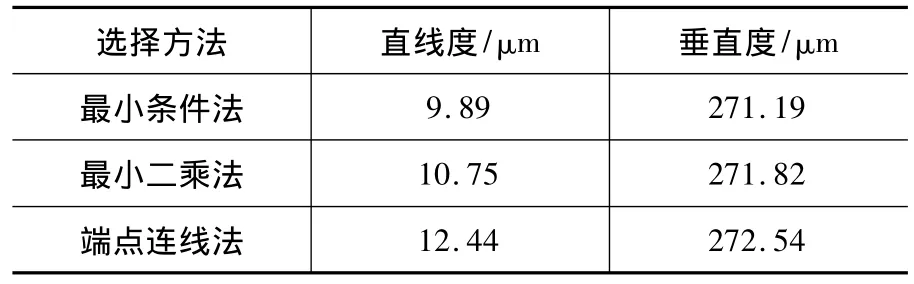
表2 测量结果
最小条件法、最小二乘法、端点连线法等3种数据处理方法所得的结果见表2。其中最小条件法求出的基准轴线直线度误差值最小,符合国标规定,而垂直度误差由被测平面决定。
4 结语
(1)本文介绍的基准符合最小条件法、最小二乘法、端点连线法的面对线垂直度误差的评定方法,具有数学模型简单、编程容易、程序短和运行速度快等特点。
(2)该系统可同时满足符合最小包容条件的基准轴线空间直线度误差和端面对轴线垂直度误差的求解。
(3)检测示意图清楚地反映出被测量的几何特征及评定准则的应用情况,对计算结论进行验证。
(4)通过测量实例,证明了这种测量及评定方法准确度高、处理效率高、成本低、适用范围广、实用性强;具有较高的理论价值和实用价值,是一种较好的计算机辅助形位误差评定系统。
[1]甘永立.几何量公差与检测[M].上海:上海科学技术出版社,2004.
[2]中华人民共和国国家标准GB/T 1958—2004:产品几何量技术规范(GPS)形状和位置公差检测规定[S].北京:中国标准出版社,2005.
[3]张志涌.精通 MATLAB 6.5版[M].北京:航空航天大学出版社,2003.
[4]飞思科技产品开发中心.MATLAB 7基础与提高[M].北京:电子工业出版社,2005.
[5]Gerald Recktenwald.数值方法和MATLAB实现与应用[M].伍卫国,方群,张辉,等译.北京:机械工业出版社,2004.
[6]王默玉,宗伟,刘春磊,等.基于MATLAB的图形用户界面的构造方式与应用[J].现代电力.2002.19(1):76-78.
[7]梁辉.MATLAB制作图形用户界面的应用[J].佳木斯大学学报,2003,21(4):403-407.
