基于MPI的二维泊松方程差分并行实现与测试

苑 野，杨东华

(哈尔滨工业大学基础与交叉科学研究院，哈尔滨150080)

随着高速网络和多核处理器技术的发展，集群系统获得了很好的性能.由于性价比高和可扩展性好的特点，集群正逐渐成为主流的并行平台.MPI(Message Passing Interface)消息传递是一种典型的并行编程模型.由于集群是一种典型的分布式存储系统，因此MPI消息传递系统已经成为目前集群上最重要的并行编程环境之一.

在科学计算中经常要数值求解各类偏微分方程.Poisson方程广泛应用于电学、磁学、力学、热学等多个领域，因此解决Poisson方程的计算问题成为了高性能计算领域中的一个最基本问题.目前比较常用的方法有有限差分法、有限元法和有限体积法.用差分方法解Poisson方程，解的结果就是方程的准确解函数在节点上的近似解，这种方法主要是集中在依赖于时间的问题.与其他两种方法相比，有限差分法简单，易并行.因此我们用有限差分方法求解Poisson方程.本文抛开复杂的理论问题，在高性能集群环境下，针对矩形区域上二维Poisson方程边值问题的五点差分格式，使用雅可比迭代法和MPI消息传递接口模型对一类简单的Poisson方程给出了其差分方程组的并行实现解法，并定量的对该类解法的并行化性能进行了测试.

1 MPI技术

消息传递是一种广泛应用的并行编程模型.MPI(Message Passing Interface)是1994年5月发布的一种消息

传递接口，它定义了用C和Fortran编写消息传递应用程序所用到的核心库例程的语法和语义，具有很多特点.首先，MPI提供了一个易移植的编程接口和一个可靠的通信接口，允许避免内存到内存的拷贝，允许通信重叠，具有良好的通讯性能;其次，它可以在异构系统中透明使用，即能在不同体系结构的处理器上运行;再者，MPI提供的接口与现存消息传递系统接口(如PVM、NX等)相差不大，却提供了更大的灵活性，能在更多的平台上运行;最后，MPI是一个标准，它没有规定底层必须如何实现，故给实现该标准的厂家带来了更大的灵活性，使MPI可扩展性更好.

1.1 最基本的MPI

MPI是个复杂的系统，它包含128个函数(1994年标准)，1997年修订的标准MPI-2已经超过200个，目前常用的大约有30个，然后使用其中的6个最基本的函数就能编写一个完整的MPI程序，6个函数如下.

MPI_INT MPI 初始化MPI_FINALIZE结束MPI计算MPI_COMM_SIZE确定进程数MPI_COMM_RANK确定当前进程标识MPI_SEND发一条消息MPI_RECV 接受一条消息

1.2 组通讯

MPI提供了强大的组通讯功能，可以满足进程间的组通信.组通信一般实现3个功能:通讯、同步和计算.通讯功能主要完成组内数据的传输，分为3种，即一对多通讯，多对一通讯和多对多通讯;而同步功能实现组内所有进程在特定的地点在执行进度上取得一致;计算的功能比较复杂，要对给定数据完成一定的操作.组内通信函数主要包括5类:同步(Barrier)、广播(Bcast)、收集(Gather)、散发(Scatter)和规约(Reduce).

1.3 通信体

通信体是由一个进程组和进程活动环境(上下文)组成.其中进程组就是一组有限和有序进程的组合;进程活动环境是系统指定的超级标记，它能安全地将相互冲突的通信区分开.通信体提供了MPI中独立的安全的消息传递，不同的通信库使用独立的通信体，保证了在同一通信体的通信操作互不干扰.

2 Poisson方程简介

2.1 Poisson方程的定义

Poisson方程是数学中的一种偏微分方程，即为

其中:Δ代表的是拉普拉斯算子，而f和Δ可以是在流形上的实数或复数值的方程.当流形属于欧氏空间，而拉普拉斯算子通常表示为▽2，因此Poisson方程通常写成

在二维直角坐标系统中，Poisson方程可以写成

2.2 二维Poisson方程的差分离散

考虑区域Ω=(0，a)×(0，b)上的Poisson方程的第一边值问题

将Ω沿着x，y轴方向均剖分为m，n等分，沿x方向上的步长记为，沿y方向上的步长记为，剖分节点记为(x，y)(i=1，…，m-1，j=ii1，…，n-1).用 μij表示 μ 在节点(xi，yi)的差分近似解，则离散后的差分方程为

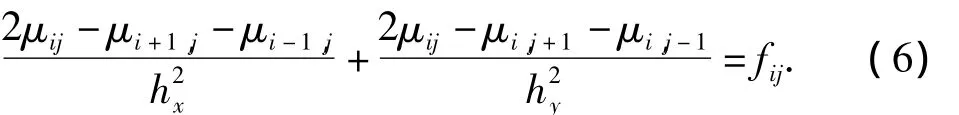
对于格式(3)～(7)，可以使用各种迭代法求解，常用的有逐次超松弛迭代法、共轭梯度法、预条件共轭梯度法、交替方法及多重网格方法等，其中雅可比迭代法以其简单实用和易于并行实现一直受到人们的重视.格式(3)～(8)的雅可比迭代格式为

3 实例数据测试与结果分析

表1 题规模及串行程序执行时间

表2为所测试问题的规模及多处理机程序执行时间.对并行算法的性能测试主要是通过加速比和并行效率.我们以问题的多处理机执行时间与单处理机系统执行时间的比值作为多机加速比，把并行算法的加速比与CPU个数之间的比值定义为并行效率.图1为不同问题规模下的多机并行加速比.图2为不同问题规模下的并行效率.

表2 不同问题规模下多处理机程序执行时间

由图1可知，当矩阵为400阶时，问题的规模较小，随着节点数目的增多，加速比持续下降，且在节点数node=4时，获得最大加速比为1.16;当矩阵为800阶时，问题规模比较大时，其加速比均大于1，且几乎成线性增长;当矩阵为1 600阶时，问题规模较大，其加速比随节点的增加，表现为先逐渐变大，然后迅速减小.当node=9时，获得最大加速比为2.9655，且node=16时的加速比大于node=4时的加速比，但由图2可知其并行效率下降了61.6%，可以预测，当节点数继续增加时，其加速比和并行效率将会持续降低.由图2可知，当问题规模比较小时，矩阵规模小于800阶，随着节点数的增加，并行效率逐渐降低，但问题规模越大其并行效率也越高.

4 结语

通过上述实验数据可知，此类Poisson方程的并行效率和加速比很难得到非常理想的值，主要原因在于:问题规模的大小，如果问题规模较小(如:矩阵为400阶或800阶)，并行计算的任务量较小，几个处理器就足够了，若处理器太多，则难以实现最佳负载平衡同时处理器也得不到充分利用.反之，如果问题规模较大(如:矩阵为1 600阶)，则需要更多的处理器.但随着处理器个数的增加，并行算法的加速比在峰值后呈现下降趋势，并行效率也在下降.

[1]陈国良.并行计算—结构·算法·编程(修订版)[M].北京:高等教育出版社，2003.

[2]王同科，谷同祥.Poisson方程差分格式的SOR方法中最优松弛因子的回归分析方法[J].工程数学学报，2005，22(3):474-480.

[3]陆金莆，关 治.偏微分方程的数值解法[M].北京:清华大学出版社，2004.

[4]章隆兵，吴少刚，蔡 飞，等.PC机群上共享存储与消息传递的比较[J].软件学报，2004，15(6):842-849.

[5]胡明昌，史 岗，胡伟武，等.PC机群上JIAJIA与MPI的比较[J].软件学报，2003(7):1187-1194.

[6]张武生，薛 巍，李建江，等.MPI并行程序设计实例教程[M].北京:清华大学出版社，2009.

[7]都志辉.高性能计算并行编程技术-MPI并行程序设计[M].北京:清华大学出版社，2001.