关联规则挖掘Apriori算法的研究与改进

2011-10-17王铮周国光

网络安全技术与应用 2011年4期

王铮周国光

重庆大学计算机学院重庆 400044

0 引言

为了方便快速的从事务数据库中挖掘出频繁项集，本文依据Apriori算法的思路加以改进，将事务数据库转换成0-1矩阵，通过0-1矩阵可很快计算出各个候选集的支持度计数，省去了 Apriori算法中的连接步骤和删除步骤这样避免了传统Apriori算法频繁扫描数据库的操作，从而提高了算法的效率。

1 关联规则Apriori算法

Apriori算法是R.Agrawal和R.Srikant于1994年提出的为布尔关联规则挖掘频繁项集的原创性算法。Apriori使用一种称作逐层搜索的迭代方法，k项集用于探索(k+1)项集。首先，通过扫描数据库，累积每个项的计数，并收集满足最小支持度的项，找出频繁1项集的集合。该集合记作L1。然后L1用于找频繁2项集的集合L2，L2用于找L3，如此下去，直到不能再找到频繁k项集。找每个Lk需要一次数据库扫描。为提高频繁项集逐层产生的效率，Apriori算法利用了一个性质用于压缩搜索空间。Apriori性质:频繁项集的所有非空子集也必须是频繁的 Apriori性质在挖掘频繁项集中的应用可以用Lk-1产生Lk为例来说明，用Lk-1产生Lk包含两步，即连接步和剪枝步。

（1）连接步：由Apriori性质，频繁项集的子集一定频繁。Lk的任一项集一定是Lk-1某项集的超集。通过Lk-1内部项集间的连接，生成候选 k-项集记作Ck。如果两个项集有(k-2)个相同的项，Lk-1的元素是可连接的。

（2）剪枝步：由Apriori性质：任何非频繁的(k-1)项集都不是频繁k项集的子集。因此如果候选k项集的(k-1)项子集不在Lk-1中，则改候选也不可能是频繁的，从而从Ck中删除。

2 改进算法

2.1 Apriori算法缺陷

Apriori算法作为关联规则挖掘的经典算法，能够比较有效的产生频繁项集，但也存在几个缺陷：

（1）扫描数据库的次数太多，每次寻找k频繁项目集时都需要扫描数据库来获得候选集的支持度，共需扫描n次，如果数据库很大则算法效率太低。

（2）利用k频繁项集连接产生(k+1)候选项集，判断连接条件时重复次数太多。

2.2 Apriori算法改进

针对以上情况，产生了一种基于矩阵的改进 Apriori算法。它将矩阵的思想应用到Apriori算法中，将数据库表示成矩阵的形式。改进算法思想可描述为：成员表示行向量，事务表示列向量，若第i个成员在第j个事务中，则矩阵的第i行，第j列的值为1，否则为0，称其为数据库的布尔矩阵。求频繁k项集之前，先统计每个项目Ii在频繁k-1项集中出现的次数b，如果b小于 min_sup，则删除事务矩阵中的第Ii行。随着k值的变大，事务矩阵将变得越来越小，从而提高了算法的效率。

3 实例分析

给出的事务数据库如图1所示，设最小支持度min_sup=2，利用上述改进算法，找出频繁k-项集。

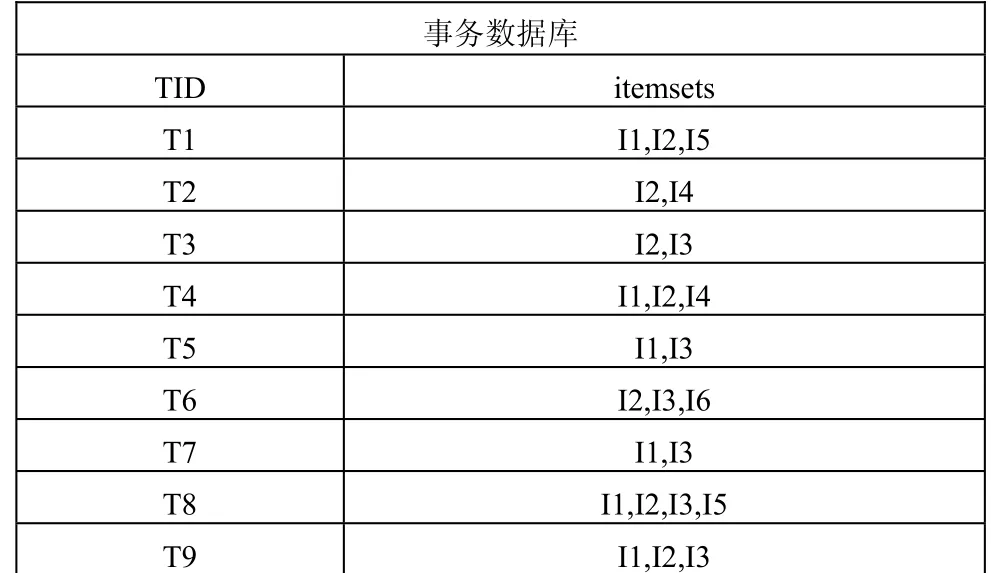
图1 事务数据库

（1）根据事务数据库构造出事务矩阵，如图2所示。

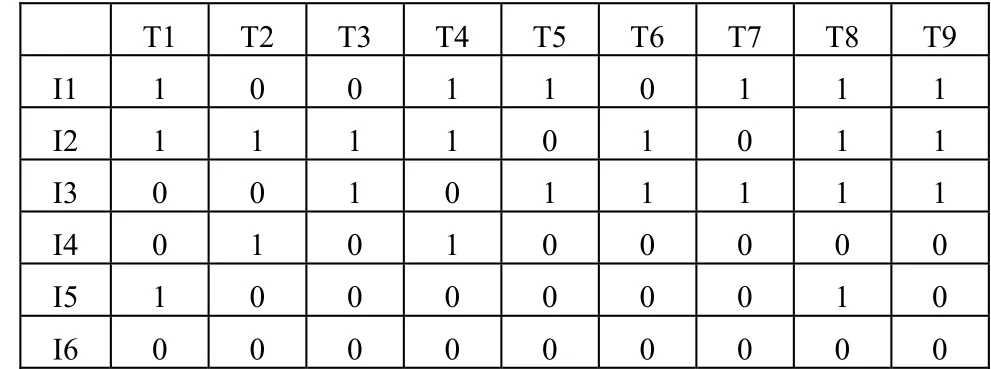
图2 将事务数据库变换为事务矩阵

（2）求频繁1项集。第i行为1的个数之和就是Ii的出现次数。从上面的矩阵可看出只有I6的次数为1小于min_sup，故矩阵变成如图3所示，得到频繁1项集 L1={I1, I2,I3, I4,I5}

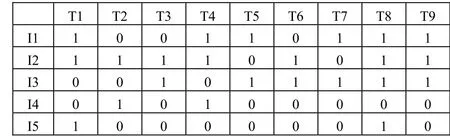
图3 修建后的矩阵

（3）k=2求频繁2项集。Ii, Ij为1就是分别计算第i行和第j行同时为1的个数和。从图2的矩阵可求出{I1,I2}=4,{I1,I3}=3,{I1,I4}=1,{I1,I5}=2,{I2,I3}=4,{I2,I4}=2,{I2,I5}=2,{I3,I4}=0,{I3,I5}=1,{I4,I5}=0。得到频繁 2项集 L2={{I1,I2 },{I1,I 3},{I1,I5 },{I2 ,I3 },{I2 ,I4 },{I2 ,I5 }}。然后统计每个项目在L2中出现的次数，可看出I4只出现了一次小于min_sup，所有删除图3矩阵的I4行(如图4)。

图4 再次修建后的矩阵

（4）k=3求频繁3项集。对图4的矩阵4个行向量取3行任意组合。连接运算有{.I1,I2,I3}{ I1,I2,I5,}{,{I1,I3,I5},I2,I3,I5}4个三项集。从图 4的矩阵中看出{I1,I2,I3}支持度计数为 2{I1,I2,I5}支持度计数为2,{I2,I3,I5}支持度计数为1，{I1,I3,I5}的支持度计数为 1。因此频繁 3项集 L2={{I1,I2 ,I 3},{I1,I2 ,I5 }，此时频繁项集的个数小于4，循环结束。