基于Excel的考试分数简易定量分析方法

刘东华，潘求丰

(江西农业大学南昌商学院，江西南昌330013)

基于Excel的考试分数简易定量分析方法

刘东华，潘求丰

(江西农业大学南昌商学院，江西南昌330013)

文章使用Excel数据分析工具对某科考试分数进行定量分析，操作简单快捷，得到了比较全面的、有价值的数据信息，便于使用数量统计的方法推断考试的总体情况，分析考试班级差异，可供教师定量评价考试分数时推广使用。

数据分析；描述统计；直方图；t检验

引言

考试试卷批改完之后，教师需要对某班的考试分数进行分析，计算平均分、最高分、最低分、标准差等描述统计量；进行频度分析，统计各个分数段的人数，得出优秀率、及格率和不及格率；分析对比两个班级的成绩差异等。将考试分数输入Excel单元格区域中，应用“数据分析工具”可以快速得到上述分析结果。下面通过例子演示Excel的分析过程。

在某科考试中，A班有20人，考试分数分布在B2:B21，B班有21人，考试分数分布在C2:C22中，如图1所示。

根据上述试卷分析目的，Excel分析任务有三项：第一项是计算出考试分数的平均值、最大值、最小值、方差等基本统计量，可以采用Excel数据分析工具中的“描述统计”功能完成；第二项是统计各分数段的人数分布情况，可以采用Excel数据分析工具中的“直方图”来完成；第三项是定量比较分析A班和B班的考试分数差异，可以采用Excel数据分析工具中的T检验、F检验完成。准备好数据后进行相应的设置，Excel能快速准确地给出相应的分析结果。下面简略介绍上述三项分析任务通过Excel分析工具库完成的过程、理论依据，以便使用者举一反三，灵活应用。

一、Excel描述统计功能

1.操作

单击菜单“工具”、“数据分析”，在弹出的数据分析窗口选择“描述”统计，如图2所示。

2.选项设置

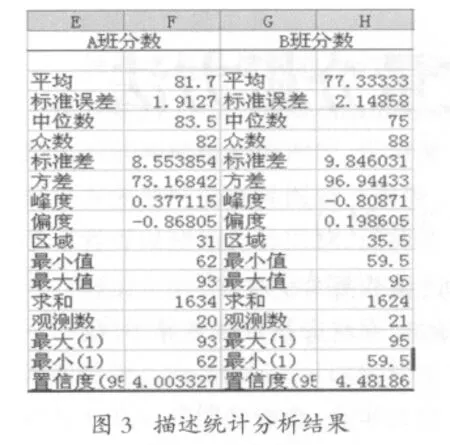
“输入区域”是待分析数据组所在单元格区域，A班分数位于B1:B21中，计算A班统计量应在“输入区域”中选B1:B21。由于待分析数据是按列分布的，“分组方式”选“逐列”。“输入区域”中第一个单元格B1显示“A班分数”是该列的变量名称，并非考试分数，所以要选上“标志位于第一行”。在“输出区域”中选入单元格E1，表示要把A班的描述统计分析结果放在E1开始的E列中。另外选上“汇总统计”、“平均数置信度”、“第K大值”、“第K小值”。“第K大值”后面的方框中填上“1”表示给出最大的“1”个数，即最高分，根据需要可以自行选填数字。设置完之后，按“确定”即可求出A班分数的描述统计量。按同样的操作方法可求出B班分数的统计量。

3.分析结果

Excel描述统计分析结果如图3所示，已求出考试分数的平均值、最大值、最小值、方差等基本统计量。

二、Excel直方图的使用

完成了第一项任务之后，下面使用Excel数据分析中的“直方图”，统计各个分数段的人数分布情况。

1.“接收区域”数据准备

在D2：D5中输入数值60、70、85、100。接收区域是数据分组的依据：“60”表示小于等于60的数组；“70”表示大于60小于等于70的数组；“85”表示大于70小于等于85的数组；100表示大于85小于等于100的数组。

2.操作

选“工具”/“数据分析”/“直方图”，弹出“直方图”窗口，如图4，进行相应选项的设置。大部分选项的含义与上述“描述统计”窗口一致，选上“累积百分率”、“图表输出”，按“确定”。对于B班分数采用同样的操作方法。

3.分析结果

输出结果如图5。由分析结果可知，A班分数没有60分以下的；大于60小于等于70有2人，占10%；70到85之间的有11人，占55%；85以上有7人，占35%。

三、T检验与F检验

下面采用T检验、F检验定量比较分析A班与B班分数的差异。先采用F检验判断A、B班考试分数是否等方差，然后采用T检验判断A、B班分数是否有显著差异。

1.F检验

选“工具”/“数据分析”/“F检验双样本方差”，如图6所示。“变量1的区域”方框中选上A班分数B1:B21，“变量2的区域”方框中选上B班分数C1:C22，选上“标志”，默认的α值（显著性水平）为0.05，“输出区域”选D1，按“确定”，得到F方差齐性检验的结果。

F检验结果：P(F<=f)单尾= 0.271753086>0.05，接受同方差假设，即认为两个班的考试分数方差是一致的。

2.T检验

选“数据分析”/“t-检验：双样本等方差假设”，如图7所示。与F检验一样，“变量1的区域”方框中选上A班分数B1:B21，“变量2的区域”方框中选上B班分数C1: C22，选上“标志”。“假设平均差”输入“0”，表示原假设认为两个班的分数不存在差异，即平均分之差为0。默认的α值为0.05，“输出区域”选D1，按“确定”，得到T检验结果。

T检验结果：

P(T<=t)双尾=0.138418242> 0.05，

t Stat=1.512698968，

t双尾临界=2.022690901，即接受原假设，认为A、B两班的考试分数差异在统计上不显著。

[1]沈浩，李亦兰，王迎迎.Excel高级应用与数据分析[M].北京：电子工业出版社，2008.

[2]贾俊平，何晓群，金勇进.统计学[M].北京：中国人民大学出版社，2000.

[3]吕红升.用Excel的数据分析工具分析试卷[J].巢湖学院学报，2004，(6).

（编辑：鲁利瑞）

TP311.56

B

1673-8454（2011）02-0057-02