L－V模型在软土地基沉降预测中的应用

张 雄，王金忠，赵凤岐，白金剑

(1.河北工程大学土木工程学院，河北邯郸056038;2.河北中金黄金有限公司，河北 石家庄050011)

事物的发生、发展、成熟然后达到一定极限的过程和软土地基在逐步施加荷载产生沉降趋于稳定的过程十分相似［1－3]，Logistic模型和 Von － Bertalanffy模型为非线性生长模型，在预测生物界成长规律中应用较为成熟［4]。把这两种模型应用到软土地基的沉降预测中来，能够较好地反映全过程的沉降量与时间的关系［5－7]，然而在预测沉降时还是存在一定的误差，预测精度不够高。本文提出Logistic－Von－Bertalanffy叠加模型(L－V模型)，并利用Origin软件求解模型参数，研究其在实际工程中的应用效果。

1 预测模型的建立

1.1 基本模型

Logistic模型又称泊松曲线模型，其表达式为

式中y—沉降量;t—时间;A—最终沉降量;k—瞬时沉降速率;B—待求参数。

Von－Bertalanffy模型表达式为

式中参数意义同Logistic模型。

1.2 L－V模型建立

为了进一步提高沉降预测精度，笔者将上述2种模型进行叠加，提出含有6个参数的L－V模型，其表达式为

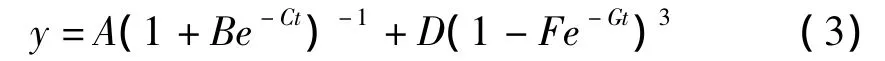
式中:A、B、C、D、F、G—待求参数。

在Origin软件中定义函数表达式、参数、变量，将观测数据导入软件中进行拟合，可以得到拟合曲线，以及回归方程的参数值。

当t=0时

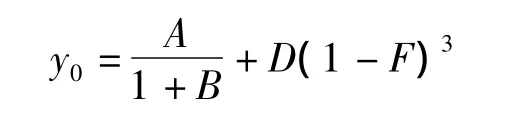
由于 A、B、D、F 不同时为零，所以 y0≠0，即曲线不过原点。对于饱和土，在荷载作用下地基发生瞬时沉降，在体积不变的情况下由剪应变引起沉降;对于非饱和土，施加荷载后，孔隙中气体被排除，土骨架发生变形，产生瞬时沉降。

当t→∞时

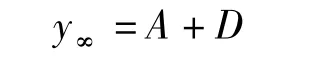
A+D为地基的最终沉降量，由A、D共同来反映，随着时间的增长沉降量必然趋近于一稳定值。

1.3 预测效果评价

如何评价预测结果的精度和可靠性是预测分析的重要组成部分，通常采用多项误差形式来对预测结果进行评价，以此来判定各种预测方法优劣或者一种预测方法的可行性［8]，本文拟采用绝对误差平方和SSE、均方根误差RMSE、相关系数平方R2等3个指标进行评价，公式如下:

2 案例分析

珠江三角洲某码头工程位于软土地区，地基土天然含水量高、抗剪强度低、压缩系数高，不能满足地基承载力和变形要求，需要进行人工处理加固，该工程采用真空联合堆载预压法。

2.1 全过程沉降预测分析

本文拟采用该工程第12号沉降观测孔铺设真空膜重埋沉降板后的88组观测数据，利用拟合软件得出C12孔沉降预测值，并绘制出L－V模型沉降量与时间关系曲线(图1)。

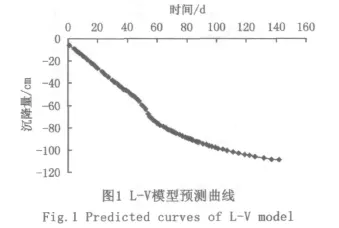
从图1可以看出，L－V模型预测曲线形状上呈反S形。在t=0时刻，模型的预测值不为零，反映了刚开始在软土地基上施加荷载时地基会产生初始沉降，这与实际情况相符;随后沉降进入主固结阶段，在t=50 d左右出现反弯点，反弯点之前沉降速率不断增加，反弯点之后沉降速率逐渐减小;图中t=100 d之后沉降量与时间关系曲线近似直线，主固结结束，沉降进入次固结阶段，地基土有效应力已基本不变，但土体体积仍随时间增长而发生压缩;t→∞时，软土地基沉降趋于一稳定值。

表1 3种模型预测效果Tab.1 Prediction results of 3 models

从表1可以看出软土地基全过程沉降预测的L－V模型相关系数平方R2最高，达到0.997 8，反映了L－V模型拟合程度最高;Logistic模型的SSE和RMSE最大，Von－Bertalanffy模型的SSE和RMSE次之，L－V模型的SSE和RMSE最小，表明L－V模型的精度较Logistic模型和Von－Bertalanffy模型要高。

2.2 沉降后期预测分析

由于上述3种模型在沉降前期预测误差较大，且实际工程中对前期沉降关注不高，故不作讨论。这里仅对沉降后期次固结阶段进行沉降预测分析，绘制沉降后期观测值与预测值曲线，如图2所示。

从图2可以看出沉降后期L－V模型预测值曲线与观测值曲线吻合度最高，经式(5)算得，LV模型均方根误差(RMSE=1.512)小于Logistic模型(RMSE=2.930)和 Von－Bertalanffy模型(RMSE=3.624)均方根误差，L－V模型的预测值相比Logistic模型和Von－Bertalanffy模型更接近实测值，并且预测值稍微比实测值偏大，实际工程中这对预测最终沉降、并采取有效控制措施很有帮助。

3 结语

工程实例表明，软土地基沉降的L－V模型相关系数平方R2=0.997 8，其拟合程度比单一的Logistic模型和Von－Bertalanffy模型的拟合程度要高;沉降观测后期L－V模型的均方根误差小于Logistic模型和Von－Bertalanffy模型的均方根误差，其预测值更加接近观测值，而实际工程中我们关注更多的正是后期沉降量，这对预测最终沉降提供了更高的可靠性。对于从理论角度阐述LV模型在与其他模型相比，其预测误差小、预测精度高等问题，还有待进一步研究。

［1] 宰金珉，梅国雄.成长曲线在地基沉降中的应用［J] .南京建筑工程学院学报，2000，53(2):8－13.

［2] 梅国雄，宰金珉，殷宗泽，等.沉降－时间曲线呈“S”型的证明—从一维固结理论角度［J] .岩土力学，2004，24(1):20 －22.

［3] 梅国雄，宰金珉，殷宗泽，等.沉降－时间曲线呈“S”型的证明—从土体本构关系［J] .岩土力学，2005，26(增1):21－24.

［4] 武海霞.基于冠层分析仪的冬小麦叶面积指数测算级模拟［J] .河北工程大学学报:自然科学版，2010，27(3):104－106.

［5] 宋宇鹏，徐贺文，孟伶俐.生长模型在地基沉降全过程预测中的应用［J] .铁道建筑，2006(3):62－64.

［6] 冯建光，于广云，刘 灿.超量塌陷区铁路桥结构的检测与评估［J] .黑龙江科技学院学报，2009，19(4):291－294.

［7] 赵明华，龙 照，皱新军.基于Logistic曲线和Gompertz曲线的最有组合沉降预测模型及其应用［J] .公路交通科技，2007，24(12):1 －4.

［8] 戴 钰.最优组合预测模型的构建及其应用研究［J] .经济数学，2010，27(1):92－98.