基于连体相对高度的双塔连体结构分析

郭远翔，陈康华

(1.华南理工大学土木与交通学院，广东广州，510640;2.华南理工大学建筑设计研究院，广东广州，510640)

根据塔楼结构布置的不同，双塔连体结构可分为对称双塔连体结构和非对称双塔连体结构两种。其中，非对称双塔连体结构的两塔楼的结构布置相异，其振动形式比对称双塔结构更为复杂。因此，对非对称双塔连体结构动力特性的研究具有重要意义。

1 对连体相对高度系数的定义

为了便于研究连体设置高度对非对称连体结构影响的一般规律，保持连体部分的结构布置与各塔楼的结构布置都不变，即连体部分的刚度与各塔楼刚度的比值保持不变，对连体设置高度进行无量纲化。将连体部分的结构顶面高度与连体相连接的较矮塔楼的结构顶面高度的比值定义为连体相对高度系数，如下式所示。

式中βc－连体相对高度系数;hc－连体部分的结构顶面高度;H－和连体相连接的较矮塔楼的结构顶面高度。

2 计算模型的建立

采用一非对称双塔连体结构进行结构模拟分析:13层框架结构，7度，设计基本地震加速度为0.10 g，柱网尺寸为9 m ×9 m，层高 4 m，Ⅱ类土，框架抗震等级为三级，连体跨度为18 m。混凝土强度等级为C30，钢筋级别为HRB400。较矮塔楼的柱截面尺寸为600 mm×600 mm，较高塔楼的柱截面尺寸为800 mm×800 mm，主梁及连体梁的截面尺寸为250 mm×800 mm，次梁的截面尺寸为200 mm×600 mm，楼板厚100 mm。使用结构分析设计系统MIDAS Building进行建模分析，图1为该结构三维模型。

3 自振模态及自振周期分析

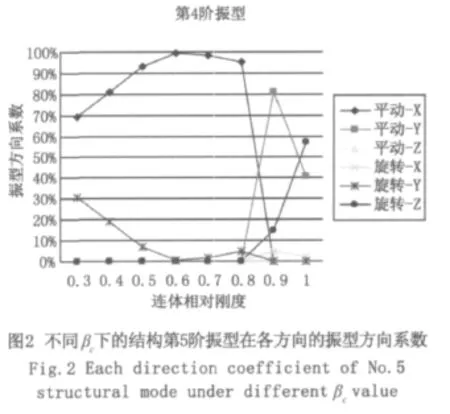
改变连体的设置高度，建立8个不同设置高度的模型，对其使用CQC法进行动力特性分析。由于非对称双塔连体结构的两塔楼刚度分布不一，故结构的各阶模态均为非对称振动模态。在结构的前10阶自振模态中，第5阶至第10阶振型皆因βc的改变而产生较大变化。其中，结构第5阶振型在各方向的振型方向系数随βc的变化如图2所示。

同样采用上述方法改变连体相对高度系数βc，对不同连体设置高度的8个算例进行计算。得到βc在0.3－1.0之间变化时该结构的前10阶自振周期如图3所示。

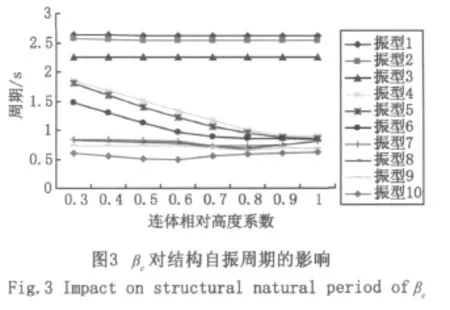
由以上分析可见:(1)连体相对高度系数的变化对结构的低阶自振模态产生较大影响。(2)在结构的第5阶振型中，无论βc如何变化，平动－Z、旋转－X方向的振型方向系数始终为0或接近于0。而随着βc的变化，平动－X、平动－Y、旋转－Y、旋转－Z方向的振型方向系数在0% －100%之间产生大幅度的跳跃。(3)随着βc的增大，结构的第 1、2、3、7、8、9、10 阶自振周期变化平缓，即受βc的影响不大。(4)随着βc的增大，结构的第4、5、6阶自振周期逐渐减小并趋于稳定，表现为结构整体刚度加大。

4 基底剪力及倾覆弯矩分析

结构的基底剪力及倾覆弯矩随βc的变化如图4所示。

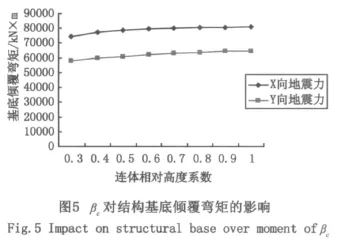
由图4及图5可见:(1)随着βc的改变，结构的基底剪力及倾覆弯矩变化平缓。不同的连体设置高度对结构的基底剪力及倾覆弯矩影响较小。(2)结构的基底剪力及倾覆弯矩随βc的加大而略显增大。因此，采用较小的连体设置高度可略减结构的基底剪力及倾覆弯矩。

5 结论

1)连体相对高度系数的变化可以在较大程度上改变结构的自振模态，对非对称双塔连体结构的低阶振型产生较大影响。

2)连体相对高度系数可使结构的自振周期产生显著变化，其总体变化趋势随着连体相对高度系数的增大而减小。

3)连体的介入使非对称双塔连体结构的平扭耦联程度增强。对该类结构进行动力特性分析时必须采用CQC法，同时必须考虑连体对结构的贡献，进行整体分析。

4)非对称双塔连体结构的基底剪力及倾覆弯矩受连体设置高度的影响较小，但较小的连体设置高度可适当减少结构的基底剪力及倾覆弯矩。

［1] GB50011－2010，建筑抗震设计规范［S] .

［2] 黄坤耀.双塔连体结构的静力、抗震和抗风分析［D] .杭州:浙江大学，2001.

［3] 包世华，王建东.大底盘多塔楼连体结构的受力分析［J] .建筑结构，1996(11):7 －13.

［4] 卞朝东，李爱群，娄 宇，等.高层连体结构振型及其参与系数的分析［J] .建筑科学，2002，18(4):20 －24.

［5] 刘晶波，李征宇，石 萌，等.大跨高层连接体建筑结构动力分析［J] .建筑结构学报，2004，25(1):45 －52.

［6] 焦柯，李松柏，陈润辉.东莞海德广场双塔连体高层结构动力弹塑性分析［J] .建筑结构，2009，39(8):17－98.