基于改进蚁群算法的钢管混凝土构件的优化

周书敬，潘靖

(河北工程大学土木工程学院，河北邯郸056038)

钢管混凝土结构因其具有施工周期短，经济效果好及承载力高等诸多优点，在高层建筑中的应用日渐广泛。目前对于钢管混凝土结构的研究大多集中在结构的基本性能和计算理论方面，陈云波等［1]对钢管混凝土柱的构造和火灾后的承载力进行了研究;黑文豪等［2]利用有限元分析软件ANSYS并采用剥离钢管与混凝土的方法，对圆钢管混凝土轴压短柱的极限承载力进行了研究;周绪红等［3]通过4个圆钢管约束混凝土和4个方钢管约束混凝土压弯构件的试验，研究了钢管混凝土构件的界面特征对滞回性能的影响。然而，对于钢管混凝土构件优化方面的研究目前并不多见，只有王海军等［4]曾利用MATLAB遗传算法工具箱建立钢管混凝土构件的优化模型，通过计算分析构件的模态，获得了构件优化后的内力和经济指标。本文通过挥发系数的改进，将改进后的蚁群算法应用到钢管混凝土构件的优化中，建立构件优化模型，并通过算例与文献［4] 的构件优化进行比较。

1 基本蚁群算法的优化机理

蚁群算法(Ant Colony Algorithm，ACA)是意大利学者 M.Dorigo，V.Maniezzo和 A.Colorni受到自然界中蚂蚁的觅食过程启发利用计算机仿真实验提出的一种自适应正反馈的模拟进化算法［5－7]。算法的核心是与信息素浓度相关动态参数的设定和控制［8－9]。

假设存在n个城市的集合C={C1，C2，…，Cn}，城市i和j之间的距离为 dij，设存在 m只蚂蚁，t时刻蚂蚁留在城市i的数目为bi(t)(t)。t时刻路径(i，j)上残留的信息素量用τij(t)表示，位于城市i的蚂蚁k根据路径上呈现动态变化的 τij(T)，依概率(t)选择路径(i，j)，则

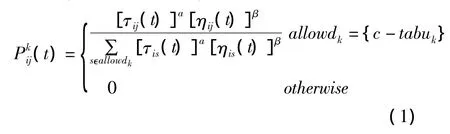
式中tabuk(k=1，2，…，m)—禁忌表，表示蚂蚁k当前所经过的城市;allowdk—蚂蚁k当前允许选择的城市;α、β—信息素和期望值的权重。

当m只蚂蚁完成一次循环后，各路径上的信息素更新如下:

其中Q—蚂蚁在本次循环中所释放信息素的总和;Lk—第k只蚂蚁在本次循环中所走过的路程;—第k只蚂蚁在经过本循环的路径(i，j)上所遗留的信息素;Δτij(t)—路径(i，j)上增加的信息素量;ρ—信息素挥发系数，ρ∈［0，1] 。

2 改进后的蚁群算法

2.1 蚁群算法的改进

蚁群算法在运用过程中，完成一次循环后，必定会产生一些可行解和劣质解，并且会出现算法收敛慢和容易陷于局部最优的现象，这对我们在合理的迭代次数下获得问题的最优解是不利的，而信息素挥发系数的大小对于蚁群算法的收敛性和全局搜索能力影响有直接的影响。鉴于此，本文对蚁群算法中的信息素更新策略进行改进，自适应地调整挥发系数ρ。首先赋予ρ一个较大的初始值，使得算法在前期进行较优路径的搜寻;后期通过逐渐调小ρ的方法以扩大搜索空间避免陷入局优。当算法似乎陷入局优时，ρ采用以下公式进行自调整［10]:

其中ρmin—ρ的最小值。

信息素的更新策略上采用全局更新以提高算法的收敛速度:

其中Lmin—蚂蚁本次循环中经过城市i和j的最短路径的边。

改进蚁群算法的流程如下:首先初始化参数，设定最大循环次数NCmax，将m只蚂蚁随机放在n个节点。如果循环次数NC≥NCmax，直接输出打印结果，否则，每只蚂蚁根据状态转移公式(6)依概率进行转移，随后修改禁忌表。m只蚂蚁遍历一周后，本次循环的最短路径记为Lmin，将第一次得到的最优路径记为Lg。所有蚂蚁遍历完城市后，按照式(2)、式(3)、式(6)更新全局信息素和最优路径表。将Lmin和Lg进行比较，若Lmin＜Lg，则令Lg=Lmin;若 Lmin＞ Lg，则令 NC=NC+1，循环到最短路径并打印输出结果。改进蚁群算法的流程图见图1。

2.2 矩形钢管混凝土构件的优化

(1)设计变量:对于矩形钢管混凝土梁柱结构来说，柱子以其外径D1、钢管的壁厚T1为设计变量，梁以其长径D2、钢管的壁厚T2和梁宽B为设计变量。

(2)目标函数的建立［11]

柱:

梁:

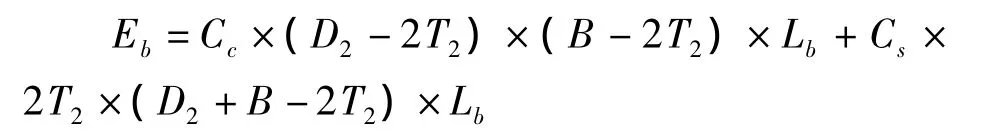
其中:Ez、Eb—柱、梁的造价;Cc—混凝土单位体积造价;Cs—钢材单位体积造价;Lz—柱的长度;Lb—梁的长度。

套用定额［12]，则 Cc=470 元/m3，Cs=56 991元/m3，Lz=360 mm，Lb=1 000 mm

(3)约束条件

①柱:

a强度承载力:N≤Nu

其中:N、Nu—各荷载作用下的最不利轴力和极限轴力

b变量范围:D≥100，T≥4

c 含钢率:0.1≤a≤0.7

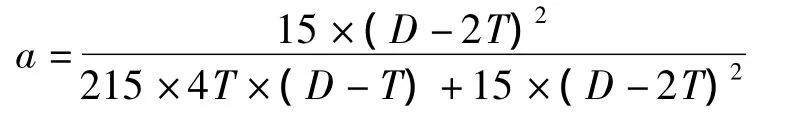
②梁:

a稳定性:M≤Mu

其中M、Mu—各荷载作用下的最不利弯矩和极限弯矩。

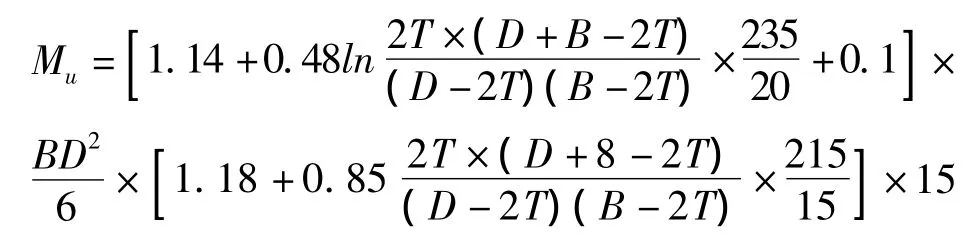
b变量范围:B≤100，T≥4

c 含钢率:0.1≤a≤0.7

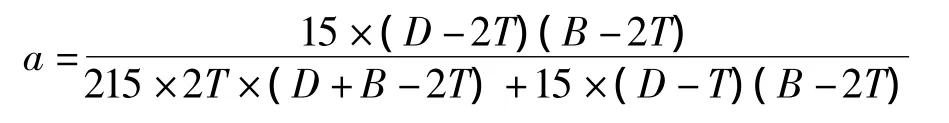
(4)优化模型的简单描述

设计变量x

式中g(x)—约束函数;D—一个集合，集合中的元素是有限个点。

2.3 求解

将m只蚂蚁随机放到n个节点上，采用式(2)、式(3)、式(6)进行信息素和最优路径的更新，将目标函数(经济指标)看作是蚂蚁经过的路径总长，则本文的优化问题就转变为蚂蚁在最佳路径上寻得食物问题。最后应用MATLAB语言编写程序，采用ANSYS10.0对结果进行分析。

3 算例分析

选自文献［13] 中的试验构件，柱子:D×T×L=120 mm×5 mm×360 mm，承受轴向力最大值为700 kN;梁:D×B×T×L=150 mm×120 mm×5 mm×1 000 mm，承受弯矩最大值为29(kN·m)，梁柱构件的材料相同，混凝土标号C30，钢管采用Q235钢板，优化的目标函数选取经济指标(最低)，从而提高建筑的经济性。构件设计变量的优化结果见表1。

控制参数取值如下:城市n=51，蚂蚁数m=20，a=2，β =5 ，初始 ρ=0.9，ρmin=0.1。Q=150梁柱迭代次数的关系曲线如图2所示。

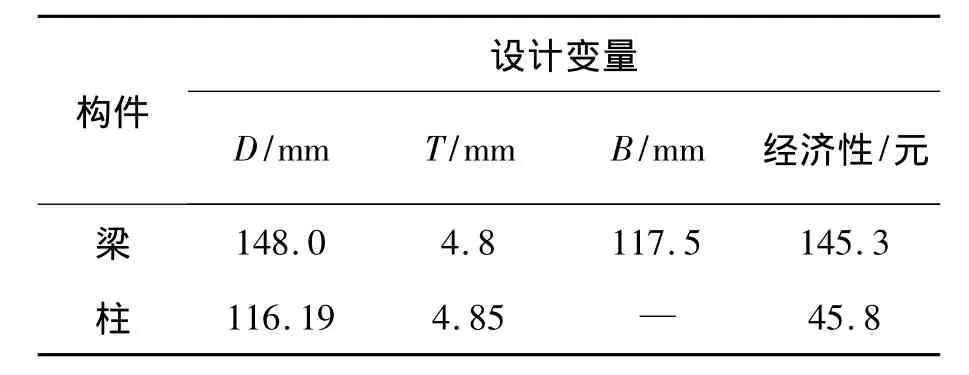
表1 构件设计变量的输出结果Tab.1 The results of member’s design parameter

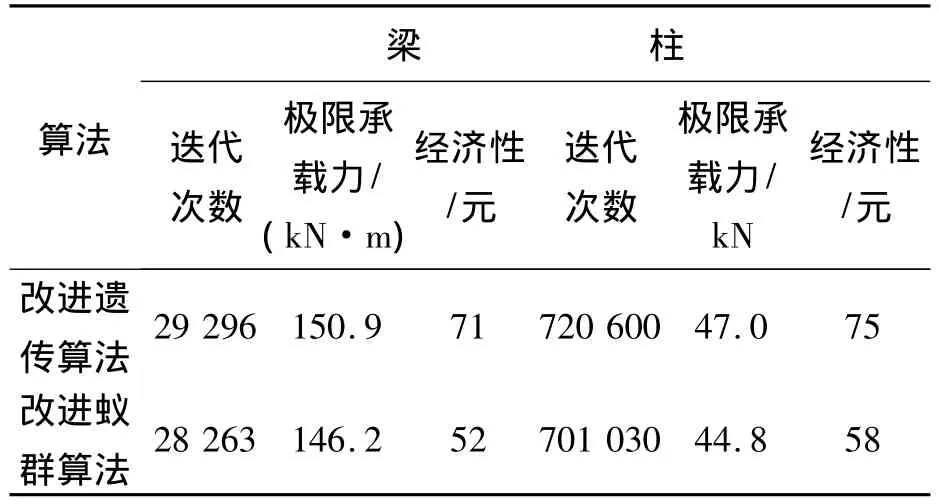
表2 改进蚁群算法与改进遗传算法的优化结果比较Tab.2 The comparison of optimization’s results between the improved ACA and GA

由表1可以看出，与文献［13] 中梁柱的截面尺寸相比，通过改进的算法优化后相对应的设计变量在尺寸方面都得到了优化。将改进蚁群算法的优化结果与文献［4] 利用改进遗传算法对钢管混凝土构件的优化结果进行了比较(表2)，同样可以看出，在梁柱优化前后的承载力相差不大的情况下，且承载为大于实际所承受的轴力与弯矩时，迭代次数有所减少。相比之下，柱在优化后，经济性节省了4.7%，梁在优化后节省了3.1%。从图2可以看出改进后的算法可以得到全局最优解，优化效果明显，适用于钢管混凝土构件的优化。

4 结论

1)信息素全局更新策略对挥发系数的调整，很好地弥补了蚁群算法收敛速度慢和容易陷入局部最优解的不足。

2)在承载力优化前后相差不大且符合设计要求的前提下，改进后的蚁群算法经过更少的迭代次数，求得了更小的目标函数值，达到了梁柱构件造价最低的目的。

［1] 陈云波，韩金生.钢管钢筋混凝土柱的研究［J] .山东科技大学学报:自然科学版，2010，29(2):30－34.

［2] 黑文豪，许波.基于ANSYS的圆钢管混凝土轴压短柱极限承载力分析［J] .广东建材，2010(4):7－9.

［3] 周绪红，张素梅，刘界鹏.钢管约束钢筋混凝土压弯构件滞回性能试验研究与分析［J] .建筑结构学报，2008，29(5):75 －84.

［4] 王海军，金勇，李兴权，等.基于遗传算法的钢管砼构件的优化［J] .科技信息，2009(7):14－15.

［5] 周书敬，吴 超.房地产投资环境的模糊多群体准则评价方法［J] .河北工程大学学报:自然科学版，2007，24(3):68－71.

［6] 史三元，侯桂欣，苏晓亮.小高层钢结构住宅抗震性能研究［J] .河北工程大学学报:自然科学版，2010，27(2):1－4.

［7] DORIGO M，MANIEZZO V，CONORNI A.Ant system:optimization by a colony of cooperating agents［J] .IEEE Transactions on Systems，Man，and Cybernetics，1996，26(1):29－41.

［8] 段海滨.蚁群算法原理及其应用［M] .北京:科学技术出版社，2005.

［9] 崔之熠，王茂芝，刘国涛，等.蚂蚁算法在TSP问题求解的应用［J] .四川理工学院学报:自然科学版，2011，24(3):334－337.

［10] DJB 15－31－2003.钢管混凝土结构技术规程［S] .

［11] GB 50017－2003.钢结构设计规范［S] .

［12] 鄂建文［2008] 216号文.湖北省建筑安装工程费用定额［Z] .

［13] 韩林海.钢管混凝土结构［M] .北京:科学出版社，2007.