一类半无限极大极小问题的神经网络

杨红梅 张自武 马园媛 孙 隆

(1，2 ，3 .昌吉学院数学系 新疆 昌吉 831100；4.西南大学经济管理学院 重庆 400715)

半无限规划问题最早出现于20世纪60年代，其早期理论主要由Charnes等人创立。Kortank、Lopez和Polak等人在这方面也作了大量工作。作为数学规划的一个重要分支，其研究引起了国内外学者的广泛关注，现已成为数学规划的一个重要研究方向。它不仅在经济领域、最优控制、信息技术及计算机网络，而且在工程技术、机器人路径设计等方面都有广泛而直接的应用。而半无限极大极小问题是一类重要的半无限规划问题，因此研究半无限极大极小问题有重要的现实意义。

引言

考虑带线性等式约束的半无限极大极小问题，其一般形式为

其中ψi(x)(i∈I)是连续可微的凸函数，x=(x1,x2,...,xn)T∈Rn，I为无限集，A∈Rm×n(m≤n),b∈Rm。

在该问题中，可以看出它的约束条件的个数是无限的，在求解方面存在一定难度，所以有必要寻找求解它的新方法。而神经网络具有高速并行计算能力，能够硬件实现，因此它是实时求解高维的复杂的最优化问题的一条非常有效的途径。此外神经网络的稳定性、有效性和全局收敛性等方面都比传统优化方法更优越。近几年来，利用神经网络求解最优化问题，已经有了很多的运用，而且它们的计算效果都很好[1-6]。根据上述考虑，为实时并行求解问题(1),本文根据它的结构特点，构造了求解它的一个神经网络，严格说明了该模型是Lyapunov稳定的，并收敛于问题(1)的精确解。为叙述方便， 标记e=(1,0,0,...,0)∈Rn。

定义 若神经网络所对应的动力系统分别是Lyapunov稳定和渐近稳定时，则称该网络分别是Lyapunov稳定和渐近稳定的。

定理1(射影定理)[7]设v∈Rn为一个闭凸集，F是从Rn到自身的一个单调算子，求一个向量u*∈v，使得

F(u*)T(u-u*)≥0, ∀u∈v，VI(v,F)

那么，u*是VI(v,F)的解当且仅当u*是射影方程u=Pv(u-F(u))的解。

为求解问题(1),作如下假设：问题(1)存在有限解x*∈Rn。

1 构造神经网络模型

首先问题(1)等价于下面的非线性规划问题

其中x=(x1,x2,...,xn)T∈Rn。显然问题(1)的最优解的获得可以通过求解问题(2)的最优解。

在问题(2)中，其不等式约束条件的个数是无限多的。可以从文献[8]中知：当所考虑问题是凸规划时，可用问题(3)来逼近问题(2)，也就是通过求解问题(3)来获得问题(2)的最优解，即：

此外问题(3)有有限最优解且满足slater's条件[9]. Ω-ψi(x)在Rn上是连续可微凹函数，由凸规划的Kuhn-Tucker条件可以得到下述结论：

定理2x*是(3)的最优解，当且仅当存在λ*∈Rl，μ*∈Rm，使下式成立

证明：显然问题(3)的拉格朗日函数为

L(x,λ,μ)=Ω-λT(Ω-ψi(x))-μT(Ax-b)

它是定义在C=Rn×Rl×Rm.

由于问题(3)是凸的，且满足Slater条件，根据凸规划KKT条件知：x*是问题(3)的最优解，当且仅当存在λ*∈Rl,μ*∈Rm，使得(x*,λ*,μ*)是L(x,λ,μ)在C上的鞍点，即

L(x*,λ*,μ)≤L(x*,λ*,μ*)≤L(x,λ*,μ*)，∀(x,λ,μ)∈C(5)

由(5)式左边得：

(λ-λ*)(Ω-ψi(x))-(μ-μ*)(Ax*-b)≤0,∀(λ,μ)∈Rl×Rm,

进而对∀(λ,μ)∈Rl×Rm，有：

Ax*=b,λ*≥0,Ω-ψi(x)≥0,(λ*)T(Ω-ψi(x))=0.

再对∀x∈Rn,且x≠x*，可知x*+t(x-x*)∈Rn,∀t∈(0,1)，那么由(5)式右边得

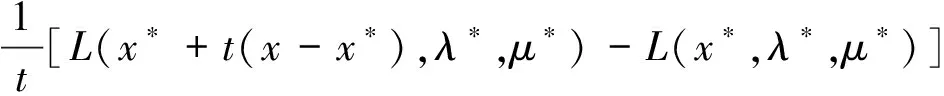
令t→0，并取极限，就有

(x-x*)TxL(x*,λ*,μ*)=(x-x*)T[e-(e-ψ'i(x*))Tλ*-ATμ*]≥0，∀x∈Rn.

再结合定理1知：

定理3[10]x*是问题(3)的最优解当且仅当存在λ*∈Rl，μ*∈Rm，使得

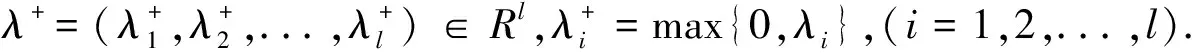
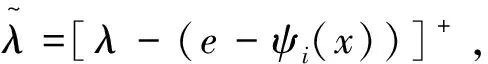
其中k>0是设计参数。

再根据定理3和 (7) 式可以得到动力系统(6)的解和神经网络(7)的平衡点两者之间的关系。

推论1 设C*={z∈Rn+l+m|z是系统(6)的解}，则z∈c*当且仅当z是神经网络(7)的平衡点。

2 稳定性分析

首先讨论神经网络(7)初值问题解的存在惟一性，再给出它的稳定性定理。类似于文献[10]中的证明，可得出下述结论。

定理4[11]若e-ψi'(x)(i=1,2,...,l)在Rn上局部Lipschitz连续，则对任意的z0∈Rn+l+m，神经网络(7)在[0,+∞)上存在惟一的以z0为初值的连续解z(t)(z(t0)=z0,∀t≥t0)。

定理5[12]若e-ψi'(x)(i=1,2,...,l)在Rn上局部Lipschitz连续，则神经网络(7)是Lyapunov稳定的。特别地，若C*={z*}，则神经网络(7)全局渐近稳定。

参考文献：

[1] Y.S.Xia, J.Wang. A general methodology for designing globally convergent optimizationneural networks[J]. IEEE Tran. on Neural Networks,1998,9:1311-1343.

[2] Y.S.Xia. A new neural network for solving linear programming and quadratic programming problem[J]. IEEE Trans. on Neural Networks,1996,7:1544-1547.

[3] A Bouzerdorm, T R Pattison. Neural Network for quadratic optimization with bound constrains[J]. IEEE Tran. on Neural Networks,1993,4:293-304.

[4] Gao Xingbao. A neural network for a class of extended linear variational inequalities[J]. Chinese Journal of Electronics,2001,10(4):471-475.

[5]杨红梅等.解一类非线性极大极小问题的神经网络[J].陕西科技大学学报，2006，24(4)：90-94.

[6] 杨红梅.求解凸不等式组问题的神经网络方法[J].昌吉学院学报，2009，(3)：95-97.

[7] D Kinderlehrer，G Stampacchia. An introduction to variational inequalities and their applications[M]. New York: Acadimic,1980.

[8] 李师正.半无限规划的鞍点与对偶性[J].数学物理学报.1996，16(2)：174-178.

[9] M. Avriel, Nonlinear Programming: Analysis and Method.Englewood Cliffs, NJ: Prentice-Hall,1976.

[10] [11] [12] X..B.Gao, L.-Z.Liao, L.Q.Qi. A novel neural network for variational inequalities with linear and nonlinear constraints[J]. IEEE Trans. Neural Network, 2005,16(6):1305-1317.