谈谈有向图的一个应用
—— 求网络最大流问题
2011-10-13周承贵
周承贵
(桂林理工大学南宁分校,广西 南宁 530001)
谈谈有向图的一个应用
—— 求网络最大流问题
周承贵
(桂林理工大学南宁分校,广西 南宁 530001)
网络最大流是一类应用很广泛的问题,有十分重要的现实意义,本文给出一种求网络最大流的有效快捷的算法,此算法使计算网络最大流变得简便且具有很强的实用性。
源汇;增广链;最大流
1 引言
图论中讨论的网络最大流是一类应用十分广泛的问题。比如现实生活中的交通系统中有人流、车流、货物流等;金融系统中有现金流;通信系统中有信息流;供水(油)系统中有水(油)流等,解决这类系统优化问题有十分重要的现实意义。
2 基本概念
[定义1]在有向图(网络图)中,只有流出量而没有流入量的顶点称为源;只有流入量而没有流出量的顶点称为汇;既有流入量也有流出量的顶点称为中间点;图中每一条弧一般都标注有两个权数(Cij,fij),其中前一个权Cij表示这条弧能容纳的最大流量,称为弧的容量,后一个权数fij表示该条弧现有的流量,称为弧的现有流量。若现有流量等于弧的容量,则称该弧为饱和弧,否则称不饱和弧。特别地,若弧的现有流量为0,则称该弧为零流弧,否则称非零流弧。
[定义2]若在一个网络图中每一条弧满足0≤fij≤Cij且中间点的流入量和流出量相等,同时源的流出量和汇的流入量也相等,则称网络图存在可行流。
所谓最大流问题就是在网络图中寻找流量最大的可行流。
3 网络最大流的求法
3.1 增广链的定义
[定义3]设f是一个可行流,若A是从VS到Vt的一条增广链,则A应该满足以下条件:①与前进方向一致的弧(称前向弧,记作A+)为非饱和弧;②与前进方向相反的弧(称后向弧,记作A-)为非零流弧。
求网络最大流的思想是通过标号法寻找从源到汇是否有流量可以增加的增广链,如有增广链,则调整增广链上弧的流量,来获取流值的更大流,直到找到最大流为止。
3.2 具体操作方法
(1)对具有可行流f的网络图,寻找一条由VS到Vt的增广链,直到找到为止;若不存在VS到Vt的增广链,则最大可行流为f。
(2)在所找到的增广链取调整流量值θ=min{(cij-fij)A+,(fij)A-}。
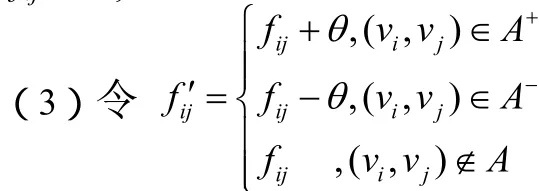
(4)对新可行流重复(1)到(3)过程,当再也找不到新的增广链时,此时源的流出量(或汇的流入量)就是网络图的最大流。
4 应用举例
求如图1所示输油管道网从vs到vt的最大流。

图1
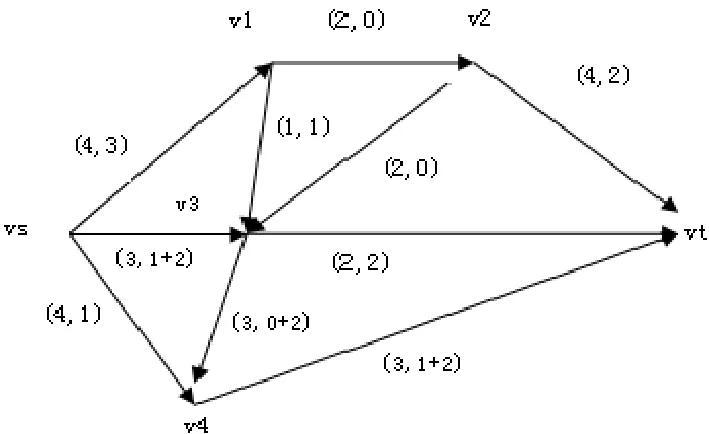
图2
略解:第一条增广链为:vs→v3→v4→vt,流量调整值为:θ1=min{2,3,2}=2,调整流量得图2。
第二条增广链为:vs→v1→v2→vt,流量调整值为:θ2=min{1,2,2}=1,调整流量得图3。
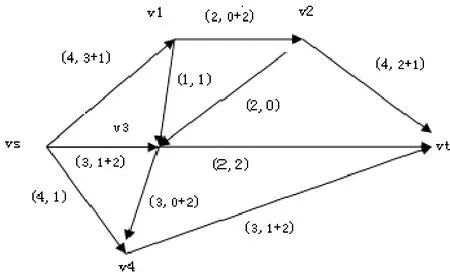
图3
在图3中再也找不到增广链,因此这时源的流出量就是输油管道网的最大流,且易求得管道的最大流为8。
5 结束语
使用上面的算法计算网络最大流的问题能使问题的解决变得简便易行,具有很强的实用性。
1 赵树利.计算机数学基础[M].北京:高等教育出版社,2004.2 2 云连英.工程应用数学[M].北京:高等教育出版社,2000.4 3 张忠志.离散数学[M].北京:高等教育出版社,2004.2
4 CEAC信息化培训认证管理办公室编.计算机数学基础[M].北京:高等教育出版社,2006.2
Chats the Oriented Graph an Application——Asks the Network Maximal-flow Problem
Zhou Chenggui
The network maximal-flow is a kind of application very widespread question, has the very vital practical significance, this article gives one kind to ask network most the big class the effective quick algorithm, this algorithm causes the computing network to change most greatly easily, and has the very strong usability.
the source collects; augments the chain; maximal-flow
O157.5
A
1000-8136(2011)06-0133-02
