拉格朗日中值定理的基本证法及应用小结

夏绿玉

（铜陵职业技术学院，安徽铜陵244000）

拉格朗日中值定理的基本证法及应用小结

夏绿玉

（铜陵职业技术学院，安徽铜陵244000）

拉格朗日中值定理是几个中值定理中最重要的一个，是微分学应用的桥梁，在高等数学的一些理论推导中起着很重要的作用。文章通过介绍几种不同构造函数的方法证明拉格朗日中值定理，并讲解拉格朗日定理的在不等式证明中的简单运用。阐述构造函数的方法和运用拉格朗日跳跃证明不等式的方法。

拉格朗日中值定理；罗尔定理；不等式

拉格朗日中值定理是高等数学的基础知识，它的证明过程中渗透的构造函数思想可以训练逻辑思维能力和解决问题能力。本文通过对定理证明过程的小结说明类比、构造的数学思想；通过对不等式证明的讲解，体现跳跃证明不等式的方法。首先讲一下罗尔中值定理拉格朗日中值定理及其几何意义。

一、定理证明

1.罗尔（Rolle）中值定理

如果函数f（x）满足条件：（1）在闭区间[a,b]上连续；（2）在开区间（a,b）内可导；（3）f（a）=f（b）则在（a,b）内至少存在一点ζ,使得f'（ζ）=0。

罗尔中值定理的几何意义：如果连续光滑曲线y=f（x）在点A、B处的纵坐标相等，那么，在弧上至少有一点C（ζ，f（ζ）），曲线在C点的切线平行于x轴，如图1。

注意定理中三个条件缺少其中任何一个，定理的结论将不一定成立；但不能认为定理条件不全具备，就一定不存在属于（a,b）的ζ，使得f'（ζ）=0。这就是说定理的条件是充分的，但非必要的。

2.拉格朗日（lagrange）中值定理

若函数f（x）满足如下条件：（1）在闭区间[a，b]上连续；（2）在开区间（a,b）内可导；则在（a,b）内至少存在一点ζ，使f'

拉格朗日中值定理的几何意义：函数y=f（x）在区间[a,b]上的图形是连续光滑曲线弧AB上至少有一点C，曲线在C点的切线平行于弦。如图2。

图二

从拉格朗日中值定理的条件与结论可见，若f（x）在闭区间[a,b]两端点的函数值相等，即f（a）=f（b），则拉格朗日中值定理就是罗尔中值定理。换句话说，罗尔中值定理是拉格朗日中值定理的一个特殊情形。正因为如此，我们只需对函数f（x）作适当变形，便可借助罗尔中值定理导出拉格朗日中值定理。

3.证明拉格朗日中值定理

（1）教材证法

显然，函数F（x）满足在闭区间[a,b]上连续，在开区间（a,b）内可导，而且F（a）=F（b）.于是由罗尔中值定理知道，至少存在一点ζ（a＜ζ＜b），

即f'

（2）用作差法引入辅助函数法

显然，函数φ（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，φ（a）=φ（b）=0，因此，由罗尔中值定理得，至少存在一点ζ∈（a，b），

（3）用迭加法引入辅助函数法

让f（x）迭加一个含待定系数的一次函数y=kx+m，例如令φ（x）=f（x）-（kx+m）或φ（x）=-f（x）+kx+m，通过使φ（a）=φ（b），确定出k,m，即可得到所需的辅助函数。

例如由φ（x）=f（x）-（kx+m），令φ（a）=φ（b）

得f（a）-（ka+m）=f（b）-（kb+m），从而，而m可取任意实数，这样我们就得到了辅助函数-x-m，由m的任意性易知迭加法可构造出无数个辅助函数，这些函数都可用于证明拉格朗日中值定理。

二、拉格朗日定理证明应用

拉格朗日定理是导数应用理论的基础，应用广泛。下面我们讨论它在不等式证明上的应用。证明不等式都是先找到一个函数，在闭区间上运用拉格朗日中值定理，再通过一定的放缩比较，得到结论。

例1证明对一切h＞-1，h≠0成立，不等式：

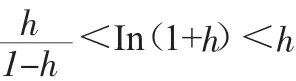
证明：设f（x）=In（1+x），则

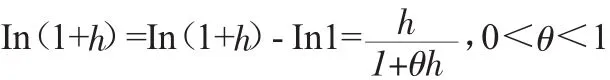
当h＞0时，由0＜θ＜1可推知

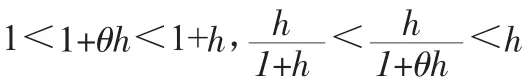
当-1＜h＜0时，由0＜θ＜1可推得

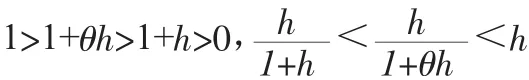
从而得到事实所要证明的结论。

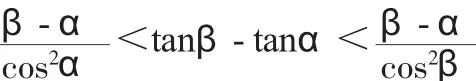
证明：在区间[α，β]上对函数tanx使用中值定理，可知存在ξ∈（α，β），使得

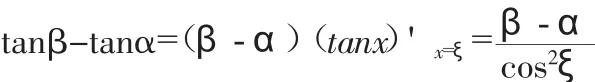
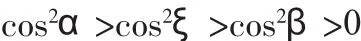
例3设f（x）在f'（x）上[a，b]连续，f'（x）在（a，b）内存在，若f（a）=f（b）=0，且有c∈（a，b）使得f（c）＜0，证明存在ξ∈（a，b）使得f'（ξ）＞0。

证明：分别在[a，c]，[c，b]上用中值定理有

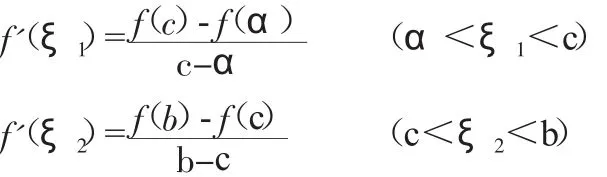
从而f'（ξ1）＜0，f'（ξ2）＞0在[ξ1，ξ2]再用中值定理，得

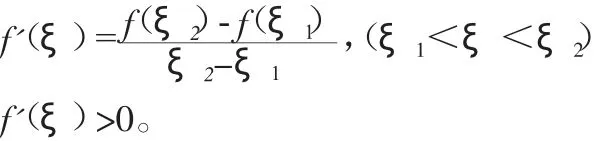
[1]华东师范大学数学系.数学分析[M].北京：高等教育出版社，2001.

[2]常庚哲，史济怀，等.数学分析教程[M].北京：高等教育出版社，2003.

[3]陈如邦，等.高等数学[M].北京：高等教育出版社，2009.

（责任编辑：王朝勇）

O172.1

A

1671-752X(2011)01-0093-02

2010-12-18

夏绿玉（1983-），女，安徽铜陵人，铜陵职业技术学院基础部教师，硕士在读，研究方向：概率论与数理统计。